Всюду в статье (если не сказано иначе) все группы – абелевы, А и В – бесконечные циклические группы, 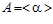 и
и 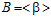 , п – целое положительное число, n > 1.
, п – целое положительное число, n > 1.
Определение 1. Подгруппа G прямого произведения 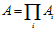 абелевых групп называется подпрямой суммой групп Аi, если для каждого i отображение
абелевых групп называется подпрямой суммой групп Аi, если для каждого i отображение 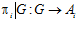 является эпиморфизмом, где
является эпиморфизмом, где 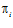 – проекция прямого произведения А на прямой сомножитель Аi. [4]
– проекция прямого произведения А на прямой сомножитель Аi. [4]
Как установлено [4], для того чтобы группа G являлась подпрямой суммой групп А и В необходимо и достаточно, чтобы существовали группа F и такие эпиморфизмы 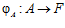 и
и 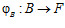 , что для любых элементов
, что для любых элементов 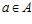 и
и 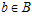 ,
, 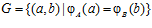 . Назовем F порождающей группой для подпрямой суммы G групп А и В, а эпиморфизмы
. Назовем F порождающей группой для подпрямой суммы G групп А и В, а эпиморфизмы 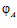 и
и 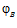 назовем определяющими для группы G.
назовем определяющими для группы G.
Определение 2. Если для некоторого данного числа 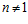 , группа G является подпрямой суммой данных групп А и В, порожденной конечной циклической группой Zп – аддитивной группой кольца вычетов по модулю п – то группу G будем называть элементарной специальной п-группой (esп-группой). В случае, когда число п неизвестно или может быть любым, такую группу мы будем называть es-группой.
, группа G является подпрямой суммой данных групп А и В, порожденной конечной циклической группой Zп – аддитивной группой кольца вычетов по модулю п – то группу G будем называть элементарной специальной п-группой (esп-группой). В случае, когда число п неизвестно или может быть любым, такую группу мы будем называть es-группой.
В данной статье продолжено изучение свойств esn-групп в зависимости от числа п, а также множества G всех es-групп. Ранее были доказаны ([2], [3], [8]) следующие утверждения, используемые в данной статье:
ТЕОРЕМА А. Для любого целого положительного числа 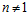 , существует взаимно-однозначное соответствие f между множеством элементарных специальных групп, индуцированных группой Zп,
, существует взаимно-однозначное соответствие f между множеством элементарных специальных групп, индуцированных группой Zп,
и мультипликативной группой обратимых элементов кольца вычетов по модулю п.
ТЕОРЕМА Б. Пусть G – esn-группа,  . Тогда,
. Тогда, 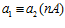 <=>
<=> 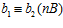 .
.
ТЕОРЕМА В. Пусть  и
и 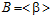 ,
, 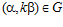 , где G – esn-группа, k – взаимно простое с п целое число,
, где G – esn-группа, k – взаимно простое с п целое число, 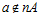 и
и 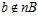 . Тогда,
. Тогда, 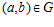 <=> существуют целые числа t и s такие, что
<=> существуют целые числа t и s такие, что 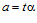 ,
, 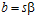 , и
, и 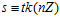 , и такие , что п не является их делителем.
, и такие , что п не является их делителем.
В данной статье доказывается следующее основное утверждение для класса esп-групп:
— esn-группа G, является подгруппой esn’-группы G’ <=> 1) 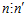 ; 2)
; 2) 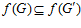 .
.
— группа G максимальна во множестве G <=> G – esp-группа для простого числа p. Минимальной es-группы во множестве G не существует.
Необходимые определения и обозначения приведены в работах [1] – [8].
ТЕОРЕМА I. Пусть G – esn-группа с парой определяющих эпиморфизмов 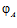 ,
, 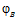 и G’ – esn’-группа с парой определяющих эпиморфизмов
и G’ – esn’-группа с парой определяющих эпиморфизмов 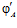 ,
, 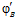 .
.
Тогда 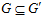 <=> для любых элементов а группы А, не принадлежащего подгруппе пА, и b группы В, не принадлежащего подгруппе пВ, выполняется условие:
<=> для любых элементов а группы А, не принадлежащего подгруппе пА, и b группы В, не принадлежащего подгруппе пВ, выполняется условие:
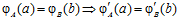 .
.
Доказательство непосредственно следует из определения esn-группы.
ТЕОРЕМА II. Пусть G – esn-группа и G’ – esn’-группа, 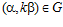 ,
, 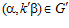 , где k – целое число, принадлежащее интервалу от 1 до n, k’ – целое число, принадлежащее интервалу от 1 до n’.
, где k – целое число, принадлежащее интервалу от 1 до n, k’ – целое число, принадлежащее интервалу от 1 до n’.
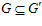 <=> 1)
<=> 1) 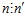 ; 2)
; 2) 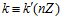 .
.
Доказательство. Пусть 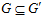 , тогда одновременно
, тогда одновременно 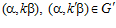 . Следовательно, по теореме Б,
. Следовательно, по теореме Б, 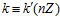 . С другой стороны, по теореме В, для любых целых чисел t и s, не делящихся на п, имеет место следующее условие:
. С другой стороны, по теореме В, для любых целых чисел t и s, не делящихся на п, имеет место следующее условие:
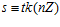 =>
=>
для чисел t и s взаимно простых с числом п’. Следовательно, очевидно, 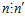 .
.
Обратно. Пусть 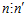 ,
, 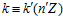 ,
, 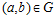 . Тогда, если
. Тогда, если 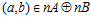 , то, очевидно,
, то, очевидно, 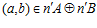 . Если же
. Если же 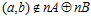 , то, по теореме В, существуют целые числа t и s, взаимно простые с числом п, такие, что
, то, по теореме В, существуют целые числа t и s, взаимно простые с числом п, такие, что 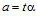 ,
,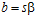 и
и 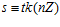 . Тогда
. Тогда 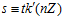 и, следовательно,
и, следовательно, 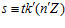 . Отсюда, по теореме В, следует, что
. Отсюда, по теореме В, следует, что 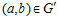 .
.
СЛЕДСТВИЕ 1. Пусть G – esn-группа. Тогда существует esn-группа – подгруппа группы G.
Доказательство, очевидно, непосредственно следует из теоремы II.
СЛЕДСТВИЕ 2. Пусть G – esn-группа и G’ – esn’-группа.
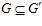 <=>
<=> 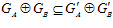 .
.
Доказательство. Так как 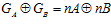 и
и 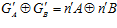 , то нетрудно видеть, что
, то нетрудно видеть, что 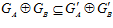 <=>
<=> 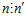 <=>
<=>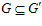 .
.
СЛЕДСТВИЕ 3. Пусть G – esn-группа и 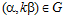 , причем
, причем 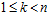 . Тогда такое число k единственно.
. Тогда такое число k единственно.
Доказательство непосредственно следует из теоремы II.
ОПРЕДЕЛЕНИЕ. Пару целых положительных чисел (k, n) таких, что: 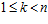 , будем называть инвариантом es-группы G, если
, будем называть инвариантом es-группы G, если 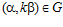 .
.
СЛЕДСТВИЕ 4. Пусть G, G1, G2 –es-группы с инвариантами (n, k), 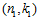 ,
, 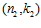 , соответственно.
, соответственно.
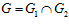 <=> одновременно выполнены условия: 1)
<=> одновременно выполнены условия: 1) 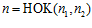 ; 2)
; 2) 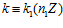 ; 3)
; 3) 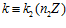 .
.
Доказательство, очевидно, следует из теоремы II.
СЛЕДСТВИЕ 5. Пусть G, G1, G2 – es-группы с инвариантами (n, k), 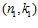 ,
, 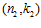 , соответственно. Группа G является наименьшей es-группой, содержащей группы G1 и G2 в качестве подгрупп тогда и только тогда, когда одновременно выполнены условия: 1)
, соответственно. Группа G является наименьшей es-группой, содержащей группы G1 и G2 в качестве подгрупп тогда и только тогда, когда одновременно выполнены условия: 1) 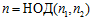 ; 2)
; 2) 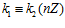 .
.
Доказательство, очевидно, следует из теоремы II.
Замечание. Нетрудно видеть, что для данных es-групп G1 и G2 es-группа G, содержащая группы G1 и G2 в качестве подгрупп, всегда существует. В крайнем случае, число п = 1. В этом случае, 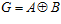 . Следовательно, множество es-групп для различных п образует верхнюю полурешетку по включению.
. Следовательно, множество es-групп для различных п образует верхнюю полурешетку по включению.
СЛЕДСТВИЕ 6. Пусть G = {Gi } – семейство различных es-групп, где для каждого номера i инвариантом группы Gi является пара целых чисел (ni, ki ). Если для различных номеров i и j числа ki и kj равны, а числа ni и nj не равны, то множество G образует решетку по включению.
Доказательство. Пусть для различных номеров i и j числа ki и kj равны, а числа ni и nj не равны. В этом случае, по теореме II, группа Gi содержится в группе Gj тогда и только тогда, когда число nj делится на число ni. Отсюда, очевидно, следует, что множество G образует решетку по включению.
ТЕОРЕМА III. Если семейство различных es-групп G = {Gi}, где для каждого номера i инвариантом группы Gi является пара целых чисел (ni, ki ), образует решетку по включению, то числа ni и nj различны для различных номеров i и j.
Доказательство. Необходимость. Пусть семейство es-групп G = {Gi}, где для каждого номера i инвариантом группы Gi является пара целых чисел (ni, ki ), образует решетку по включению, и пусть для различных номеров i и j числа ni и nj равны и равны п. Тогда, по следствию 4 теоремы II, пересечение групп Gi и Gj существует тогда и только тогда, когда числа ki и kj сравнимы по модулю п в кольце целых чисел Z. А поскольку, для чисел ki и kj выполняются условия: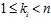 ,
,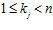 ,то отсюда вытекает, что ki = kj .Следовательно, группы Gi и Gj совпадают, что противоречит условию. Таким образом, доказано, что
,то отсюда вытекает, что ki = kj .Следовательно, группы Gi и Gj совпадают, что противоречит условию. Таким образом, доказано, что 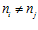 для различных номеров i и j.
для различных номеров i и j.
ОПРЕДЕЛЕНИЕ. es-группу G* будем называть минимальной, если она не содержит в качестве собственной подгруппы никакую другую es-группу. es-группу G* будем называть максимальной, если не существует es-группы, отличной от прямой суммы 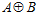 , содержащей группу G* в качестве собственной подгруппы.
, содержащей группу G* в качестве собственной подгруппы.
ТЕОРЕМА IV. Пусть G – es-группа. Группа G является минимальной es-группой <=> ранг группы G равен 1.
Доказательство. Пусть группа G является минимальной es-группой и предположим, что ее ранг равен двум. Тогда, по следствию 2 теоремы II, группа G содержит собственную подгруппу, являющуюся es-группой, что противоречит минимальности группы G. Следовательно, ранг группы G равен единице.
Обратно. Нетрудно видеть, что es-группами ранга 1 являются группы 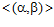 и
и 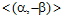 . Поскольку, ни одна из этих групп не является подгруппой другой, а подгруппой циклической группы является группа циклическая, то, очевидно, es-группа ранга 1 является минимальной.
. Поскольку, ни одна из этих групп не является подгруппой другой, а подгруппой циклической группы является группа циклическая, то, очевидно, es-группа ранга 1 является минимальной.
ТЕОРЕМА V. Пусть G – esn-группа. Группа G является максимальной es-группой тогда и только тогда, когда п – простое число.
Доказательство. Пусть группа G является максимальной es-группой, тогда ее ранг равен двум, поскольку, es-группа ранга 1, всегда содержится в качестве собственной подгруппы в es-группе ранга 2. Следовательно, es-группа G есть esn-группа для некоторого целого положительного числа п, отличного от единицы.
Предположим, что число п не является простым, то есть является составным. Тогда существует целое положительное число п’, отличное от единицы, являющееся собственным делителем числа п. Следовательно, по теореме II, существует es-группа G’, содержащая группу G в качестве собственной подгруппы, что противоречит максимальности группы G. Следовательно, число п не может быть составным, то есть оно является простым.
Обратно. Пусть es-группа G есть esn-группа, где п – целое положительное число, отличное от единицы, и являющееся простым. Тогда, по теореме II, поскольку, число п не имеет нетривиальных собственных делителей, следует, что не существует es-группы, содержащей группу G в качестве собственной подгруппы. Таким образом, группа G является максимальной es-группой .
ЛЕММА 1. Пусть G – esn-группа. Пары 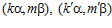 одновременно являются элементами группы G, где k, k’, m, m’ – целые числа, не делящиеся на число п, если существует целое число r такое, что в кольце целых чисел выполняются сравнения:
одновременно являются элементами группы G, где k, k’, m, m’ – целые числа, не делящиеся на число п, если существует целое число r такое, что в кольце целых чисел выполняются сравнения: 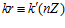 ,
, 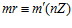 .
.
Доказательство. Пусть k, k’, m, m’ – целые числа, не делящиеся на число п, и пусть существует целое число r такое, что в кольце целых чисел Z выполняются сравнения: 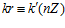 и
и 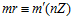 . Тогда для некоторых целых чисел u и v имеют место равенства: k’ =kr +un, m’ =mr +vn. Следовательно,
. Тогда для некоторых целых чисел u и v имеют место равенства: k’ =kr +un, m’ =mr +vn. Следовательно,
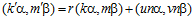 .
.
Поскольку,  , а группа
, а группа 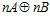 является подгруппой каждой esn-группы, то, значит, пара
является подгруппой каждой esn-группы, то, значит, пара 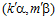 есть элемент той же esn-группы, что и пара
есть элемент той же esn-группы, что и пара 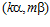 .
.
ЛЕММА 2. Пусть G – esn-группа где п – целое положительное число, отличное от единицы, и пусть для некоторых целых чисел k, k’, m, m’, не делящихся на число п, пары 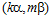 и
и 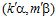 принадлежат группе G. Тогда для любого целого числа r в кольце целых чисел Z одновременно выполняются или не выполняются сравнения:
принадлежат группе G. Тогда для любого целого числа r в кольце целых чисел Z одновременно выполняются или не выполняются сравнения: 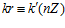 и
и 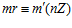 .
.
Доказательство. Предположим, что для некоторого целого числа r в кольце целых чисел Z числа kr и k’ сравнимы по модулю п, а числа mr и m’ по модулю п не сравнимы. Поскольку, пара 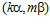 является элементом группы G, то и пара
является элементом группы G, то и пара 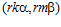 принадлежит группе G , а так как пара
принадлежит группе G , а так как пара 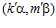 также является элементом группы G , то, по теореме В, числа mr и m’ должны быть сравнимы по модулю п в кольце целых чисел Z, что противоречит нашему предположению. Следовательно, данное предположение не верно, а, значит, доказываемое условие леммы выполняется.
также является элементом группы G , то, по теореме В, числа mr и m’ должны быть сравнимы по модулю п в кольце целых чисел Z, что противоречит нашему предположению. Следовательно, данное предположение не верно, а, значит, доказываемое условие леммы выполняется.
ЛЕММА 3. Пусть G – esn-группа, где п – целое положительное число, отличное от единицы, и пусть пара (а, b) является элементом группы G для некоторых элементов а группы А и b группы В, причем пара (а, b) не принадлежит группе 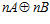 . Если подгруппа Н группы
. Если подгруппа Н группы 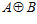 содержит прямую сумму
содержит прямую сумму 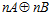 в качестве собственной подгруппы и пару (а, b) в качестве своего элемента и число п является простым, то группа G является подгруппой группы Н.
в качестве собственной подгруппы и пару (а, b) в качестве своего элемента и число п является простым, то группа G является подгруппой группы Н.
Доказательство. Пусть пара (a’, b’) принадлежит группе G для некоторых элементов a’ группы А, не принадлежащего подгруппе пА, и b группы В, не принадлежащего подгруппе пВ. Покажем, что пара (a’, b’) также является элементом группы Н. Пусть
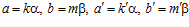 ,
,
где k, k’, m, m’ – целые числа, не делящиеся на число п. Поскольку число п является простым, то, как известно из теории сравнений в кольце целых чисел Z, существует целое число r такое, что в кольце Z выполняются сравнение:
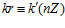 ,
,
а тогда, по лемме 2, для числа r в кольце Z выполняются сравнение:
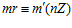 .
.
Тогда для некоторых целых чисел u и v имеют место равенства: k’ = kr + un, m’ = mr + vn .
Следовательно,
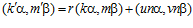
Поскольку, пара  , а группа
, а группа 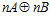 является подгруппой группы Н, то пара
является подгруппой группы Н, то пара 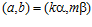 является элементом группы Н, а, значит, и пара
является элементом группы Н, а, значит, и пара 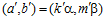 также является элементом группы Н.
также является элементом группы Н.
ТЕОРЕМА VI. Максимальная es-группа является максимальной подгруппой группы 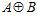 .
.
Доказательство. Пусть G – esn-группа, где п – целое положительное число, отличное от единицы, является максимальной es-группой, и пусть Н – подгруппа группы 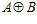 , содержащая группу G в качестве собственной подгруппы. Тогда группа Н содержит прямую сумму
, содержащая группу G в качестве собственной подгруппы. Тогда группа Н содержит прямую сумму 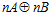 в качестве подгруппы.
в качестве подгруппы.
С другой стороны, найдутся элементы а группы А, не принадлежащий подгруппе пА, и b группы В, не принадлежащий подгруппе пВ, такие, что пара (а, b) принадлежит группе Н и не принадлежит группе G. Следовательно, существуют целые числа k и m такие, что 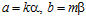 . А, поскольку, число п является простым, то наибольший общий делитель чисел k и n равен наибольшему общему делителю чисел k и m и равен единице, тогда, как доказано ранее ([2], [3], [8]), существует единственная подпрямая сумма G’ групп А и В, содержащая пару (а, b) в качестве своего элемента. Следовательно, по лемме 3, группа G’ является подгруппой группы Н. Таким образом, сумма групп G + G’ также является подгруппой группы Н.
. А, поскольку, число п является простым, то наибольший общий делитель чисел k и n равен наибольшему общему делителю чисел k и m и равен единице, тогда, как доказано ранее ([2], [3], [8]), существует единственная подпрямая сумма G’ групп А и В, содержащая пару (а, b) в качестве своего элемента. Следовательно, по лемме 3, группа G’ является подгруппой группы Н. Таким образом, сумма групп G + G’ также является подгруппой группы Н.
С другой стороны, так как число п – простое, то, как доказано ранее ([2], [3], [8]), выполняется равенство:
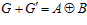 .
.
Значит, группа Н совпадает с прямой суммой 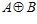 , и, следовательно, максимальная подпрямая сумма G групп А и В одновременно является максимальной подгруппой группы
, и, следовательно, максимальная подпрямая сумма G групп А и В одновременно является максимальной подгруппой группы 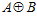 .
.
ТЕОРЕМА VII. Пусть G – esn-группа, где п – целое положительное число, отличное от единицы. Если число п является простым, то индекс подгруппы G в группе 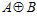 равен п.
равен п.
Доказательство. Пусть число п является простым, тогда, по теореме V, группа G является максимальной подгруппой группы 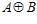 , а, как известно, индекс максимальной подгруппы есть число простое. С другой стороны, в этом случае, индекс подгруппы
, а, как известно, индекс максимальной подгруппы есть число простое. С другой стороны, в этом случае, индекс подгруппы 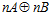 в группе
в группе 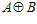 , очевидно, равен п. А, поскольку, прямая сумма
, очевидно, равен п. А, поскольку, прямая сумма 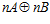 является подгруппой группы G, то индекс подгруппы G группы
является подгруппой группы G, то индекс подгруппы G группы 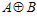 является делителем числа п, а, значит, равен п. Что и требовалось доказать.
является делителем числа п, а, значит, равен п. Что и требовалось доказать.
Библиографический список
-
Куликов Л. Я. О подпрямых суммах абелевых групп без кручения первого ранга // ХII Всес. алгебр. коллоквиум. – Свердловск. 1973. – С. 30.
-
Трухманов В. Б. О некоторых специальных и р-специальных группах // Исследования в области естественных наук. – Июнь 2014. – № 6 [Электронный ресурс]. URL: http://science.snauka.ru/2014/06/7405 (дата обращения: 25.06.2014).
-
Трухманов В. Б. Подпрямые суммы абелевых групп без кручения ранга 1. // Фундаментальная и прикладная математика. 2007. Т.13. №3. – С. 209-221.
-
Фукс Л. Бесконечные абелевы группы, т.1. – М. Мир, 1974.
-
Широков Л. В. О
 -бикомпактах. // Известия РАН. 1992. т. 56. № 6. – С. 1316-1327.
-бикомпактах. // Известия РАН. 1992. т. 56. № 6. – С. 1316-1327. -
Широков Л. В. О продолжении непрерывных отображений и аппроксимативной связности // Проблемы современной науки, Центр научного знания «ЛОГОС». 2013. Выпуск 9. – С. 3-9.
-
Широков Л. В. Теория аналитических функций. Аспекты приложений / Л.В. Широков, Н.П. Ямпурин, В.Д. Садков. – Арзамас: АГПИ, 2004. – 188 с.
-
Trukhmanov V. B. On subdirect sums of abelian torsion-free groups of rank 1. // Journal of Mathematical Sciences. 2008. Vol.154. №3. – P. 422-429.