В данной статье рассматриваются свойства так называемых специальных и р-специальных групп, введенных и изучаемых автором в работах [1] и [4]. Необходимые определения и обозначения приведены в работах [1] – [8].
ОПРЕДЕЛЕНИЕ 1. Пусть А и B – рациональные группы. Упорядоченную пару элементов (α, β), где 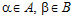 , будем называть базисом подпрямой суммы G групп А и В, если GА = <α>, GВ = <β>.
, будем называть базисом подпрямой суммы G групп А и В, если GА = <α>, GВ = <β>.
ОПРЕДЕЛЕНИЕ 2. Пусть р – простое число. Абелеву группу без кручения G ранга 2, будем называть р-специальной, если
1) группа G является подпрямой суммой рациональных групп, изоморфных рациональной группе Q р;
2) группа G обладает базисом.
Пусть далее, для некоторых делимых рациональных групп А и B, G – специальная группа с базисом (α, β) – подгруппа прямой суммы групп А и В, Z – кольцо целых чисел. Для любого простого числа р, через G р будем обозначать множество пар вида 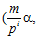
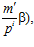 где i = 0, 1, 2, … ; т, m′ – целые числа, взаимно простые с числом р.
где i = 0, 1, 2, … ; т, m′ – целые числа, взаимно простые с числом р.
ЛЕММА 1. Множество G р образует подгруппу группы G.
Доказательство. Данное утверждение следует из очевидной замкнутости множества G р относительно операции сложения.
ОПРЕДЕЛЕНИЕ. Пусть A′ и B′ – рациональные группы, изоморфные группе Q р, для некоторого простого числа р, подгруппу прямой суммы групп A′ и B′ будем называть р-специальной, если она является подпрямой суммой групп A′ и B′, индуцированной группой Q р/Z, с базисом (α, β).
Введем следующее обозначение: если А и B – делимые рациональные группы и G – специальная группа с базисом (α, β), где 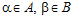 , то для любого натурального числа n ≠ 1 через Gn будем обозначать подмножество группы G, состоящее из всех пар вида
, то для любого натурального числа n ≠ 1 через Gn будем обозначать подмножество группы G, состоящее из всех пар вида 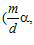
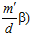 , где т, m′ – целые числа, взаимно простые с числом d, для каждого натурального делителя d числа п.
, где т, m′ – целые числа, взаимно простые с числом d, для каждого натурального делителя d числа п.
ЛЕММА 2. 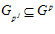 , для любого натурального числа j.
, для любого натурального числа j.
Доказательство непосредственно следует из определения G р.
ПРЕДЛОЖЕНИЕ 1. Для любого простого числа р, выполняются условия:
1) подгруппа G р группы G является р-специальной подгруппой;
2) группа G р может быть получена как объединение бесконечной возрастающей цепи своих подгрупп 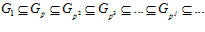 , где
, где 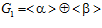 ;
;
3) система 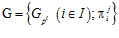 , где
, где 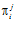 – естественное вложение
– естественное вложение 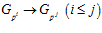 , образует прямой спектр, причем
, образует прямой спектр, причем 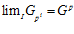 .
.
Доказательство. Пусть р – простое число. Рассмотрим множество G р. По определению, 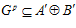 , покажем, что множество G p образует подпрямую сумму групп
, покажем, что множество G p образует подпрямую сумму групп 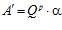 и
и 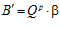 , индуцированную группой Q р/Z, с базисом (α, β), причем группа Gр является подгруппой группы G.
, индуцированную группой Q р/Z, с базисом (α, β), причем группа Gр является подгруппой группы G.
Действительно, рассмотрим два произвольных элемента группы G p: 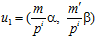 и
и 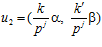 , причем,
, причем, 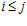 . Поскольку рi является делителем р j, то, по определению группы
. Поскольку рi является делителем р j, то, по определению группы 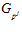 , элементы и1 и и2, а также их сумма, принадлежат
, элементы и1 и и2, а также их сумма, принадлежат 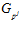 , и, следовательно, множеству G р.
, и, следовательно, множеству G р.
Таким образом, G р – группа.
Далее, пусть элемент 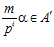 , тогда числа т и рi взаимно просты, и, следовательно, существует число m′ , взаимно простое с числом рi такое, что элемент
, тогда числа т и рi взаимно просты, и, следовательно, существует число m′ , взаимно простое с числом рi такое, что элемент 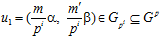 , причем ни для какого числа m″ , несравнимого с числом m′ по модулю рi в кольце Z, элемент
, причем ни для какого числа m″ , несравнимого с числом m′ по модулю рi в кольце Z, элемент 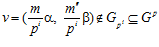 .
.
Таким образом, проекция 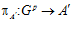 является эпиморфизмом. Аналогично получаем, что проекция
является эпиморфизмом. Аналогично получаем, что проекция 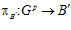 также является эпиморфизмом. Следовательно, группа Gр есть подпрямая сумма групп A′ и B′, индуцированная группой Q р/Z.
также является эпиморфизмом. Следовательно, группа Gр есть подпрямая сумма групп A′ и B′, индуцированная группой Q р/Z.
Условие 2) непосредственно следует из определения группы G р, а также из определения групп 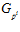 для каждого целого положительного числа i. Условие 3) предложения непосредственно следует из определения прямого спектра.
для каждого целого положительного числа i. Условие 3) предложения непосредственно следует из определения прямого спектра.
ПРЕДЛОЖЕНИЕ 2. Для любого элемента v группы G, не принадлежащего группе 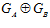 , существуют и причем единственные, с точностью до нумерации, простые числа р1, р2, …, рr такие, что v = v0+ v1 + v2 + … + vr, где
, существуют и причем единственные, с точностью до нумерации, простые числа р1, р2, …, рr такие, что v = v0+ v1 + v2 + … + vr, где 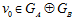 ,
,
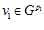 ,
, 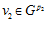 , …,
, …, 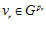 .
.
Доказательство. Пусть п – целое положительное число, отличное от единицы, такое, что 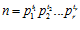 , где числа р1, р2, …, рr – различные простые, и пусть элемент
, где числа р1, р2, …, рr – различные простые, и пусть элемент 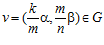 , где числа k и т – целые, взаимно простые с числом п. Тогда, очевидно, пара
, где числа k и т – целые, взаимно простые с числом п. Тогда, очевидно, пара 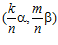 может быть представлена в виде:
может быть представлена в виде:
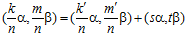 ,
,
где s и t – целые числа, а k’ и m’ - наименьшие целые положительные числа такие. что k′ сравнимо с k, а m′ сравнимо с т по модулю nZ в кольце Z. Пары 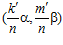 и (sα, tβ) принадлежат группе G, причем, как легко видеть, пара
и (sα, tβ) принадлежат группе G, причем, как легко видеть, пара 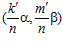 может быть представлена в виде:
может быть представлена в виде:
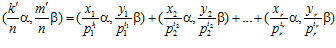 ,
,
где 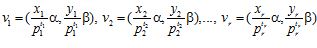 . Что и требовалось доказать.
. Что и требовалось доказать.
ЛЕММА. Для любого целого положительного числа k и любых целых взаимно простых чисел р1, р2, …, рk выполняется условие: если сумма
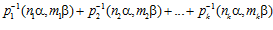 ,
,
где п1, п2, …, пk, m1, m2, …, mk – целые числа, причем, для каждого номера i = 1, 2, …, k выполняются условия: 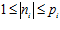 ,
,
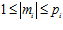 , принадлежит группе G, то и каждый из элементов
, принадлежит группе G, то и каждый из элементов 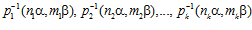 принадлежит группе G.
принадлежит группе G.
Доказательство проведем методом математической индукции по числу k. Пусть k = 2, то есть сумма пар
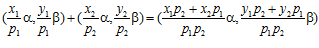
принадлежит группе G. Следовательно, если одна из пар 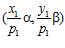 или
или 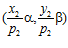 принадлежит группе G, то, очевидно, и другая пара также принадлежит группе G. Поэтому, предположим, что никакая из пар
принадлежит группе G, то, очевидно, и другая пара также принадлежит группе G. Поэтому, предположим, что никакая из пар 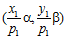 и
и 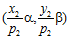 не принадлежит подпрямой сумме G групп А и В, индуцированной группой Q/Z. Но тогда, по определению подпрямой суммы групп, существуют целые числа
не принадлежит подпрямой сумме G групп А и В, индуцированной группой Q/Z. Но тогда, по определению подпрямой суммы групп, существуют целые числа 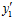 ,
, 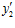 такие, что
такие, что
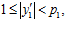
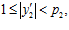
и такие, что пары 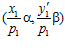 и
и 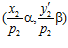 принадлежат группе G. Значит, и сумма
принадлежат группе G. Значит, и сумма
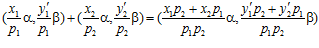
также принадлежит группе G. Тогда, числа у1р2 + у2р1 и 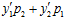 сравнимы по модулю р1р2 в кольце Z, следовательно, в кольце Z имеет место сравнение:
сравнимы по модулю р1р2 в кольце Z, следовательно, в кольце Z имеет место сравнение:
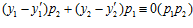 .
.
Но, поскольку, для чисел 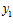 ,
, 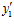 ,
, 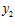 ,
, 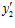 выполняются условия:
выполняются условия:
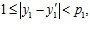
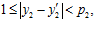
то сумма 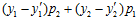 равна либо нулю, либо р1р2. Тогда, в первом случае получаем, что
равна либо нулю, либо р1р2. Тогда, в первом случае получаем, что 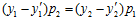 . Следовательно, поскольку, по условию, числа р1 и р2 взаимно просты, то разность
. Следовательно, поскольку, по условию, числа р1 и р2 взаимно просты, то разность 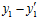 делится на число р1, а разность
делится на число р1, а разность 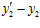 делится на число р2. Во втором случае, как нетрудно видеть, получаются точно такие же выводы.
делится на число р2. Во втором случае, как нетрудно видеть, получаются точно такие же выводы.
Таким образом, в кольце Z имеют место сравнения: 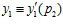 ,
, 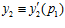 , и, значит, пары
, и, значит, пары 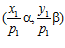 и
и 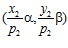 есть элементы группы G.
есть элементы группы G.
Далее предположим, что для любого числа пар – слагаемых, меньшего числа k, лемма выполняется. Тогда, взяв сумму пар
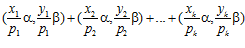 ,
,
и, разбив ее произвольным образом на сумму двух слагаемых, мы, используя предположение индукции и изложенные выше рассуждения, легко сможем показать, что каждая из пар 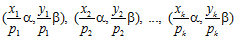 принадлежит G. Следовательно, по принципу индукции, лемма выполняется для любого числа пар – слагаемых.
принадлежит G. Следовательно, по принципу индукции, лемма выполняется для любого числа пар – слагаемых.
ТЕОРЕМА 3. 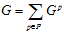 , причем для любых различных простых чисел р и q справедливо равенство:
, причем для любых различных простых чисел р и q справедливо равенство: 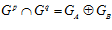 , где группы GA и GB – ядра подпрямой суммы G групп А и В.
, где группы GA и GB – ядра подпрямой суммы G групп А и В.
Доказательство. Легко видеть, что для любого простого числа р группа Gp является подгруппой группы G. Следовательно, 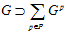 .
.
Обратно. По предложению 2 пара 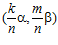 , где числа k и т – целые, взаимно простые с числом п, может быть представлена в виде:
, где числа k и т – целые, взаимно простые с числом п, может быть представлена в виде: 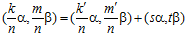 , где s и t – целые числа, а k′ и m′ – наименьшие целые положительные числа такие, что k′ сравнимо с k, а m′ сравнимо с т по модулю nZ в кольце целых чисел Z, а пара
, где s и t – целые числа, а k′ и m′ – наименьшие целые положительные числа такие, что k′ сравнимо с k, а m′ сравнимо с т по модулю nZ в кольце целых чисел Z, а пара 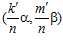 может быть представлена в виде:
может быть представлена в виде:
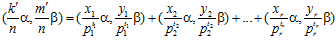 ,
,
где, по лемме, каждое слагаемое принадлежит группе G. Следовательно, 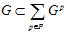 . Таким образом,
. Таким образом, 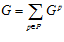 .
.
Второе равенство в условии теоремы очевидно. Теорема доказана.
СЛЕДСТВИЕ. Пусть для каждого простого числа р, через Н р обозначим подпрямую сумму рациональных групп A′ и B′ ,
изоморфных группе Q р и являющихся подгруппами групп А и В, соответственно, индуцированную группой Q р/Z, с одним и тем же базисом (α, β) . Тогда для каждого множества 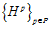 , подпрямая сумма G групп А и B, индуцированная группой Q/Z, с базисом (α, β) такая, что Н р= G p, существует и единственна.
, подпрямая сумма G групп А и B, индуцированная группой Q/Z, с базисом (α, β) такая, что Н р= G p, существует и единственна.
Доказательство. Пусть дано некоторое множество 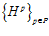 подпрямых сумм рациональных групп A′ и B′ , изоморфных группам Q р, для каждого простого числа р, и являющихся подгруппами групп А и В, соответственно, индуцированных группами Q р/Z, с одним и тем же базисом (α, β). Тогда, применив рассуждения, аналогичные приведенным в теореме, мы получим, что
подпрямых сумм рациональных групп A′ и B′ , изоморфных группам Q р, для каждого простого числа р, и являющихся подгруппами групп А и В, соответственно, индуцированных группами Q р/Z, с одним и тем же базисом (α, β). Тогда, применив рассуждения, аналогичные приведенным в теореме, мы получим, что 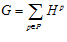 .
.
ОПРЕДЕЛЕНИЕ. Последовательность целых положительных чисел
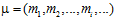
будем называть характеристической последовательностью группы G р для данного базиса (α, β) , если для каждого номера i, число тi является наименьшим положительным, таким, что элемент 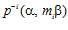 принадлежит р-специальной подгруппе G р группы G, где р – простое число.
принадлежит р-специальной подгруппе G р группы G, где р – простое число.
Поскольку, с точностью до знака, подпрямая сумма двух изоморфных рациональных групп имеет два базиса, то и характеристических последовательностей у такой подпрямой суммы будет две. Условие, описывающее характеристическую последовательность, и условие, связывающее характеристические последовательности одной и той же подпрямой суммы данных групп сформулированы в следующих предложениях.
ПРЕДЛОЖЕНИЕ 4. Последовательность целых положительных чисел 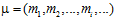 является характеристической для некоторой р-специальной подгруппы G р группы G тогда и только тогда, когда выполняются условия:
является характеристической для некоторой р-специальной подгруппы G р группы G тогда и только тогда, когда выполняются условия:
-
0 < тi < рi, для каждого номера i = 1, 2, …;
-
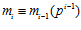 для каждого номера i = 2, 3, ….
для каждого номера i = 2, 3, ….
Доказательство непосредственно следует из определения подпрямой суммы, характеристической последовательности.
СЛЕДСТВИЕ. Характеристическая последовательность группы G р сходится к некоторому целому р-адическому числу ρ – единичному элементу кольца целых р-адических чисел.
Доказательство непосредственно следует из определения целого р-адического числа, а также из условия, что в данной последовательности отсутствуют нули.
Итак, на основании выше доказанных предложений мы можем сформулировать основную теорему.
ТЕОРЕМА 5. Для данного простого числа р существует взаимно-однозначное соответствие между множеством всех р-специальных групп с фиксированным базисом и мультипликативной группой обратимых элементов кольца целых р-адических чисел.
Существует взаимно-однозначное соответствие между множеством всех специальных групп с фиксированным базисом и мультипликативной группой обратимых элементов кольца универсальных чисел – 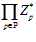 , где
, где 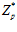 – кольцо целых р-адических чисел.
– кольцо целых р-адических чисел.
Библиографический список
- Trukhmanov V.B. On subdirect sums of abelian torsion-free groups of rank 1. // Journal of Mathematical Sciences. 2008. Т.154. №3. – С. 422-429.
- Куликов Л.Я. О подпрямых суммах абелевых групп без кручения первого ранга // ХII Всес. алгебр. коллоквиум. – Свердловск. 1973. – С. 30.
- Куликов Л.Я. Подпрямые разложения счетных абелевых групп без кручения // Х Всес. алгебр. коллоквиум. – Новосибирск. 1969. – С. 18-19.
- Трухманов В.Б. Подпрямые суммы абелевых групп без кручения ранга 1. // Фундаментальная и прикладная математика. 2007. Т.13. №3. – С. 209-221.
- Фукс Л. Бесконечные абелевы группы, т.1. – М. Мир, 1974.
- Широков Л.В. О -бикомпактах. // Известия РАН. 1992. т. 56. № 6. – С. 1316-1327.
- Широков Л.В. О продолжении непрерывных отображений и аппроксимативной связности // Проблемы современной науки, Центр научного знания «ЛОГОС». 2013. Выпуск 9. – С. 3-9.
- Широков Л.В. Теория аналитических функций. Аспекты приложений / Л.В. Широков, Н.П. Ямпурин, В.Д. Садков. – Арзамас: АГПИ, 2004. – 188 с.
