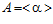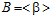Всюду в статье (если не сказано иначе) все группы – абелевы, А и В – бесконечные циклические группы, и , п – целое положительное число, n > 1.

Определение 1. Подгруппа G прямого произведения 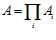 абелевых групп называется подпрямой суммой групп А_i, если для каждого i отображение  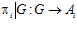является эпиморфизмом, где 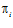– проекция прямого произведения А на прямой сомножитель А_i. [4]

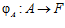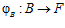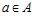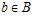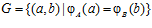Как установлено [4], для того чтобы группа G являлась подпрямой суммой групп А и В необходимо и достаточно, чтобы существовали группа F и такие эпиморфизмы и , что для любых элементов и  ,  . Назовем F порождающей группой для подпрямой суммы G групп А и В, а эпиморфизмы 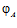и 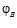назовем определяющими для группы G.

Определение 2. Если для некоторого данного числа 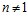, группа G является подпрямой суммой данных групп А и В, порожденной конечной циклической группой Z_п – аддитивной группой кольца вычетов по модулю п – то группу G будем называть элементарной специальной п-группой (esп-группой). В случае, когда число п неизвестно или может быть любым, такую группу мы будем называть es-группой.

В данной статье продолжено изучение свойств esn-групп в зависимости от числа п, а также множества G всех es-групп. Ранее были доказаны ([2], [3], [8]) следующие утверждения, используемые в данной статье:

ТЕОРЕМА А. Для любого целого положительного числа 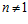, существует взаимно-однозначное соответствие f между множеством элементарных специальных групп, индуцированных группой Z_п,
и мультипликативной группой обратимых элементов кольца вычетов по модулю п.

ТЕОРЕМА Б. Пусть G – esn-группа, . Тогда,  <=>  .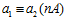

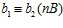ТЕОРЕМА В. Пусть и 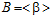, , 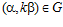где G  – esn-группа, k – взаимно простое с п целое число,  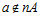и 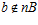. Тогда, 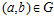<=> существуют целые числа t и s такие, что 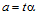, , 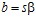и 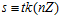, и такие , что п не является их делителем.

В данной статье доказывается следующее основное утверждение для класса esп-групп:

— esn-группа G, является подгруппой esn’-группы G’ <=> 1) 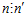; 2) .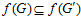

— группа G максимальна во множестве G <=> G  – esp-группа для простого числа p. Минимальной es-группы во множестве G не существует.

Необходимые определения и обозначения приведены в работах [1] – [8].

ТЕОРЕМА I. Пусть G – esn-группа с парой определяющих эпиморфизмов 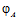,  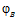и G’ – esn’-группа с парой определяющих эпиморфизмов , . 

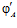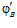Тогда 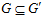<=> для любых элементов а группы А, не принадлежащего подгруппе пА, и b группы В, не принадлежащего подгруппе пВ, выполняется условие:

.

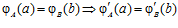Доказательство непосредственно следует из определения esn-группы.

ТЕОРЕМА II. Пусть G – esn-группа и G’ – esn’-группа, 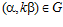, , 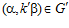где k – целое число, принадлежащее интервалу от 1 до n, k’ – целое число, принадлежащее интервалу от 1 до n’.

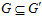 <=> 1) 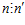; 2) .

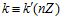Доказательство. Пусть 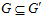, тогда одновременно 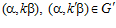. Следовательно, по теореме Б, 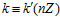. С другой стороны, по теореме В, для любых целых чисел t и s, не делящихся на п, имеет место следующее условие:

=>

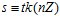для чисел t и s взаимно простых с числом п’. Следовательно, очевидно, .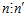

Обратно. Пусть 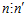, , 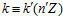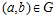. Тогда, если 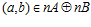, то, очевидно, 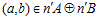. Если же 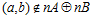, то, по теореме В, существуют целые числа t и s, взаимно простые с числом п, такие, что 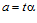,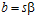и 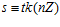. Тогда 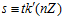и, следовательно, 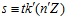. Отсюда, по теореме В, следует, что  .

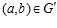СЛЕДСТВИЕ 1. Пусть G – esn-группа. Тогда существует esn-группа – подгруппа группы G.

Доказательство, очевидно, непосредственно следует из теоремы II.

СЛЕДСТВИЕ 2. Пусть G – esn-группа и G’ – esn’-группа.

<=>  .

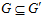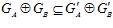Доказательство. Так как 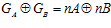и 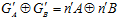, то нетрудно видеть, что <=> <=>.

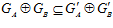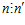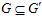СЛЕДСТВИЕ 3. Пусть G – esn-группа и 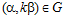, причем 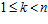. Тогда такое число k единственно.

Доказательство непосредственно следует из теоремы II.

ОПРЕДЕЛЕНИЕ. Пару целых положительных чисел (k, n) таких, что: 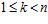, будем называть инвариантом es-группы G, если .

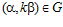СЛЕДСТВИЕ 4. Пусть G, G₁, G₂ –es-группы с инвариантами (n, k), 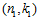, , 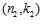соответственно.

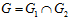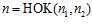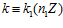<=> одновременно выполнены условия: 1) ; 2) ; 3) .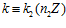

Доказательство, очевидно, следует из теоремы II.

СЛЕДСТВИЕ 5. Пусть G, G₁, G₂ – es-группы с инвариантами (n, k), 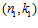, , 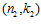соответственно. Группа G является наименьшей es-группой, содержащей группы G₁ и G₂ в качестве подгрупп тогда и только тогда, когда одновременно выполнены условия: 1) 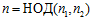; 2) .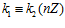

Доказательство, очевидно, следует из теоремы II.

Замечание. Нетрудно видеть, что для данных es-групп G₁ и G₂ es-группа G, содержащая группы G₁ и G₂ в качестве подгрупп, всегда существует. В крайнем случае, число п = 1. В этом случае, 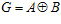. Следовательно, множество es-групп для различных п образует верхнюю полурешетку по включению.

СЛЕДСТВИЕ 6. Пусть G = {G_i } – семейство различных es-групп, где для каждого номера i инвариантом группы G_i является пара целых чисел (n_i, k_i ). Если для различных номеров i и j числа k_i и k_j равны, а числа n_i и n_j не равны, то множество G образует решетку по включению.

Доказательство. Пусть для различных номеров i и j числа k_i и k_j равны, а числа n_i и n_j не равны. В этом случае, по теореме II, группа G_i содержится в группе G_j тогда и только тогда, когда число n_j делится на число n_i. Отсюда, очевидно, следует, что множество G образует решетку по включению.

ТЕОРЕМА III. Если семейство различных es-групп G = {G_i}, где для каждого номера i инвариантом группы G_i является пара целых чисел (n_i, k_i ), образует решетку по включению, то числа n_i и n_j различны для различных номеров i и j.

Доказательство. Необходимость. Пусть семейство es-групп G = {G_i}, где для каждого номера i инвариантом группы G_i является пара целых чисел (n_i, k_i ), образует решетку по включению, и пусть для различных номеров i и j числа n_i и n_j равны и равны п. Тогда, по следствию 4 теоремы II, пересечение групп G_i и G_j существует тогда и только тогда, когда числа k_i и k_j сравнимы по модулю п в кольце целых чисел Z. А поскольку, для чисел k_i и k_j выполняются условия: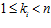,,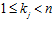то отсюда вытекает, что k_i = k_j .Следовательно, группы G_i и G_j совпадают, что противоречит условию. Таким образом, доказано, что 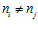для различных номеров i и j.

ОПРЕДЕЛЕНИЕ. es-группу G_* будем называть минимальной, если она не содержит в качестве собственной подгруппы никакую другую es-группу. es-группу G^* будем называть максимальной, если не существует es-группы, отличной от прямой суммы 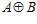, содержащей группу G^* в качестве собственной подгруппы.

ТЕОРЕМА IV. Пусть G – es-группа. Группа G является минимальной es-группой <=> ранг группы G равен 1.

Доказательство. Пусть группа G является минимальной es-группой и предположим, что ее ранг равен двум. Тогда, по следствию 2 теоремы II, группа G содержит собственную подгруппу, являющуюся es-группой, что противоречит минимальности группы G. Следовательно, ранг группы G равен единице.

Обратно. Нетрудно видеть, что es-группами ранга 1 являются группы 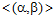и 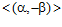. Поскольку, ни одна из этих групп не является подгруппой другой, а подгруппой циклической группы является группа циклическая, то, очевидно, es-группа ранга 1 является минимальной.

ТЕОРЕМА V. Пусть G  – esn-группа. Группа G является максимальной es-группой тогда и только тогда, когда п – простое число.

Доказательство. Пусть группа G является максимальной es-группой, тогда ее ранг равен двум, поскольку, es-группа ранга 1, всегда содержится в качестве собственной подгруппы в es-группе ранга 2. Следовательно, es-группа G есть esn-группа для некоторого целого положительного числа п, отличного от единицы.

Предположим, что число п не является простым, то есть является составным. Тогда существует целое положительное число п’, отличное от единицы, являющееся собственным делителем числа п. Следовательно, по теореме II, существует es-группа G’, содержащая группу G в качестве собственной подгруппы, что противоречит максимальности группы G. Следовательно, число п не может быть составным, то есть оно является простым.

Обратно. Пусть es-группа G есть esn-группа, где п – целое положительное число, отличное от единицы, и являющееся простым. Тогда, по теореме II, поскольку, число п не имеет нетривиальных собственных делителей, следует, что не существует es-группы, содержащей группу G в качестве собственной подгруппы. Таким образом, группа G является максимальной es-группой .

ЛЕММА 1. Пусть G  – esn-группа. Пары 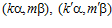одновременно являются элементами группы G, где k, k’, m, m’ – целые числа, не делящиеся на число п, если существует целое число r такое, что в кольце целых чисел выполняются сравнения: , .

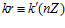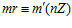Доказательство. Пусть k, k’, m, m’ – целые числа, не делящиеся на число п, и пусть существует целое число r такое, что в кольце целых чисел Z выполняются сравнения: 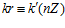 и 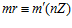. Тогда для некоторых целых чисел u и v имеют место равенства: k’  =kr +un, m’ =mr +vn. Следовательно,

.

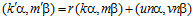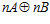Поскольку, , а группа является подгруппой каждой esn-группы, то, значит, пара 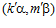есть элемент той же esn-группы, что и пара .

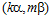ЛЕММА 2. Пусть G – esn-группа где п – целое положительное число, отличное от единицы, и пусть для некоторых целых чисел k, k’, m, m’, не делящихся на число п, пары 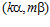и 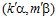 принадлежат группе G. Тогда для любого целого числа r в кольце целых чисел Z одновременно выполняются или не выполняются сравнения: 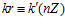и .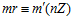

Доказательство. Предположим, что для некоторого целого числа r в кольце целых чисел Z числа kr и k’ сравнимы по модулю п, а числа mr и m’ по модулю п не сравнимы. Поскольку, пара 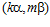является элементом группы G, то и пара 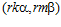принадлежит группе G , а так как пара  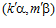также является элементом группы G , то, по теореме В, числа mr и m’ должны быть сравнимы по модулю п в кольце целых чисел Z, что противоречит нашему предположению. Следовательно, данное предположение не верно, а, значит, доказываемое условие леммы выполняется.

ЛЕММА 3. Пусть G – esn-группа, где п – целое положительное число, отличное от единицы, и пусть пара (а, b) является элементом группы G для некоторых элементов а группы А и b группы В, причем пара (а, b) не принадлежит группе 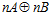. Если подгруппа Н группы  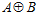содержит прямую сумму  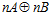в качестве собственной подгруппы и пару (а, b) в качестве своего элемента и число п является простым, то группа G является подгруппой группы Н.

Доказательство. Пусть пара (a’, b’) принадлежит группе G для некоторых элементов a’ группы А, не принадлежащего подгруппе пА, и b группы В, не принадлежащего подгруппе пВ. Покажем, что пара (a’, b’) также является элементом группы Н. Пусть

,

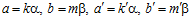где k, k’, m, m’ – целые числа, не делящиеся на число п. Поскольку число п является простым, то, как известно из теории сравнений в кольце целых чисел Z, существует целое число r такое, что в кольце Z выполняются сравнение:

,

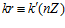а тогда, по лемме 2, для числа r в кольце Z выполняются сравнение:

.

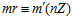Тогда для некоторых целых чисел u и v имеют место равенства: k’ = kr + un, m’ = mr + vn .

Следовательно,

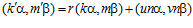
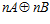Поскольку, пара , а группа  является подгруппой группы Н, то пара 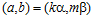является элементом группы Н, а, значит, и пара 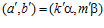также является элементом группы Н.

ТЕОРЕМА VI. Максимальная es-группа является максимальной подгруппой группы .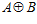

Доказательство. Пусть G – esn-группа, где п – целое положительное число, отличное от единицы, является максимальной es-группой, и пусть Н – подгруппа группы 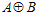, содержащая группу G в качестве собственной подгруппы. Тогда группа Н содержит прямую сумму 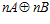в качестве подгруппы.

С другой стороны, найдутся элементы а группы А, не принадлежащий подгруппе пА, и b группы В, не принадлежащий подгруппе пВ, такие, что пара (а, b) принадлежит группе Н и не принадлежит группе G. Следовательно, существуют целые числа k и m такие, что 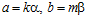. А, поскольку, число п является простым, то наибольший общий делитель чисел k и n равен наибольшему общему делителю чисел k и m и равен единице, тогда, как доказано ранее ([2], [3], [8]), существует единственная подпрямая сумма G’ групп А и В, содержащая пару (а, b) в качестве своего элемента. Следовательно, по лемме 3, группа G’ является подгруппой группы Н. Таким образом, сумма групп G + G’ также является подгруппой группы Н.

С другой стороны, так как число п – простое, то, как доказано ранее ([2], [3], [8]), выполняется равенство:

.

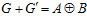Значит, группа Н совпадает с прямой суммой 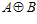, и, следовательно, максимальная подпрямая сумма G групп А и В одновременно является максимальной подгруппой группы .

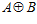ТЕОРЕМА VII. Пусть G – esn-группа, где п – целое положительное число, отличное от единицы. Если число п является простым, то индекс подгруппы G в группе 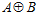 равен п.

Доказательство. Пусть число п является простым, тогда, по теореме V, группа G является максимальной подгруппой группы 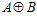, а, как известно, индекс максимальной подгруппы есть число простое. С другой стороны, в этом случае, индекс подгруппы 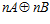в группе 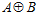, очевидно, равен п. А, поскольку, прямая сумма 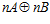является подгруппой группы G, то индекс подгруппы G группы 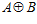является делителем числа п, а, значит, равен п. Что и требовалось доказать.

1. Куликов Л. Я. О подпрямых суммах абелевых групп без кручения первого ранга // ХII Всес. алгебр. коллоквиум. – Свердловск. 1973. – С. 30.
2. Трухманов В. Б. О некоторых специальных и р-специальных группах // Исследования в области естественных наук. – Июнь 2014. – № 6 [Электронный ресурс]. URL: http://science.snauka.ru/2014/06/7405 (дата обращения: 25.06.2014).
   
3. Трухманов В. Б. Подпрямые суммы абелевых групп без кручения ранга 1. // Фундаментальная и прикладная математика. 2007. Т.13. №3. – С. 209-221.
   
4. Фукс Л. Бесконечные абелевы группы, т.1. – М. Мир, 1974.
5. Широков Л. В. О -бикомпактах. // Известия РАН. 1992. т. 56. № 6. – С. 1316-1327.
6. Широков Л. В. О продолжении непрерывных отображений и аппроксимативной связности // Проблемы современной науки, Центр научного знания «ЛОГОС». 2013. Выпуск 9. – С. 3-9.
7. Широков Л. В. Теория аналитических функций. Аспекты приложений / Л.В. Широков, Н.П. Ямпурин, В.Д. Садков. – Арзамас: АГПИ, 2004. – 188 с.
8. Trukhmanov V. B. On subdirect sums of abelian torsion-free groups of rank 1. // Journal of Mathematical Sciences. 2008. Vol.154. №3. – P. 422-429.

Все статьи автора «Трухманов Вячеслав Борисович»