При исследовании процесса старения свинцовых аккумуляторов, хранящихся с залитым электролитом, была установлена величина снижения плотности электролита Dr_К
£ 0,02 г/см³ [1], при которой аккумуляторы следует оправлять на заряд, что позволит им отдавать после 5 лет хранения фактическую ёмкость С_Ф, А·ч, равную или большую 50 % от номинальной ёмкости С_Н, А·ч:

С_Ф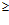0,5С_Н.

Соотнесем полученное при исследовании значение Dr_К с оптимальным значением Dr_КО, г/см³, при котором общие затраты на поддержание готовности аккумуляторов будут минимальными. С этой целью для определения критической плотности электролита по критерию минимальных затрат на поддержание заданной степени заряженности по Dr_КО, рассмотрим приведенную ниже модель. При этом считаем, что общие затраты, необходимые на восстановление номинальной плотности электролита аккумулятора (то есть максимального значения фактической емкости) должны быть минимальными.

Пусть в момент времени t = t₀ плотность электролита равна номинальной r_Н, г/см³. Затем, при хранении аккумулятора его плотность убывает по закону r (t). При достижении плотностью критического значения r_К, г/см³, осуществляется заряд аккумулятора, в результате которого плотность электролита достигает значения r_Н. Считаем, что описанный процесс изменения плотности – периодический с периодом Т. Причём время заряда t_З существенно меньше периода Т, то есть Т » t_З. Вследствие чего процесс заряда можно считать мгновенным. Изменения плотности по времени можно представить в соответствии с рисунком 1 (закономерности изменения плотности r (t) не известны) или записать в виде:

r_Н, если t = t₀+n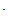T при (n=0, 1, 2, 3…);

r (t-(to+n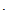T)), если to+n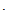T< t <(n+1)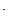T+to,

где t – время хранения аккумулятора, сутки;

T – время снижения величины r_Н до r_К, сутки;

t₀ – время постановки аккумулятора на хранение, сутки;

n – количество периодов Т за время хранения.

r_Н – номинальное значение плотности электролита аккумулятора при +25 ⁰С;

r_К – заданная плотность электролита аккумулятора, приведенная к температуре +25 ⁰С, при которой его отправляют на заряд; Т– время снижения плотности r_Н до r_К;

t₀ – время постановки аккумулятора на хранение

Рисунок 1 – Характер возможной закономерности изменения плотности

электролита аккумулятора при саморазряде

По результатам экспериментального исследования [1] принимаем допущение, что Т является постоянной величиной. Из-за саморазряда аккумулятора происходит потеря его качества (уменьшается ёмкость, величина тока в стартерном режиме разряда, снижается напряжение и т.п.). Если плотность электролита равна r (r_К
£
r
£r_Н), то за время хранения Dt стоимость аккумулятора по падению плотности электролита уменьшается на h(r)×Dt. В результате в рассматриваемой модели потери начальной стоимости аккумулятора Н на каждом из интервалов to+nT, to+(n+1)T, равны:
t₀+(n+1)T

H=òh(r(t))dt. (1)
t₀+nT

На приведение плотности аккумулятора к номинальному значению (заряд) производят затраты Z, определяемые разовыми затратами, независящими от величины снижения плотности электролита Dr_К = r_Н
- r_К, обозначим их Z₀, и затратами, пропорциональными величинеDr_К, обозначим их С. Тогда стоимость заряда аккумулятора будет равна:

Z=Z₀ + C×Dr_К.

Реально затраты Z₀ связаны с диагностированием аккумулятора, с его техническим обслуживанием, с установкой и снятием с заряда и т.п. Затраты С×Dr_К определяются затратами на заряд аккумулятора.

Дальнейшие исследования, связанные с отысканием оптимального значения разности номинальной и критической плотности электролита аккумулятора, хранящегося с залитым электролитом, удобно производить, базируясь на математическом аппарате теории управления запасами [2].

На основании полученных экспериментальных данных по изменению плотности электролита аккумулятора по времени, обработанных с использованием программного обеспечения по статической обработке «STADIA» [1] , были получены уравнения регрессии вида:

r = r_Н - k×t, (2)

где r – фактическая плотность электролита аккумулятора через время хранения t, приведённая к +25 ⁰С, г/см³;

r_Н
– номинальная для данной природно-климатической зоны эксплуатации плотность электролита аккумулятора, приведённая к +25 ⁰С, г/см³;

k – среднесуточное падение плотности электролита из-за саморазряда аккумулятора, г/см³/сутки;

t – время хранения аккумулятора, сутки.

Рассмотрим общие затраты, необходимые для поддержания плотности электролита аккумулятора r_Н, включая потерю его начальной стоимости Н (физический смысл Н – это потери начальной стоимости аккумулятора в результате его саморазряда за период времени хранения Т, то есть в результате его старения, уменьшающего остаточный ресурс работы аккумулятора). Для корректности и независимости от величины рассматриваемого интервала времени естественно взять составляющие затрат, приведенные к единице времени. Тогда затраты W, приведенные к единице времени равны:

W=Z/T+H/T

Или

W=Z₀/T+C×Dr_К/T+H/T (3)

По результатам экспериментального исследования работ [1, 3] можно записать уравнение:

r = r(t)=r_H+k×t, (4)

где r
– плотность электролита аккумулятора, г/см³, приведенная к температуре +25 ⁰С, после его хранения в течение времени t;

k – коэффициент понижения плотности электролита аккумулятора за время хранения Т.

Уравнение (3) даёт возможность принять:

h(r)=m×Dr_К,

где m – коэффициент потери начальной стоимости аккумулятора при износе Н за период времени Т.

Тогда изменение плотности электролита (ее снижение при саморазряде аккумулятора) имеет вид в соответствии с рисунком 2.

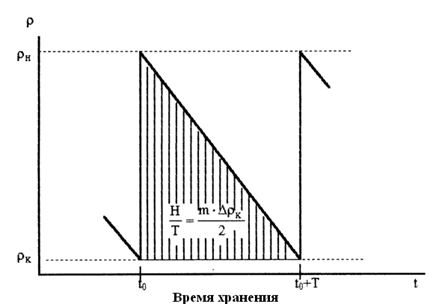
Рисунок 2 – Характер фактической закономерности изменения плотности электролита при саморазряде аккумулятора

Для удобства дальнейших расчетов принимаем:

Dr_К=(r_H-r_К)×100. (5)

Величина периода Т данного процесса определяется по результатам экспериментального исследования работы [1] при условии что t = t₀+n×T как:

T=Dr_К/|k|. (5)

Подставляя отношение (5) и значение 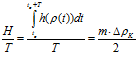 потерь стоимости аккумулятора за единицу времени периода Т, полученные из (1) и зависимости изменения плотности электролита аккумулятора, находящегося на хранении, от саморазряда, представленной на рисунке 2 в выражение (3) получим:

W=(Z₀×k)/Dr_К+C×k+(m×Dr_К)/2. (6)

Для определения оптимального значения Dr_КO исследуем выражение (6) на экстремум. Найдем частную производную W по Dr_К и приравняем ее к нулю:

¶W/¶(Dr_К)=-(Z₀
|k|)/(Dr_К)²+m/2=0.

Отсюда:

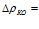
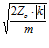 (7)

является критической точкой.

Найдем вторую производную от уравнения (6):

¶²W/¶(Dr_К) = (2Z₀×|k|)/(Dr_К)³.

Так как ¶²W/¶(Dr_К)>0, то Dr_К соответствует минимальному значению W – W₀, при этом:

,

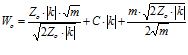Откуда

.

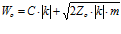Оптимальное значение W₀ достигается при таком Dr_КO, при котором потери, связанные с ухудшением качества аккумулятора (потери начальной стоимости) Н равны разовой независящей от степени заряженности стоимости заряда Z₀.

Из уравнения (7):

Z₀ = (Dr_КO)²×m/2|k|. (8)

Для определения оптимального Dr_К0 необходимо знать величины Z₀, m, k. Однако величину Dr_КO можно оценить исходя из следующих соображений. Разовые затраты Z₀, независящие от Dr_КO тем больше, чем больше коэффициент m (хуже качество аккумулятора) и чем больше период Т между зарядами (требуется большой объем работ по техническому обслуживанию), то есть:

Z₀»b×m×T, (9)

где b – коэффициент, определяющий соотношение между стоимостью

обслуживания и потерями качества аккумулятора за период времени Т.

Коэффициент b математически можно записать в виде:

b=Z/H.

Значения коэффициента b должны лежать в интервале 0£
b
£1.

Если бы оказалось, что b >1, то затраты на поддержание готовности аккумулятора в процессе хранения за период времени Т превышали бы потери его стоимости за тот же период, что свидетельствовало бы о том, что используется экономически нецелесообразная система поддержания готовности аккумулятора к использованию. Подставив значения Т из уравнения (5) в (9) получаем:

Z₀»b×m×Dr_К/|k|.

Преобразуем полученное выше выражение и получим:

Z₀/b»m×Dr_К/|k|. (10)

Подставив (10) в (8), с учетом интервала, в котором должны изменяться значения коэффициента b и принятого ранее условия (5), получаем:

0 £
Dr_КO
£0,02 г/см³.

Краткие выводы

Полученная максимальная величина оптимального допустимого снижения плотности электролита является диагностическим критерием минимальной допустимой степени заряженности аккумулятора [1]. При уменьшении плотности электролита на величинуDr_КO
£0,02 г/см³ общие затраты на поддержание готовности аккумулятора будут минимальными, то есть полученная в ходе исследования величина снижения плотности электролита Dr_КO
£0,02 г/см³, по которой определяется минимальная допустимая степень заряженности аккумулятора, удовлетворяет как требованию продления срока службы хранящихся батарей свыше 5 лет, так и требованию минимальных затрат на поддержание их готовности.

1. Гумелев, В.Ю. Рациональный режим хранения свинцовых стартерных батарей, основанный на результатах исследования процессов старения их аккумуляторов [Текст]: дис. … канд. техн. наук : 20.02.17 : защищена 01.06.01 : утв. 20.07.01 / Гумелев Василий Юрьевич. – Рязань, 2001. – 257 с
2. Вагнер Г.Н. Основы исследования операций. Т.3. – М.: Мир, 1973.-502с.
3. Гумелёв В.Ю. Атомарный состав поверхности электродов свинцовых аккумуляторов. // Исследования в области естественных наук. – № 7 (19) Июль 2013 [Электронный ресурс]. URL: http://science.snauka.ru/2013/07/5207

Все статьи автора «Гумелёв Василий Юрьевич»