Введение
Экспериментальное определение вертикального профиля скорости звука является важным для многих разделов акустики [1, 2]. С одной стороны, этот профиль представляет интерес сам по себе, например, для задач рефракции акустических волн в атмосфере [1, 3]. С другой стороны, профили скорости звука определяются параметрами среды. В частности, в атмосфере это, главным образом, профили температуры и, в незначительной степени, влажности [4], а также различные конвективные движения воздуха. Поэтому оказывается возможным сделать определенные выводы о параметрах среды по измеренному значению вертикального профиля скорости акустической волны. Однако в настоящее время экспериментальное определение этих профилей является достаточно сложной задачей [4, 5].
Определенный интерес представляет подход, основанный на эффекте Доплера в неоднородных средах. В [6] этот подход рассматривался применительно к определению вертикального профиля, главным образом, показателя (индекса) преломления атмосферы. Поэтому в [6] не учитывалось возможное влияние скорости конвективных движений воздуха на результаты измерений (влияние скорости ветра).
В то же время, для скорости звука (которая на шесть порядков ниже скорости света) необходимо различать скорость С0 в неподвижной среде и скорость Сн в среде, движущейся с некоторой скоростью W (относительно неподвижного наблюдателя).
Для весьма широкого круга задач скорость ветра (скорость конвективных движений) важна сама по себе, безотносительно к акустике (метеорология, авиация, высотное строительство, артиллерийские стрельбы и т.д.).
В связи с этим, в данной работе рассматриваются особенности определения вертикального профиля скорости звука с учетом наличия конвективных движений воздуха; возможности одновременного определения вертикального профиля скорости звука и вертикального профиля скорости ветра.
Эффект Доплера в неоднородной среде
При движении источника акустических (или электромагнитных) волн относительно приемника, за счет эффекта Доплера частота p сигнала на выходе приемника отличается от частоты 0 волны, формируемой источником.
Рассмотрим неоднородную (градиентную) среду, для которой изменения скорости волны относительно малы («слабая неоднородность») на пространственном масштабе порядка длины волны : C(z + ) – C(z) << C(z). Пусть источник и приемник движутся относительно среды, причем V(z1) = V1 = dz1/dt; V(z2) = V2 = dz2/dt есть проекции соответствующей скорости на направление распространения волны (линию визирования). Если при этом C/t = 0, то мгновенная частота сигнала имеет вид [6]:
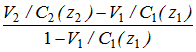 ] .
] .Для многих практически важных задач выполняется условие: V/C << 1. Тогда для относительного сдвига частоты /0 ( - 0)/0 получим:
То есть, сдвиг частоты зависит от «локальных» значений скорости волны C(z1) C1, C(z2) C2. Однако понятие «локальности» требует уточнения. Действительно, любой волновой процесс имеет «внутренний» характерный масштаб, по порядку величины равный длине волны . «Внешний» же масштаб равен расстоянию между источником и приемником. Поэтому «локальность» скорости волны определим следующим образом: если << z2 – z1, то C(z1), C(z2) есть скорость волны, усредненная по пространственному масштабу, по порядку величины равному . Если же z2 – z1, то усреднение следует проводить по масштабу, равному расстоянию z2 – z1 между источником и приемником.
Положим, что некоторый зонд, перемещающийся в атмосфере по вертикали со скоростью V, излучает (переизлучает) модулированную акустическую (или электромагнитную) волну. При этом несущая частота f1 = 1/(2) и частота модуляции
f2 = 1/(2), выбраны такими, что f1 С/h (1 h), а f2 C/H (2 H), где C – средняя скорость волны в исследуемой среде, h - требуемое пространственное разрешение, H - максимальная дальность измерений, 1= C/f1, 2 = C/f2.
Приемник, установленный на земле, регистрирует «сдвинутые» частоты fp1, fp2. Для скорости волны С(z) на высоте z относительные сдвиги частот сигналов, принятых наблюдателем при z = 0, имеют вид:
где Ch – «местная» (локальная) скорость звука, Cс – средняя по трассе скорость звука:
.gif) ; Cс =
; Cс =.gif) .
.Нетрудно видеть, что отношение сдвигов частот определяется только вертикальным профилем скорости волны и не зависит от скорости движения зонда. А поскольку величина h соответствует пространственному разрешению, то положим, что Ch = C(z). Тогда получим:
.gif) =
= .gif) . (1)
. (1)Параметр A есть отношение относительного сдвига частоты модуляции к относительному сдвигу несущей частоты. Для краткости будем далее называть эту величину отношением сдвига частоты модуляции к сдвигу несущей частоты. Эта величина, по сути своей, может быть названа показателем неоднородности скорости звука.
Из (1) следует дифференциальное уравнение:
Его решение имеет вид:
.gif) } A(z) +
} A(z) + .gif) dz, (2)
dz, (2)где C(0) – скорость волны на уровне земли z = 0.
Как показано в [6], при надлежащем исполнении схемы измерений рассматриваемый способ позволяет обеспечить весьма низкие погрешности измерения скорости звука – менее сантиметра в секунду!
Скорость звука и движения воздуха в атмосфере
Скорость звука Сн относительно неподвижного наблюдателя определяется, как известно, не только скоростью звука С0 в неподвижной среде, но и скоростью W движения этой среды относительно того же наблюдателя:
Это соотношение имеет векторный характер, так что W есть проекция скорости движения среды на направление распространения акустической волны («линию визирования»). Скорость W может быть обусловлена различными конвективными потоками воздуха, в том числе, конвективными струями и термиками («теплыми пузырями»). При этом W может быть достаточно высокой, превышая 20 м/с [7].
Для ряда задач физики атмосферы, атмосферной акустики интерес представляет вертикальный профиль Сн, поскольку именно он определяет рефракцию звука. В то же время, и профили С0 важно знать для многих задач теории и практики, в частности, для восстановления вертикальных профилей температуры и влажности воздуха [8].
В общем случае движения воздуха в атмосфере имеют турбулентный характер. Однако описание скорости звука с учетом турбулентности воздуха представляет достаточно сложную задачу. Поэтому мы ограничимся анализом только лишь ламинарных движений.
Выше полагалось, что зонд под действием сил плавучести перемещается по вертикали, причем и линия визирования является вертикалью. Однако под действием ветра зонд может «дрейфовать» в направлении ветра – по горизонтали. При этом линия визирования будет отклоняться от вертикали. Если W0 - полная скорость ветра (по горизонтали), то ее проекция W на «линию визирования» имеет вид: |W| = |W0| cos , где – угол места зонда относительно неподвижного наблюдателя. Знак проекции W определяется очевидными геометрическими соображениями.
Рассмотрим схему измерений, представленную на рис.1 (аналогичную схеме [6]).
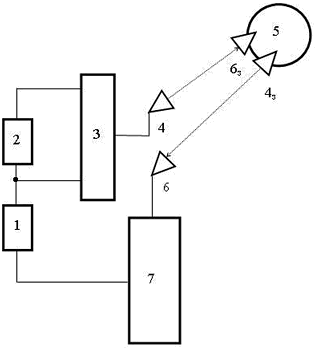 Рис. 1. Функциональная схема измерений
Рис. 1. Функциональная схема измерений
1 – генератор несущей частоты f1; 2 – формирователь частоты модуляции f2; 3 – модулятор; 4 – излучатель; 5 – зонд с дополнительным излучателем 4з и дополнительным приемником 6з; 6 – приемник; 7 – блок обработки сигналов
В данном случае для распространения волны от излучателя 4 к зонду 5 скорость C45 этой волны относительно неподвижного наблюдателя (источника 4 и приемника 6) имеет вид: C45 = С0 + W (знак «+» выбран в определенной мере произвольно). Для распространения волны от зонда 5 к приемнику 6 скорость C56 волны относительно неподвижного наблюдателя имеет вид: C56 = С0 – W (знакиW в выражениях C45 и C56 противоположны друг другу). Тогда результирующий относительный сдвиг произвольной частоты f0 имеет вид:
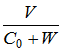 +
+ .gif) =
= .gif) .
.То есть, f/f зависит от скорости ветра W. Эта зависимость будет проявляться как для несущей частоты f1, так и для частоты модуляции f2.
Введем аналогично (1) параметр A, соответствующий суммарному распространению волны «по ветру и против ветра» и учтем, что обычно W << C, причем скорость ветра W зависит от высоты z, W =W(z). Примем также, что Wh – «местная» (локальная) скорость ветра Wh, а Wс – средняя по трассе скорость ветра:
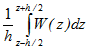 W(z); Wс =
W(z); Wс =.gif) .
.Тогда
Параметр A в (3) аналогичен введенному в (1) параметру A:
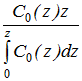 =
= .gif) .
.Нетрудно видеть, что 1 - A = (Cc0 – Ch0)/Cc0 C/C. При этом |1 - A| = |C/C| << 1. В частности, A = 1 в двух случаях: при отсутствии ветра (W = 0) или же при отсутствии градиентов скорости звука (Cс =Ch).
Поскольку A очень слабо зависит от скорости ветра W, то соотношение (2) позволяет найти скорость звука в неподвижной среде: Cс0 = Cс; Ch0 (z) = Ch С0(z) = С(z).
Абсолютные погрешности измерений скорости звука в данном случае будут примерно такими же, как и в [6], составляя всего лишь единицы сантиметра в секунду.
Итак, в данном случае скорость ветра (конвективных потоков) практически не влияет на измерение вертикального профиля скорости звука. В то же время, зная С0, можно сделать определенные выводы о некоторых параметрах атмосферы. Действительно, скорость звука С0 в атмосфере с абсолютной температурой T, как известно, имеет вид:
где – показатель адиабаты, R – универсальная газовая постоянная; – молекулярный вес сухого воздуха; e, p - парциальное давление (упругость) водяного пара и общее давление воздуха соответственно [4]. Для практически важных случаев 0,14 e/p 10-3…10-2 << 1, так что в первом приближении можно считать, что С0 зависит только лишь от температуры воздуха T. Однако полное игнорирование влажности воздуха может привести к заметным погрешностям определения температуры T(z) по измеренным значениям скорости звука. Эти погрешности могут доходить до значительной величины 100 K. По-видимому, лишь при отрицательных температурах, когда даже для насыщенного водяного пара 0,14 e/p < 10-3, эти погрешности не будут превосходить приемлемой для многих задач величины 10-1 K.
Положим теперь, что зонд 5 (рис. 1) снабжен датчиком температуры (то есть, используется «стандартный» метеозонд). Тогда по независимым измерениям скорости звука и температуры можно определить и влажность воздуха. При этом восстановление профиля влажности может быть более простым, чем при использовании традиционных датчиков влажности, особенно, при низких температурах воздуха. Если температура измеряется с погрешностью 3.10-2 K, то погрешность e измерения абсолютной влажности (упругости водяного пара) может составлять всего e = 70 Па. Отметим, что упругость насыщенного водяного пара e = 51 Па при температуре воздуха -300С; e = 125 Па при температуре -200С; e = 287 Па при температуре -100С. То есть, определение влажности воздуха возможно и при достаточно низких температурах воздуха -200С.
Определение вертикальных профилей скорости ветра
Для весьма широкого круга задач скорость ветра (скорость конвективных движений) важна сама по себе, безотносительно к акустике (метеорология, авиация, высотное строительство, артиллерийские стрельбы и т.д.).
Распространенные радиолокационные методы определения вертикальных профилей ветра основаны на слежении за движущимся зондом. Эти методы обычно не применимы на малых высотах (до нескольких сотен метров) вследствие наличия «мертвой зоны» радиолокатора.
Параметр A, как видно из (3), очень слабо зависит от W. Поэтому рассмотрим несколько иные дополнительные измеряемые параметры.
Пусть на зонде 5 (см. рис. 1) установлен дополнительный приемник акустических волн 6з (аналогичный «наземному» приемнику 6), сигнал с этого приемника передается на Землю по радиоканалу (СВЧ-каналу). Буква «з» в обозначении 6з означает «зонд». Тогда сдвиг частоты имеет вид:
.gif) +
+где C00 – скорость электромагнитных волн в атмосфере. Однако скорость света на шесть порядков превосходит звука, C00 >>> C0 + W, поэтому практически (f/f )45 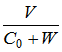 .
.
Рассмотрим теперь параметр A+, соответствующий распространению волны «по ветру». В этом случае C45 = С0 + W. Учтем также, что Cс0 Cс; Ch0 Ch. Тогда получим:
A+ = ![]() =
=![]()
![]() ; (4)
; (4)
Установленный на зонде 5 дополнительный излучатель акустических волн 4з (аналогичный «наземному» излучателю 4) также синхронизируется с Земли по радиоканалу. Тогда соответствующий сдвиг частоты имеет вид:
.gif) +
+ .gif) .
.Рассмотрим теперь параметр A-, соответствующий распространению волны «по ветру». Здесь C56 = С0 - W. Учтем также, что Cс0 Cс; Ch0 Ch. Тогда получим:
A- = ![]() =
=![]()
![]() . (5)
. (5)
В этом случае имеем:
Примем обозначение: ![]() B и учтем, что Wh W = W(z). Тогда из (6) получим:
B и учтем, что Wh W = W(z). Тогда из (6) получим:
.gif) = Cc(
= Cc(Продифференцировав это соотношение по высоте зонда z, получим дифференциальное уравнение для определения вертикального профиля ветра:
где P(z) ![]() , Q(z)
, Q(z) ![]() , D(z) BCc =
, D(z) BCc = ![]() Cc =
Cc =![]() .
.
Для (1), (3) нетрудно найти производную функции A = A:
В атмосфере градиенты скорости звука малы, dC/dz << C/z. Поэтому оценим эти градиенты, полагая для определенности, что C(z) линейно изменяется с высотой, ![]() = const.
= const.
.gif) .
.Тогда получим:
Соответственно, коэффициент P в (7) имеет вид: P = ![]() = -
= -![]() .
.
Рассмотрим теперь величины, входящие в Q(z).
![]() =
= .gif) (
(![]() -
-![]() ) =
) = .gif)
![]() .
.![]() =
= ![]() .
.
Для рассматриваемого случая ![]() = const, как нетрудно видеть, 1 – A = -
= const, как нетрудно видеть, 1 – A = -![]() z. Далее, положим, что малы не только градиенты скорости звука (dC/dz << C/z), но и градиенты скорости ветра: dW/dz<< W/z. Тогда из (6) получим:
z. Далее, положим, что малы не только градиенты скорости звука (dC/dz << C/z), но и градиенты скорости ветра: dW/dz<< W/z. Тогда из (6) получим:
Из последнего соотношения следует, что ![]() =
= ![]() . В этом случае имеем:
. В этом случае имеем:
В результате уравнение (7) сводится к виду:
Решение (8) имеет вид:
.gif)
.gif) , (9)
, (9)где Wz0 = W(z0) – постоянная интегрирования (известная скорость на заданной высоте z0). Отметим, что на высоте z = 0, точнее, в пределах так называемого слоя прилипания, скорость ветра равна нулю, так что обычно z0 составляет 100 м.
С учетом (2) соотношение (9) можно представить в виде:
.gif) }. (10)
}. (10)Учтем, что ![]() << 1. Тогда (10) примет вид:
<< 1. Тогда (10) примет вид:
.gif) . (11)
. (11)В (9)-(11) измеряемыми величинами являются A, A+, A-. Скорость звука C(z) на высоте z вычисляется по соотношению (2). Скорость звука C(z0) на высоте z0, как и скорость ветра W(z0) должны быть известны из независимых измерений. Отметим, что для скорости звука высота z0 может быть практически любой, в том числе, и равной нулю.
В предельном случае W не зависит от высоты z зонда: dW/dz = 0. Тогда из (8) получим:
Оценим теперь возможные погрешности измерения W по (12), полагая, что равны абсолютные погрешности: A = A+ = A- = A. Учтем также, что |1 - A|, |1 – A+|, |1 – A-| << 1.
Тогда получим:
Учтем далее, что 1 - A = C/C; W/C << 1. Тогда выражение для погрешности W/W примет вид:
Окончательно получим:
Погрешность A примем такой же, как в [6]: A 10-6 10-7. Положим для оценок, что C/C 10-3. Это соответствует относительному изменению температуры T/T 2.10-3, что вполне реально для обычных условий тропосферы. Тогда получим: W (10-1 10-2) м/с.
Итак, погрешности измерения скорости ветра W могут составлять десятки, а в лучшем случае – единицы сантиметров в секунду.
Заключение
- Акустическое зондирование атмосферы на основе особенностей эффекта Доплера в неоднородных средах рассмотрено с точки зрения влияния скорости ветра (проекции скорости ветра на линию визирования) на результаты измерений. Показано, что в случае, когда источник и приемник акустических волн расположены на земле, а зонд с пассивным ответом перемещается по вертикали, влияние скорости ветра на измерение скорости звука пренебрежимо мало. То есть, отношение сдвига частоты модуляции к сдвигу несущей частоты (показатель неоднородности скорости звука) весьма слабо зависит от скорости ветра. Но в этом случае практически невозможно сделать какие-либо выводы об этой скорости.
- Для получения значимой информации о скорости ветра предложено использовать зонд с активным ответом (зонд, снабженный источником и приемником акустических волн). В процессе зондирования следует измерять показатель неоднородности скорости звука дополнительно в двух режимах – «по ветру» и «против ветра». В одном из них используются источник, установленный на земле, а приемник – на зонде. В другом режиме – наоборот: приемник, установленный на земле, а источник – на зонде. В этих режимах отношение сдвига частоты модуляции к сдвигу несущей частоты значительно сильнее зависит от скорости ветра, чем в режиме, соответствующем суммарной трассе зондирования «по ветру и против ветра».
- Получено дифференциальное уравнение, позволяющее вычислить вертикальный профиль скорости ветра (проекции скорости на линию визирования – направление распространения акустической волны) по измеренным значениям отношения сдвига частоты модуляции к сдвигу несущей частоты в трех режимах: «по ветру», «против ветра», на суммарной трассе «по ветру и против ветра».
- При сравнительно несложном исполнении аппаратуры оказывается возможным одновременное определение вертикального профиля скорости звука и вертикального профиля скорости ветра. При этом можно обеспечить малые погрешности измерений: скорости звука – 100 см/с; скорости ветра – 101 см/с.
- По профилю скорости звука можно вычислить профиль температуры, что особенно важно для зонда с пассивным ответом. Погрешность определения температуры уменьшается с уменьшением абсолютной влажности воздуха, и при отрицательных температурах не будет превосходить приемлемой для многих задач величины 10-1 K. В то же время, возможно использование «стандартного» метеозонда, снабженного датчиком температуры. Тогда по независимым измерениям скорости звука и температуры можно определить и абсолютную влажность воздуха. При этом восстановление профиля влажности может быть более простым, чем при использовании традиционных датчиков влажности, особенно, при низких температурах воздуха (-200С).
Библиографический список
- Исакович М.А. Общая акустика. – М.: Наука, 1973. – 496 с.
- Красильников В.А. Введение в акустику. – М.: Изд-во МГУ, 1992. – 152 с.
- Блохинцев Д.И. Акустика неоднородной движущейся среды. – М.: Наука, 1981. – 208 с.
- Каллистратова М.А., Кон А.И. Радиоакустическое зондирование атмосферы. – М.: Наука, 1985. – 197 с.
- Красненко Н.П. Акустическое зондирование атмосферы. – Новосибирск: Наука, 1986. – 169 с.
- Kolomiets, S.M. Sounding of ocean and atmosphere using Doppler effect in inhomogeneous media / Physics of Wave Phenomena, 2003. – Vol. 11, Number 3 – Pp. 159-167.
- Хромов С.П., Мамонтова Л.И. Метеорологический словарь. – Л.: Гидрометеоиздат, 1974. – 568 с.
- Коломиец С.М. Определение температуры и влажности воздуха по синхронным измерениям скорости звука, индекса преломления и давления / Метеорология и гидрология, 2004. – № 2. – С. 48-56.


