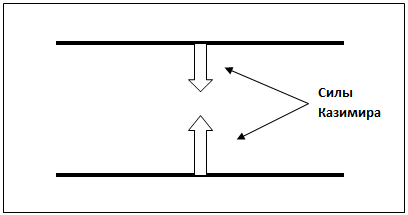
В 1948г Г. Казимир теоретически предсказал эффект, названный позднее его именем [1]. Эффект заключается в том, что на каждую из двух размещённых напротив друг друга плоских, параллельных, проводящих пластин в вакууме, по нормали к ним, действуют силы не гравитационного происхождения, стремящиеся их сблизить (рис 1).
Современное объяснение появления этих сил заключается в том, что они вызываются разницей в давлении виртуальных фотонов на пластины снаружи и изнутри. Согласно законам квантовой механики, между пластинами могут существовать фотоны только с такими длинами волн, которые кратно укладываются в зазоре между пластинами. Т.о., в зазоре «выедается» основная часть виртуальных фотонов, присутствующих в свободном пространстве, и имеющих произвольные длины волн. В результате, давление на пластины снаружи существенно превышает давление изнутри что и вызывает появление силы Казимира.
2. Сила Казимира для 2-х плоских проводящих поверхностей, на единицу площади, равна:
, (1)
где «-» означает, что наблюдается притяжение пластин друг к другу, – постоянная Планка, c – скорость света, а d – расстояние между пластинами [2].
Численно Fc [дин]= 1.3*10-18 * S/d4 , где S и d измеряются в [см]. Например, для пластин площадью 1 см2 и d= 10 нм, сила составит примерно 106 дин, т.е. давление на пластины будет порядка атмосферного !
Величина силы Казимира подтверждена в экспериментах, начиная 1958 г. [3] и совпадает с теоретическим значением для широкого спектра геометрий: плоские пластины, пластина и сфера, два цилиндра, наноконструкции и пр. (см. например, номера 7-15 в списке литературы к [4] и номера 13-21 в списке литературы к [5]).
На сегодня точность экспериментов доведена до процентов от теоретических значений, что неоспоримо подтверждает существование силы Казимира, как физического явления, а также правильность вычисления её величины.
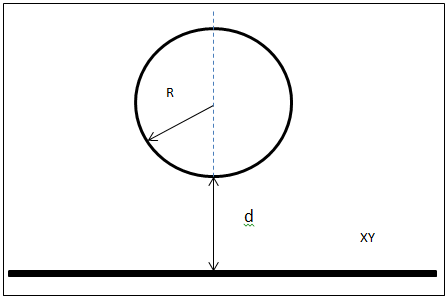
3. Для изучения свойств силы Казимира, в частности, активно используется геометрия «сфера + плоскость» (рис 2), [4], [5], [6].
Теоретическое значение силы Казимира для сферы и плоскости (для случая d << R) даётся выражением [5].:
*R (2).
Эта формула м.б. получена из (1) при самых общих и естественных приближениях, известных, как PFA (Proximity Force Approximation), или PAA (Pairwise Additive Approximation), способ расчёта [5], [6].
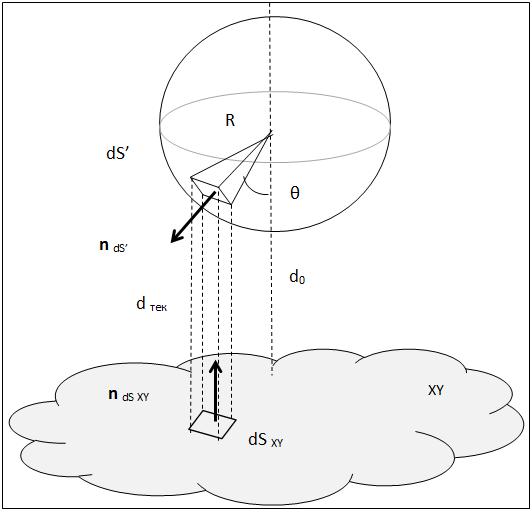
Используя стандартный способ интегрирования по сфере, бесконечно малый элемент её поверхности , заменяем бесконечно малым, считающимся в силу размеров плоским, 4-х угольником
, с нормалью, направленной по радиусу под углом
к оси Z. Вся сфера рассматривается как тело, образованное бесконечным числом таких бесконечно малых 4-х угольников. По естественным причинам рассматривается только нижняя полусфера сферы «С», т.е. диапазон углов:
= [0…π/2] и
= [0…2π).
Каждый элемент проецируется на плоскость, параллельную плоскости XY в элемент
. Далее, используя выражение (1), производится вычисление силы, рассматривая в качестве пластин элемент
и равный ему по площади элемент dSXY плоскости XY под ним. Расстояние dtek равно расстоянию между плоскостью XY и текущим элементом
и, т.о., изменяется от d0 до d0+R. Направление силы Казимира - по нормали к элементу
, т.е. под углом
наружу (рис 3).
После интегрирования (и вводя ограничение d<<R) получаем простое аналитическое выражение для силы Казимира между сферой и плоскостью (2).
Необходимо отметить, что условие d<<R используется всего лишь для получения компактного аналитического выражения, т.е. для упрощения расчётов и дальнейшей аналитики, а не как физическое ограничение, влияющее на свойства или сам факт существования силы Казимира в этой геометрии.
Отметим также тот важный факт, что из бесконечного числа элементов этой полусферы, всего лишь ОДИН, а именно элемент, находящийся в нижней её точке, параллелен плоскости XY. Т.о., только для одного элемента соблюдается геометрия плоскопараллельных пластин исходного эффекта Казимира.
4. Эксперименты с разными геометриями демонстрирует присутствие в них сил, сравнимых по порядку величины с силами Казимира для плоскопараллельных пластин сравнимых размеров. Это прямо указывает на то, что сила Казимира существует и имеет близкую «интенсивность», как между параллельными, так и между непараллельными поверхностями, т.е., по большому счёту - всегда и везде.
Как для геометрии «сфера + плоскость», так и для других геометрий, величины измеренных сил Казимира оказались равны рассчитанным с точностью до 1%, например [7].
Т.о., опираясь на эксперименты, можно резюмировать, что сила Казимира, между сферой и плоскостью существует и может быть корректно вычислена с использованием выражения (2),
Сама формула (2) является прямым следствием применения (1) к поверхностям, обладающим кривизной и расположенным под произвольными углами друг к другу. Последнее следует из того факта, что в геометрии «сфера + плоскость» угол нормали к элементу j изменяется в диапазоне:
= [0…π/2], относительно оси Z, которая является нормалью к плоскости XY.
Т.о., совпадение результатов ряда экспериментов с расчётами, произведёнными по (2), доказывает принципиальную применимость выражения (1) для вычисления сил Казимира в произвольных геометриях.
5. Теперь зададимся вопросом о направлении сил Казимира в геометрии плоских, но не параллельных пластин.
Как отмечено выше, выражение (1) работает в случае произвольной геометрии и кривизны, следовательно, оно работает и в простейшем случае: в случае плоскостей, расположенных под произвольным углом друг к другу.
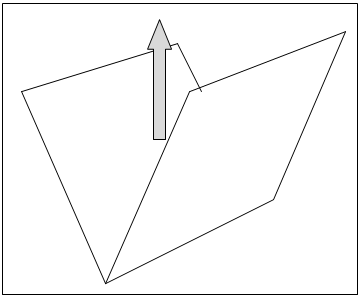
Расположим пластины следующим образом: по одной из одноимённых сторон приведём их в соприкосновение, а противоположные стороны – разведём в стороны (рис 4). Мы получили конструкцию «уголок». Это конструкция, напоминает в плане букву «V» и имеет произвольную длину «вглубь» рисунка.
Сила Казимира является результатом воздействия виртуальных фотонов на площадку dS. При абсолютно упругом ударе (чем и является отражение фотона) меняется только нормальная составляющая импульса Pфотон, а тангенциальная составляющая остаётся неизменной. Т.о., вектор переданного площадке dS импульса Pс направлен по нормали к поверхности. Отметим также тот факт, что направление движения фотона: сверху вниз, или снизу вверх не влияет на направление импульса Pс (рис. 5).
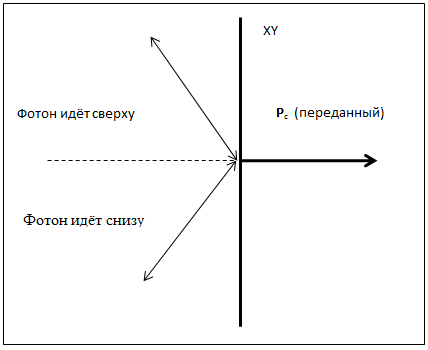
Рис.5. Импульс передаётся всегда в одном направлении, независимо от направления движения фотонов: снизу вверх, или сверху вниз.
Учитывая все рассмотренные факты и выводы из них, мы приходим к заключению, что на каждую плоскость, образующую данную конструкцию «V», «уголок»:
1. Действует сила Казимира – полностью аналогично тому, как она действует на любой элемент сферы , не параллельный плоскости XY.
2. По причинам, указанным выше, сила действует на каждую плоскость по нормали к ней и направлена внутрь «уголка».
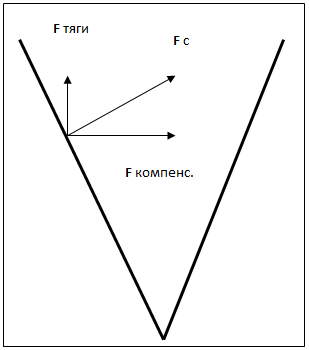
Проведя разложение сил Казимира Fc (действующих на каждую из пластин) на составляющие Fx и Fz , мы видим, что:
- х-составляющие сил, приложенных к пластинам уголка, равны, и направлены навстречу друг другу. Т.о., они являются чистой силой Казимира и стремятся сблизить пластины.
- z-составляющие сил СУММИРУЮТСЯ, что приводит к появлению некомпенсированной силы вдоль оси z (рис. 6).
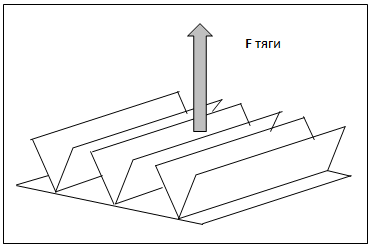
Т.о., мы пришли к выводу, что на «уголок» вдоль оси z действует постоянная сила, создаваемая давлением на эту макро конструкцию виртуальных частиц (в данном случае – фотонов) и эта сила направлена от вершины «уголка» к его раствору.
Далее будем называть эту силу – «сила тяги» (Fтяги).
6. Т.к. новые эффекты следует оценить с точки зрения их соответствия законам сохранения, необходимо сразу и определённо отметить, что существование силы тяги не нарушает этих законов.
Дело в том, что мы рассматриваем, безусловно ОТКРЫТУЮ систему, для которой «уголок» является лишь одной из её частей и, сам по себе, не создаёт никаких сил.
Появление Fтяги обусловлено взаимодействием уголка с виртуальными фотонами, т.е. с вакуумом фотонов Вселенной, которые (виртуальные фотоны) всегда существуют в пространстве и не могут быть экранированы полностью в принципе.
Чтобы снять затруднения в понимании сути полученного результата, достаточно указать на практически полную аналогию в принципе действия описанной конструкции и обычного паруса. Обе эти конструкции являются всего лишь препятствиями, специальным образом сконструированными и размещёнными в пространстве, где существует внешнее по отношению к ним движение материальных элементов.
Эти внешние элементы обладают энергией и импульсом, которые обусловлены глобальными процессами, законами и взаимодействиями, носящими полностью независимый характер по отношению к такому частному явлению, как размещение уголка, или паруса в данной точке пространства-времени.
Т.о., возникающая сила, приложенная к преграде (парусу или уголку), является следствием давления внешних элементов на преграду и не нарушает никаких законов сохранения.
Итак, уголок является конструкцией, преобразующей движение виртуальных фотонов в управляемое по вектору и тяге движение макротела, т.е. управляемым движителем.
7. Вычисляя силу тяги «уголка» при помощи (1), в PFA приближении, (пункт 3), получаем:
) (3)
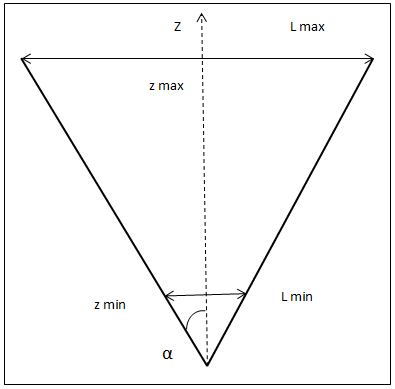
где b – «длина» уголка (буквы V «вглубь» страницы), Lmin - расстояние между сторонами уголка по уровню Zmin, Lmax - расстояние между сторонами уголка по уровню Zmax . Как конкретно измеряются эти величины показано на рис. 7.
Данная формула работает в диапазоне углов: 0<α<(π/4). При α= 0 она переходит в выражение (1) для плоскопараллельных пластин, а при углах α>=(π/4) приближение PFA для этой геометрии не работает.
В силу зависимости Fтяги от ) очевидно, что величина параметра Lmax, фактически, не играет роли, т.к. Lmax >> Lmin.
Т.о., для практических расчётов и оценок, мы имеем следующее выражение (принимая α~0):
Fтяги [дин] ~ 217 * b / (Lmin)3, где b измеряется в [см], а Lmin в [нм].
Величина Lmin ограничена снизу уровнем «обрезания», который определяется технологически:
- точностью изготовления пластин (их шероховатостью, степенью плоскостности), а также
- МИНИМАЛЬНОЙ длиной волны фотонов, которые может эффективно отражать вещество, из которого изготовлен уголок.
Особое внимание следует обратить на то, в силу зависимости Fтяги от (), сила тяги ЧРЕЗВЫЧАЙНО чувствительна к самому незначительному изменению Lmin.
Изменение в (3) других технологических параметров, т.е.:
- увеличение коэффициента отражения поверхностей и/ или расширение диапазона эффективности отражателя в область высоких частот и
- увеличение суммарной длины «уголка» (параметра «b» – длины буквы V «вглубь страницы»),
будут увеличивать Fтяги линейно.
8. Для понимания того, где мы находимся (технологически) в данный момент, можно отметить, что передовые, но не уникальные современные технологии микроэлектроники, при соответствующей доработке, скорее всего смогут создать панели-движители габаритами метр на метр и незначительной толщины, тяга которых будет составлять единицы- десятки дин, что вполне позволяет использовать их как движители малой тяги для космических конструкций.
Панель (в плане), скорее всего, будет выглядеть как сборка уголков: «VVV…VVV», а сам движитель – как набор таких панелей, закреплённых на управляемых независимых подвесах (рис. 8).
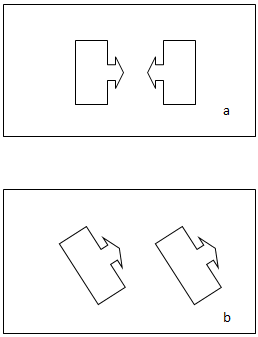
Отметим, что для полного управления вектором и тягой созданного устройства будет достаточно двух одинаковых панелей (рис. 9).
Рис.9. Принцип управления конструкцией на основе панелей с «уголками»: a – движение отсутствует, b – движение в произвольном направлении
Для оценки силы тяги уголка используем следующие значения:
- материал: алюминий (Al), плотность ρ= 2.69 [г/см3],
- угол полураствора уголка, α - минимальный, единицы угловых градусов,
- максимальный раствор уголка, Lmax >> Lmin,
- длина стороны уголка (длина одного из отрезков, образующих букву V), L>~ 100 [мкм],
- уголок заполняет всю возможную площадь панели размером 1[м] х 1[м] (рис. 8) таким образом, что расстояние между одноименными элементами параллельных уголков равно 200 [мкм]. Т.о., его суммарная длина составляет b= 500 000 [см] (5 км),
- минимальная длина волны фотонов эффективно отражаемых поверхностью уголка (Al), λmin= 200 [нм] и, т.о. Lmin =200 [нм],
- коэффициент отражения поверхности (Al) на длине волны λmin= 200 [нм]: R= 0.8,
В результате мы получаем Fтяги~ 10 [дин].
Уменьшение Lmin до 50 [нм] (при значении R~ 0.2) обеспечит силу тяги Fтяги~ 170 [дин].
Если же Lmin удастся довести до 10 [нм], имея при этом коэффициент нормального отражения R~ 0.1, это позволит получить Fтяги~ 11 000 [дин].
Оценивая ускорение ненагруженной панели, имеем следующие величины (при массе панели ~ 700г, размерах 1 м * 1 м * 0.5 мм, коэффициенте пустотелости= 0.5, материале - Al):
- Lmin = 200 [нм]: ускорение a= 0.016 [см/с2],
- Lmin = 50 [нм]: ускорение a= 0.24 [см/с2],
- Lmin = 10 [нм]: ускорение a= 16 [см/с2]= 0.016 [g].
9. Качественное подтверждение рассматриваемого эффекта в эксперименте, может быть получено достаточно просто и быстро в результате проведения измерений тяги «уголка», закрепляемого в разной ориентации на крутильных весах.
10. Эффект Казимира является макроскопическим результатом существования виртуальных фотонов. Таким же статусом существования обладают и все прочие виртуальные частицы – как массовые, так и безмассовые.
В связи с этим представляет значительный интерес экспериментальное изучение аналогов эффекта Казимира для других полей и частиц. Особенно интересна оценка возможности получения силы тяги и её технологически достижимая величина.
Этот интерес объясняется очевидным предположением, что сила тяги, создаваемая массивными частицами, может оказаться существенно больше, чем сила тяги, создаваемая безмассовыми виртуальными фотонами.
11. Практическое применение движителей на основе панелей с «уголками» очевидно: от выработки энергии (при размещении их на валу обычного электрогенератора) (рис. 10), до создания собственно тяговых движителей для перемещения конструкций и аппаратов (самолёты, ракеты, летающие платформы, космические корабли, океанские надводные и подводные суда, средства передвижения, в т.ч. и миниатюрные персональные).
Библиографический список
- H.B.G. Casimir, On the attraction between two perfectly conducting plates // Proc. K. Ned. Akad. Wet. 51, p.793–796 (1948).
- Y. Aulin, Casimir-Lifshitz forces // Univer. of Groningen, pp. 1-21, (May 2009)
- M.Y. Spaarnay, Measurements of attractive forces between flat plates // Physica, V.24, p.751 (1958)
- H.B. Chan et al., Measurement of the Casimir Force between a Gold Sphere and a Silicon Surface // Phys.Rev.Lett., 101 (2008) 030401
- F. Intravaia et al., Strong Casimir force reduction through metallic surface nanostructuring // Nature Comm, art. 2515, 4 (Sep. 2013) pp. 1-20
- A.W. Rodriguez, F. Capasso, S.G. Johnson, The Casimir effect in microstructured geometries // Nature Photonics, V.5, (Apr. 2011), p.211-221
- G. Bressi et al., Measurement of the Casimir Force between Parallel Metallic Surfaces // Phys.Rev.Lett. 88 (2002) 041804