При публикации данной статьи на сайте журнала возможны искажения отображения формул.
Оригинал статьи в формате PDF доступен для скачивания
УДК 539.124.6:539.189.2:541.6:621.382
Е.П.Прокопьев: НИЦ «Курчатовский институт», ФГБУ «ГНЦ РФ ИТЭФ»
Адрес: ул. Б.Черемушкинская, 25, Москва, Россия, 117218
Аннотация
Важнейшей проблемой физики медленных позитронов является построение строгой теории аннигиляции в кристаллических твердых телах. В данном обзорном исследовании проанализирована проблема многих электронов и позитронов в твердом теле с помощью перехода от вторичного квантования к конфигурационному представлению по методу Фока. Рассмотрены методы расчетов стационарных состояний систем из 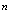 электронов и
электронов и 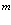 позитронов во внешнем поле и поле кристаллической решетки и вероятностей аннигиляционных переходов в этих внешних полях. Для этого в приближении метода Хартри-Фока рассмотрена задача электронов и позитронов в поле кристаллической решетки. Сформулирована проблема многих электронов и позитронов в твердом теле с помощью метода вторичного квантования.
позитронов во внешнем поле и поле кристаллической решетки и вероятностей аннигиляционных переходов в этих внешних полях. Для этого в приближении метода Хартри-Фока рассмотрена задача электронов и позитронов в поле кристаллической решетки. Сформулирована проблема многих электронов и позитронов в твердом теле с помощью метода вторичного квантования.
Рассмотрены свойства блоховских состояний электронов, позитронов и дырок в поле кристаллической решетки с учетом их взаимодействия. Особое внимание уделено проблемам экситонов, атома 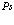 и позитрон-экситонных комплексов.
и позитрон-экситонных комплексов.
Введение
Важнейшей проблемой физики медленных позитронов является построение строгой теории аннигиляции в кристаллических твердых телах (см., например, [1]). Поэтому в данном исследовании сформулируем проблему многих электронов и позитронов в твердом теле с помощью перехода от вторичного квантования к конфигурационному представлению по методу Фока [2], использованного работах [3-7].
Вначале приведем методы расчетов стационарных состояний систем из 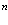 электронов и
электронов и 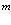 позитронов во внешнем поле и поле кристаллической решетки [4] и вероятностей аннигиляционных переходов в этих внешних полях [3,8].
позитронов во внешнем поле и поле кристаллической решетки [4] и вероятностей аннигиляционных переходов в этих внешних полях [3,8].
1. Квантовополевая теория системы многих электронов и позитронов в твердом теле Известно, что связь между конфигурационным пространством и вторичным квантованием по Фоку [2] дается следующим образом. Гамильтониан с неопределенным числом частиц в рамках метода вторичного квантования имеет вид [4]
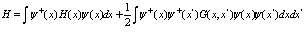 , (1)
, (1)
где 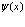 и
и 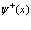 – операторы уничтожения и рождения фермиевского поля. Они удовлетворяют следующим перестановочным соотношениям
– операторы уничтожения и рождения фермиевского поля. Они удовлетворяют следующим перестановочным соотношениям
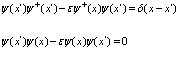 (2)
(2)
Здесь 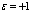 соответствует случаю бозонов, а
соответствует случаю бозонов, а 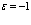 – фермионов. В том случае, если оператор числа частиц
– фермионов. В том случае, если оператор числа частиц
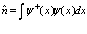 (3)
(3)
диагонален, то операторы 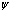 и
и 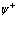 имеют не равные нулю матричные элементы
имеют не равные нулю матричные элементы 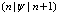 и
и 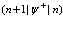 , где
, где
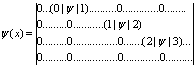 (4)
(4)
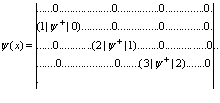 (5)
(5)
Вектор состояния по Фоку, на который действуют операторы рождения и уничтожения частиц 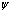 и
и 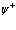 имеет вид
имеет вид
 , (6)
, (6)
где каждый элемент столбца представляет собой волновую функцию Шредингера в пространстве с определенным числом частиц
Выпишем действие операторов 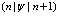 и
и 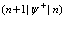 по Фоку на волновую функцию
по Фоку на волновую функцию 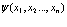
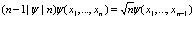 , (6)
, (6)
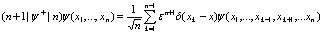 , (7)
, (7)
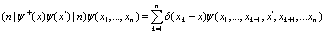 , (8)
, (8)
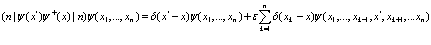 , (9)
, (9)
Квантованное уравнение движения имеет вид
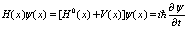 (10)
(10)
Здесь 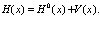
Именно из этого уравнения можем получить уравнение Шредингера в конфигурационном пространстве для системы с определенным числом частиц. Гамильтониан взаимодействия электронов во внешнем поле равен
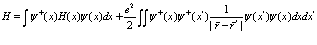 (11)
(11)
Из выражения (11) находим энергию системы с определенным числом частиц 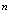 .
.
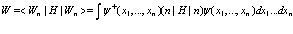 (12)
(12)
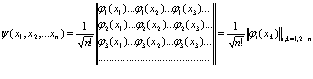 (13)
(13)
Таким образом
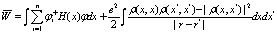 (14)
(14)
Минимизируя функционал 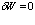 с учетом ортонормированности
с учетом ортонормированности
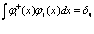 (15)
(15)
получаем уравнения Фока
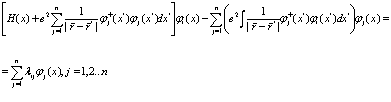 (16)
(16)
Выражение (16) и есть уравнения Фока в конфигурационном пространстве в произвольном внешнем поле. Использование этих уравнений (наиболее строгих) в проблеме твердого тела чрезвычайно затруднено. Полезно изложить основные черты математического формализма получения этих уравнений для систем со многими позитронами и электронами в конденсированных средах и твердом теле в приближении метода Хартри-Фока [5].
Для этого изложим формализм вторичного квантования, обычно проводимый в два этапа. Для этого вначале рассмотрим «классическое поле», а затем его квантование. В качестве классического волнового уравнения выбираем уравнение Шредингера
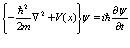 (17)
(17)
и комплексно сопряженное ему уравнение
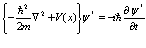 (18)
(18)
Выпишем функцию Лагранжа, а также уравнение Лагранжа, которые приводят к уравнениям (17) и (18)
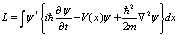 (19)
(19)
Отсюда следует
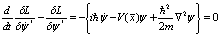 , (20)
, (20)
то есть это просто уравнения (17) и (18).
Канонически сопряженный импульс 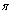 введем как произвольную функцию Лагранжа
введем как произвольную функцию Лагранжа
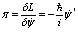 , (21)
, (21)
Таким образом, получаем функцию Гамильтона из функции Лагранжа посредством соотношения
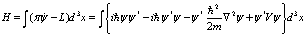 (22)
(22)
Отсюда находим явный вид первично квантованной функции Гамильтона
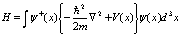 , (23)
, (23)
Заметим, что в данном случае волновые функции 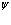 и
и 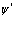 представляют собой «классические поля». Разложим амплитуду поля по собственным функциям волнового уравнения Шредингера
представляют собой «классические поля». Разложим амплитуду поля по собственным функциям волнового уравнения Шредингера
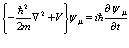 (24)
(24)
Эти функции записываются в виде
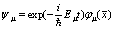 (25
(25
Отметим, потенциал 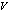 не зависит от времени.
не зависит от времени.
Разложим теперь волновую функцию 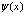 по этим собственным функциям
по этим собственным функциям 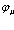 . Запишем временной множитель в виде
. Запишем временной множитель в виде
 (26)
(26)
Отсюда разложение волновых функций 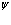 и
и 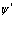 принимают следующие значения
принимают следующие значения
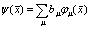 , (27)
, (27)
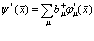 , (28)
, (28)
Полезно напомнить, как получаются перестановочные соотношения для амплитуд 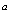 . Для этого введем вакуумное состояние
. Для этого введем вакуумное состояние 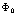 и
и 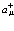 – оператор рождения. Тогда формально можно создать две частицы в одном и том же состоянии
– оператор рождения. Тогда формально можно создать две частицы в одном и том же состоянии 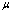 через
через 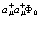 . Естественно, что
. Естественно, что
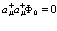 (29)
(29)
Требование (29) должно соблюдаться не только для 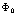 , но и для любого
, но и для любого 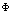 , так что
, так что
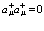 (30)
(30)
Отсюда легко постулируются перестановочные соотношения для ферми-частиц для амплитуд поля
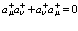 , (31)
, (31)
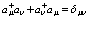 , (32)
, (32)
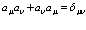 , (33)
, (33)
Так как полевые операторы 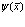 и
и 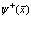 связаны с операторами
связаны с операторами 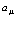 и
и 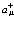 через разложения (27), (28), то перестановочные соотношения (31)-(33) имеют своим следствием перестановочные соотношения для
через разложения (27), (28), то перестановочные соотношения (31)-(33) имеют своим следствием перестановочные соотношения для 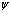 и
и 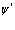 вида (2) и наоборот.
вида (2) и наоборот.
Таким образом, оператор Гамильтона оказывается равным
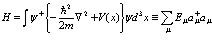 (34)
(34)
При этом уравнение Шредингера для квантованного состояния имеет вид
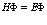 , (35)
, (35)
причем
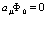 (36)
(36)
и
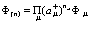 (37)
(37)
Энергия 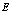 дается выражением
дается выражением
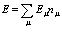 , где
, где 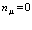 или
или 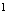 (38)
(38)
Полное число частиц равно
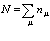 (39)
(39)
Далее рассмотрим наиболее общее одночастичное состояние, задаваемое суперпозицией одночастичных состояний
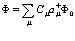 (40)
(40)
причем 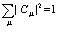 является еще произвольным. Перейдем вновь к представлению состояния
является еще произвольным. Перейдем вновь к представлению состояния 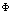 . Очевидно, что
. Очевидно, что
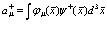 (41)
(41)
Подставляя (41) в (40), получаем
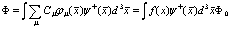 (42)
(42)
Функция 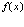 удовлетворяет обычному одночастичному уравнению Шредингера. Далее подставим одночастичные функции (42) во вторично квантованное уравнение Шредингера (35). Имеем
удовлетворяет обычному одночастичному уравнению Шредингера. Далее подставим одночастичные функции (42) во вторично квантованное уравнение Шредингера (35). Имеем
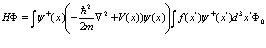 (43)
(43)
С учетом перестановочных соотношений
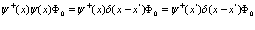
получаем из (43)
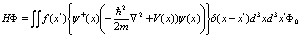 (44)
(44)
Это выражение преобразуется к виду
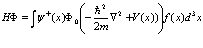 (45)
(45)
Легко видеть, что
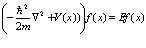 (46)
(46)
Теперь рассмотрим наиболее общее состояние двух частиц
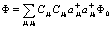 (47)
(47)
Как и ранее
 (48)
(48)
Причем
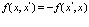 (49)
(49)
Выберем
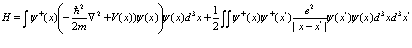 (50)
(50)
Тогда нетрудно показать, что функция 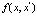 удовлетворяет уравнению Шредингера для двух частиц
удовлетворяет уравнению Шредингера для двух частиц
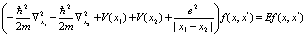 (51)
(51)
Можно легко обобщить этот результат для 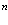 частиц
частиц
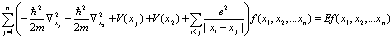 (52)
(52)
Развитый выше формализм позволяет нам сформулировать задачу и для системы 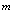 нерелятивистских позитронов.
нерелятивистских позитронов.
Рассмотрим теперь систему из 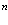 электронов и
электронов и 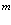 позитронов в кристаллической решетке твердого тела в приближении Хартри-Фока.
позитронов в кристаллической решетке твердого тела в приближении Хартри-Фока.
2. Электроны и позитроны в кристаллической решетке: формулировка проблемы многих тел. Приближение Хартри-Фока
Сформулируем проблему многих электронов и позитронов в твердом теле с помощью метода вторичного квантования. Представим себе следующую картину: электроны и позитроны движутся в строго периодической решетке, ионы которой имеют бесконечно тяжелые массы. Иными словами можно считать, что они находятся в состоянии покоя. Принимаем далее, что электроны внутренних атомных оболочек учитываются в целом тем, что они вместе с положительно заряженными атомными ядрами создают эффективный, периодический с периодом решетки потенциал 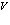 .
.
Естественно, что позитроны в основном движутся по периферии атомов кристалла в силу электростатического отталкивания ядер. Оператор Гамильтона для электронов и позитронов состоит из четырех частей: кинетической энергии электронов (позитронов), потенциальной энергии взаимодействия между электронами (позитронами), кулоновской энергии взаимодействия между электронами (позитронами) и кулоновского взаимодействия электронов с позитронами. Соответствующее уравнение Шредингера будет иметь вид
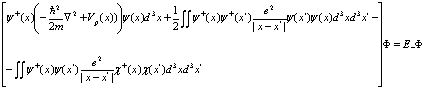 (53)
(53)
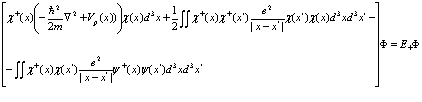 (54)
(54)
Причем функции 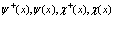 являются операторами, удовлетворяющими ферми-перестановочным соотношениям типа (31)-(33). Разложим эти операторы по собственным функциям
являются операторами, удовлетворяющими ферми-перестановочным соотношениям типа (31)-(33). Разложим эти операторы по собственным функциям 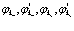
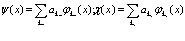 (55)
(55)
 (56)
(56)
Принимаем, что собственные функции 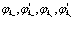 образуют полный набор ортонормированных функций, но их следует оптимизировать так, чтобы они являлись решениями уравнения Щредингера. Для этого используем метод Хартри-Фока, уже описанный выше.
образуют полный набор ортонормированных функций, но их следует оптимизировать так, чтобы они являлись решениями уравнения Щредингера. Для этого используем метод Хартри-Фока, уже описанный выше.
Создадим некоторое состояние 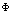 электронов и позитронов кристалла. Для этого следует расположить электроны и позитроны один за другим по состояниям
электронов и позитронов кристалла. Для этого следует расположить электроны и позитроны один за другим по состояниям 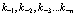 и
и 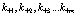 . Таким образом
. Таким образом
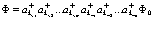 (57)
(57)
Используем эту функцию для построения среднего значения оператора Гамильтона 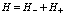 (см.(53) и (54)) с дополнительным условием, что функция состояния нормирована. Далее требуем условия
(см.(53) и (54)) с дополнительным условием, что функция состояния нормирована. Далее требуем условия
 (58)
(58)
с дополнительным условием
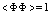 (59)
(59)
и вычислим выражение (58) как функционал 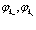 . Затем определяем
. Затем определяем 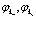 с помощью варьирования.
с помощью варьирования.
Для этого подставим (55) и (56) в (53) и (54). Поскольку операторы 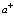 и
и 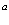 не зависят от интегрирования, волновые функции
не зависят от интегрирования, волновые функции  коммутируют с операторами, то операторы можно вынести за знак интеграла. Тогда выражение для оператора Гамильтона принимает вид
коммутируют с операторами, то операторы можно вынести за знак интеграла. Тогда выражение для оператора Гамильтона принимает вид
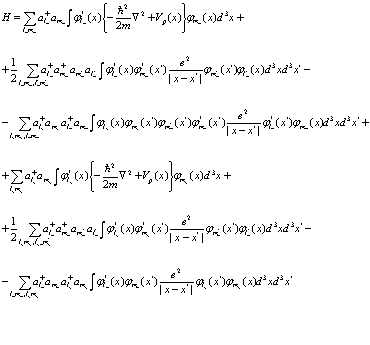 (60)
(60)
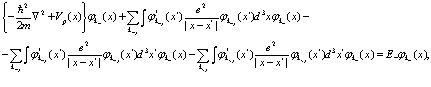
Далее следует построить среднее значение этого Гамильтониана на функциях состояния (55), (56). Используя метод Хакена [4], сразу же получаем
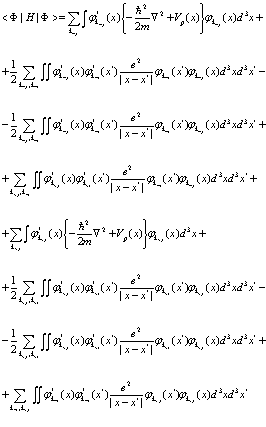 (61)
(61)
Здесь суммирование распространяется только на занятые состояния 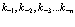 и
и 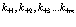 .
.
Условие нормировки используется, как обычно, в качестве дополнительного условия
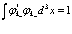 ;
; 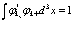 (62)
(62)
Для этого применим обычным образом параметр Лагранжа, который обозначим через 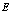 . Проведение варьирования
. Проведение варьирования  и
и 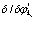 приводит сразу же к уравнениям
приводит сразу же к уравнениям
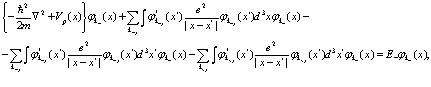 (63)
(63)
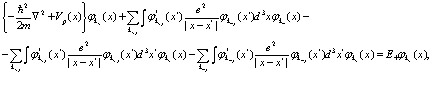 (64)
(64)
Для интерпретации уравнений самосогласованного поля (63) и (64) рассмотрим входящие в него отдельные члены.
Первые члены в фигурных скобках в уравнениях (63), (64) представляют потенциальную и кинетическую энергию электронов и позитронов в периодической решетке кристалла соответственно. Следующие выражения в уравнениях (63), (64) представляют представляют произведения искомых функций 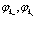 и сумм по
и сумм по 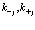
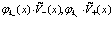 (65)
(65)
Здесь
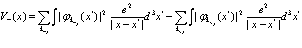 (66)
(66)
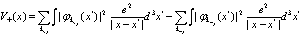 (67)
(67)
Так как 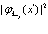 и
и 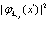 имеют смысл плотности заряда для электронов и позитронов, то суммы по
имеют смысл плотности заряда для электронов и позитронов, то суммы по 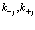 имеют смысл электростатических потенциалов электронов и позитронов в состояниях
имеют смысл электростатических потенциалов электронов и позитронов в состояниях 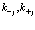 .
.
Предпоследние члены в уравнениях (63), (64) имеют вид
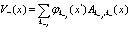 (68)
(68)
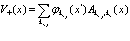 (69)
(69)
где
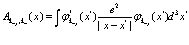 , (70)
, (70)
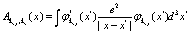 (71)
(71)
Выражения (68)-(71) характеризуют так называемое обменное кулоновское взаимодействие .
Таким образом, можем записать уравнения (63), (64) в виде
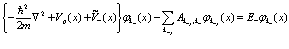 (72)
(72)
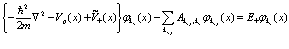 (73)
(73)
В реальных условиях экспериментов концентрация позитронов составляет величину ~ 1 см-3, поэтому уравнение (73) существенно упрощается
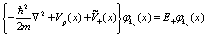 (74)
(74)
Здесь
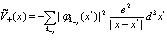 (75)
(75)
Уравнение Шредингера вида (72) и (73) можно записать в краткой форме
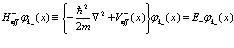 (76)
(76)
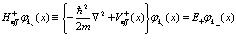 (77)
(77)
В общем случае можно утверждать, что потенциалы 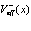 и
и 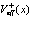 являются функциями, периодическими с периодом решетки кристалла.
являются функциями, периодическими с периодом решетки кристалла.
Выше мы никак не уточняли, насколько заполнены получившиеся электронная и позитронная зоны. Приведенный формализм может быть применен для случая полностью заполненной валентной зоны и соседней зоны проводимости с одним электроном или позитроном. Например, для функции избыточного электрона имеем
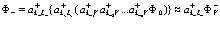 (78)
(78)
Функция избыточного позитрона в свою очередь имеет вид
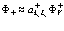 (79)
(79)
Здесь 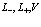 индексы, относящиеся к электронной и позитронной зонам проводимости и валентной зоны соответственно. Принимаем, что
индексы, относящиеся к электронной и позитронной зонам проводимости и валентной зоны соответственно. Принимаем, что 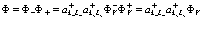 . Из этого уравнения следует вывод о том, что электронная дырка в твердом теле (или просто дырка) никоим образом не идентична позитрону, как реальной частице.
. Из этого уравнения следует вывод о том, что электронная дырка в твердом теле (или просто дырка) никоим образом не идентична позитрону, как реальной частице.
3. Электроны и позитроны в кристаллической решетк. Теорема Блоха
В выражениях (76) и (77) введем обозначения 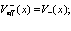
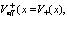
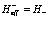 ,
, 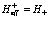 . Тогда
. Тогда 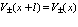 , где
, где  – один из векторов решетки, т.е. вектор, проведенный из одной точки решетки к следующей. Имеем
– один из векторов решетки, т.е. вектор, проведенный из одной точки решетки к следующей. Имеем
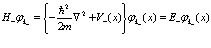
(80)
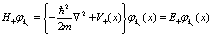
Далее
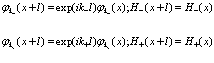 (81)
(81)
Отсюда
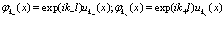 (82)
(82)
Подстановка (83) в (82) дает
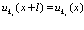 (83)
(83)
Соотношения (82) и (83) и представляют собой теорему Блоха.
Подставляя (82) в уравнения (80), получаем
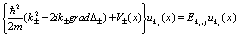 (84)
(84)
Энергию 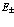 на краю зон можно разложить по
на краю зон можно разложить по 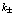 и при малых
и при малых 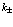 представить в виде
представить в виде
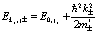 (85)
(85)
4. Метод эффективной массы
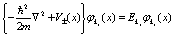 (86)
(86)
Здесь
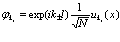
Так как
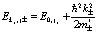 + (члены высокого порядка, которыми пренебрегаем), уравнение
+ (члены высокого порядка, которыми пренебрегаем), уравнение
Тогда уравнение типа (86)
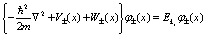
сводится к более простой проблеме

С учетом сдвига по энергии это уравнение переходит в
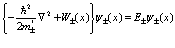 (87)
(87)
5. Функции Ванье: волновые пакеты из функций Блоха электронов и позитронов
Согласно [5], функции Ванье строятся из блоховских волн
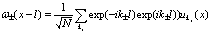 (88)
(88)
Здесь суммирование распространяется на все значения 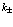 внутри данной энергетической зоны,
внутри данной энергетической зоны, 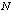 – число элементарных ячеек.
– число элементарных ячеек.
Функции Ванье обладают рядом важных свойств:
1. Функции Ванье описывают, например, локализацию позитрона в окрестности точки 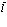 на протяжении примерно одной постоянной решетки.
на протяжении примерно одной постоянной решетки.
Докажем это, приняв, что 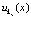 не зависит от
не зависит от 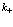 , то есть
, то есть 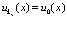 . В данном случае суммирование и (88) сразу же выполняется для всего кристалла (с точностью до фазового множителя)
. В данном случае суммирование и (88) сразу же выполняется для всего кристалла (с точностью до фазового множителя)
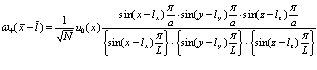
Здесь 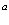 – постоянная решетки кристалла,
– постоянная решетки кристалла, 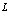 – линейный размер кристалла. В знаменателе синусы можно заменить на их аргументы. Тогда
– линейный размер кристалла. В знаменателе синусы можно заменить на их аргументы. Тогда
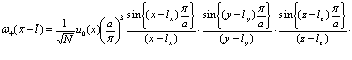 (89)
(89)
Из этого выражения легко видеть, что функция (89) действительно локализована в области пространства с размером 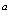 .
.
2. Важным свойством функций Ванье является их ортогональность, т.е. функции Ванье, локализованные в различных точках 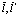 или принадлежащих разным значениям
или принадлежащих разным значениям 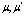 взаимно ортогональны.
взаимно ортогональны.
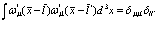 (90)
(90)
6. Электроны, позитроны, дырки в кристалле
6.1 Электронные дырки в кристалле
Формализм вторичного квантования позволяет очень элегантным образом ввести понятие дырки как квазичастицы и описать ее свойства. Исходя из заполненной валентной зоны, из которой удален электрон в состоянии 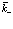 . Это незаполненное состояние ведет себя как частица, но уже с положительным зарядом. Этот процесс математически выглядит следующим образом
. Это незаполненное состояние ведет себя как частица, но уже с положительным зарядом. Этот процесс математически выглядит следующим образом
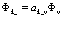 (91)
(91)
Здесь 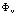 – волновая функция заполненной валентной зоны,
– волновая функция заполненной валентной зоны, 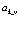 – оператор уничтожения, а
– оператор уничтожения, а 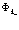 – волновая функция дырки. Вводим
– волновая функция дырки. Вводим
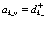 ,
, 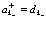 (92)
(92)
Причем
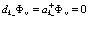 (93)
(93)
Таким образом состояние 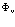 для оператора
для оператора 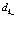 представляет вакуумное состояние. С учетом (31)-(33) имеем
представляет вакуумное состояние. С учетом (31)-(33) имеем
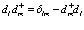 (94)
(94)
В свою очередь повторное применение этих перестановочных соотношений дает нам
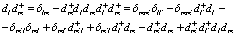 (95)
(95)
Подставляя (94) и (95) в электронную часть Гамильтониана, соответствующую электронам (индексы  и
и 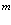 ), получаем последовательно: во-первых, у нас появляются члены, которые не зависят от операторов дырок, а именно символы Кронекера
), получаем последовательно: во-первых, у нас появляются члены, которые не зависят от операторов дырок, а именно символы Кронекера 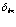 . Отсюда для энергии имеем некоторое постоянное значение
. Отсюда для энергии имеем некоторое постоянное значение
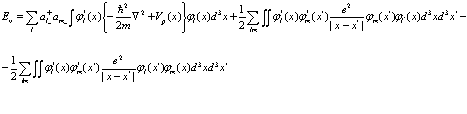 (96)
(96)
Здесь 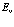 – энергия электронов валентной зоны кристаллов.
– энергия электронов валентной зоны кристаллов.
Во-вторых, рассмотрим члены в (60), содержащие пары операторов 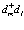 . Имеем
. Имеем
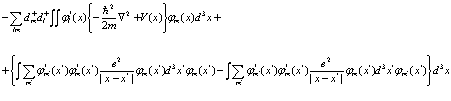 (97)
(97)
Здесь суммы по индексам 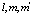 относятся ко всей валентной зоне. Можем записать (97) в виде
относятся ко всей валентной зоне. Можем записать (97) в виде
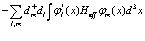 (98)
(98)
или иначе
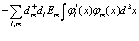 (99)
(99)
В виду ортогональности волновых функций выражение (97) приводится к виду
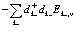 (100)
(100)
В третьих, как следует из (95), имеются еще операторы, содержащие производные четырех операторов дырок, соответствующие кулоновскому взаимодействию между дырками
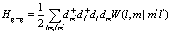 , (101)
, (101)
где
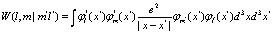 (102)
(102)
Теперь, объединяя (96), (100) и (101), получаем оператор Гамильтона дырок
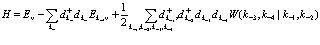 (103)
(103)
Опуская кулоновское взаимодействие между дырками и производя разложение энергии вблизи точки 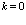 в ряд, получаем
в ряд, получаем
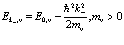 (104)
(104)
Таким образом, оператор Гамильтона для дырок имеет вид
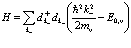 (105)
(105)
Отсюда следует, что дырки ведут себя как частицы с положительной эффективной массой 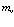 .
.
6.2 Взаимодействие между электронами, дырками и позитронами
Рассмотрим полупроводниковый кристалл, в основном состоянии которого валентная зона полностью занята электронами, а зона проводимости пустая. Исследуем вопрос о том, какие эффективные взаимодействия следует учитывать, если удалить некоторые электроны из валентной зоны, то есть создать в ней дырки, в зону проводимости. Причем не обязательно число дырок равно числу электронов в зоне проводимости. Их число при комнатной температуре может быть значительно больше за счет ионизации мелких примесных центров. Позитрон вводится в кристалл, например, из 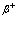 – радиоактивного источника – изотопа
– радиоактивного источника – изотопа 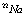 и образует в кристалле позитронную зону проводимости. Пусть такого рода систему описывает уравнение Шредингера
и образует в кристалле позитронную зону проводимости. Пусть такого рода систему описывает уравнение Шредингера
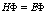 (106)
(106)
с оператором Гамильтона
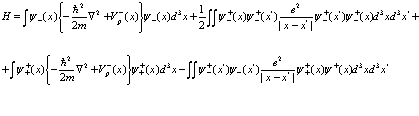 (107)
(107)
Так как мы хотим рассмотреть состояния в валентной зоне и электроны и позитрон в зонах проводимости в явном виде, разложим операторы поля по собственным функциям валентной зоны и зон проводимости
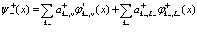 (108)
(108)
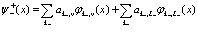 (109)
(109)
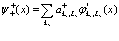 (110)
(110)
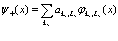 (111)
(111)
При этом предполагаем, что волновые функции 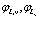 определяются с помощью эффективных Гамильтонианов
определяются с помощью эффективных Гамильтонианов
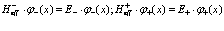 , (112)
, (112)
где
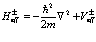 (113)
(113)
Условия ортонормированности имеют вид
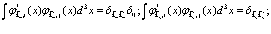 (114)
(114)
В соответствии со слагаемыми, входящими в (107), разложим оператор Гамильтона на отдельные части
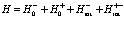 (115)
(115)
Подставляя разложения (108)-(111) в соответствующие разложения, получаем выражения для 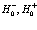
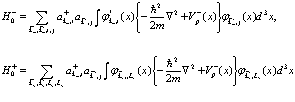 (116)
(116)
Заметим, что ввиду трансляционной симметрии задачи, двойное суммирование по 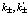 переходит в однократное. Третье слагаемое, стоящее в (115), после подстановки разложений (108)-(111) принимает вид
переходит в однократное. Третье слагаемое, стоящее в (115), после подстановки разложений (108)-(111) принимает вид
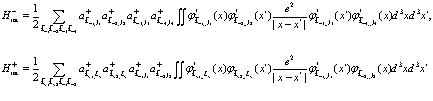 (117)
(117)
В дальнейшем вместо электронных операторов валентной зоны вводим операторы дырок
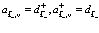 (118)
(118)
Далее несколько упростим наши обозначения, а именно, опустим у операторов, относящихся к электронам проводимости и позитрону, индексы 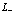 и
и 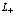 :
:
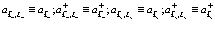
Сделаем необходимое допущение о сохранении количества дырок, электронов и позитронов, то есть рассмотрим стационарные состояния системы. Акты аннигиляции позитронов и дырок на начальном этапе не учитываем. К тому же пренебрегаем виртуальными переходами, обусловленными перекрыванием волновых функций валентной зоны и зоны проводимости (так называемые поляризационные эффекты). Дальнейший формализм расчета состоит в том, что согласно (118), вводятся операторы дырок, затем оператор Гамильтона преобразуется таким образом, чтобы операторы уничтожения стояли справа. Проведем в 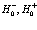 следующие опрощения и преобразования:
следующие опрощения и преобразования:
для 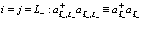 (119)
(119)
для 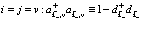 (120)
(120)
для 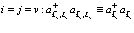 (121)
(121)
В 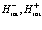 необходимо учесть все возможные комбинации индексов, таких как:
необходимо учесть все возможные комбинации индексов, таких как:
1. Все индексы принадлежат электронной зоне проводимости
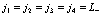 (122)
(122)
2. Все индексы принадлежат валентной зоне
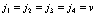 (123)
(123)
3. Все индексы принадлежат валентной зоне и два – зоне проводимости, то есть
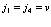 ;
; 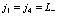 ;
;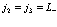 ;
;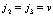 , (124)
, (124)
а также следующие комбинации индексов
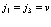 ;
; 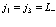 ;
;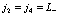 ;
;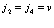 , (125)
, (125)
которые дают равным образом одинаковые вклады. Введем краткое обозначение матричного элемента, описывающего кулоновское взаимодействие
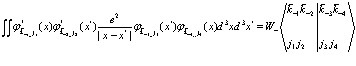 (126)
(126)
Верхний ряд индексов в 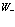 и
и  относятся к векторам
относятся к векторам 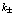 , а нижний ряд
, а нижний ряд 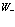 к индексам зоны проводимости или валентной зоны. Индексы
к индексам зоны проводимости или валентной зоны. Индексы 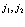 принимают естественно значения
принимают естественно значения 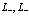 , либо
, либо 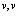 .
.
Рассмотрим матричный элемент кулоновского взаимодействия для позитрона
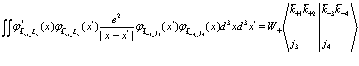 (127)
(127)
Опять-таки индексы 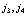 принимают естественно значения
принимают естественно значения 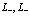 , либо
, либо 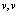 .
.
Согласно комбинации индексов имеются разные вклады в операторы взаимодействия 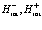 , а именно: взаимодействия в зоне проводимости и взаимодействия между зоной проводимости и валентной зоной
, а именно: взаимодействия в зоне проводимости и взаимодействия между зоной проводимости и валентной зоной
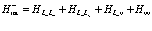 (128)
(128)
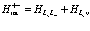 (129)
(129)
Итак, в соответствии с (128) и (129) получаем следующие вклады:
1. Взаимодействие между электронами проводимости
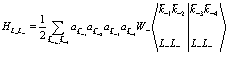 (130)
(130)
2. Взаимодействие между электронами проводимости и позитроном
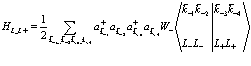 (131)
(131)
3. Взаимодействие между дырками в валентной зоне
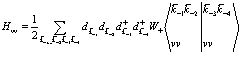 (132)
(132)
Перенесем в данном выражении операторы уничтожения направо и проведем соответствующие преобразования. Тогда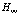 можно представить в виде
можно представить в виде
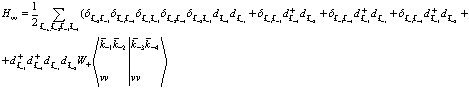 (133)
(133)
Рассмотрим отдельные члены в выражении (133) от A до G, причем для этого необходимо вычислить множитель W в (133). Член А дает кулоновское взаимодействие в заполненной валентной зоне и экспериментально не наблюдаем. Член В характеризует кулоновское обменное взаимодействие в заполненной валентной зоне, в то время как член С дает взаимодействие дырок с валентными электронами, а Д представляет соответствующее кулоновское обменное взаимодействие. Последние члены совпадают с предыдущими: Е=Д и F=C. Члены С и Д, как видели ранее, участвуют в определении волновых функций зоны с помощью метода самосогласованного поля, т.е. в данном случае они для нас не интересны, за исключением члена G. Тогда имеем
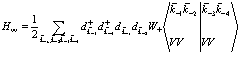 (134)
(134)
4. Взаимодействие между электронами проводимости и дырками
Согласно табличкам 128) и (129) в них присутствуют два разнородных члена. Исследуем выражение,
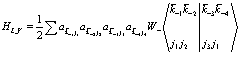 , (135)
, (135)
где на индексы 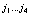 наложены ограничения (128) и (129). Рассмотрим вклады по следующей схеме
наложены ограничения (128) и (129). Рассмотрим вклады по следующей схеме
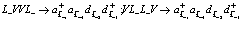 (136)
(136)
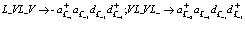 (137)
(137)
Можно легко показать, что вклады в (135) от комбинаций (136) и (137) идентичны внутри себя. Для этого надо изменить в сумме (135) следующим образом: 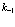 заменим на
заменим на 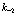 ,
, 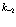 на
на 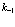 ,
, 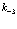 на
на 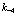 и
и 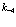 на
на 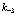 . Тем самым вторая строка в (135) переходит в новый матричный элемент
. Тем самым вторая строка в (135) переходит в новый матричный элемент
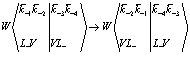 , (138)
, (138)
причем в явном выражении для матричного элемента следует поменять координаты 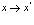 .
.
Таким образом, матричные элементы в (138) равны друг другу. То же самое относится и к (137). Таким образом для дальнейшего, если ограничиться первыми членами в (136) и (137), а оставшиеся комбинации учтем просто введением в сумме (135) множителя 2. Выражение для взаимодействия согласно первой строке (136) можно преобразовать с помощью перестановочных соотношений для дырок. При этом получаем
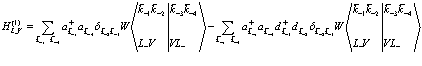 , (139)
, (139)
Первая сумма в (139) описывает взаимодействие электронов в зоне проводимости с заполненной валентной зоной. Это видно, если несколько преобразовать это выражение, используя стоящие в них символы Кронекера. Тогда для первой части выражения (139) получаем
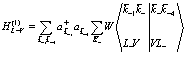 , (140)
, (140)
Для того, чтобы сделать это выражение физически ясным, воспользуемся видом 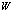 , представленным в (126). После чего получаем
, представленным в (126). После чего получаем
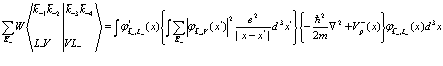 , (141)
, (141)
Как раз это выражение в (135) и определяет собой энергию взаимодействия электронов проводимости с заполненной валентной зоной. Второе выражение в (136), относящееся к (135), описывает уничтожение и последующее рождение дырки и одновременно тем самым уничтожение и последующее рождение электрона и одновременно тем самым уничтожение и последующее рождение электрона. Это выражение таким образом описывает рассеяние электрона на дырке, которое обусловлено кулоновским взаимодействием. Это рассеяние в рамках нашего формализма заключено в выражении 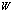 . Аналогичным образом опишем взаимодействие в (135), которое обусловлено (137). Отсюда сразу получаем
. Аналогичным образом опишем взаимодействие в (135), которое обусловлено (137). Отсюда сразу получаем
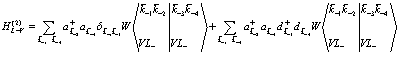 , (142)
, (142)
Первую сумму в этом выражении можно интерпретировать как обменное взаимодействие электронов в зоне проводимости с заполненной валентной зоной, а вторя сумма (наиболее важная) описывает кулоновское взаимодействие (обменное) между электронами в зоне проводимости и дыркой. То, что здесь действительно речь идет об обменном взаимодействии, становится ясным, если исследовать явное выражение для 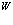 . При этом следует, что для равных значений
. При этом следует, что для равных значений 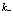 в зоне проводимости, т.е. для
в зоне проводимости, т.е. для 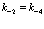 , появляется смешанная зарядовая плотность.
, появляется смешанная зарядовая плотность.
5. Взаимодействие позитрона с электронами проводимости и электронами полностью заполненной валентной зоны
Сразу же можем записать
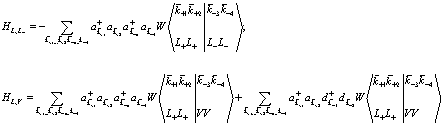 (143)
(143)
В выражении (143) первый член соответствует кулоновскому взаимодействию позитрона в зоне проводимости с электронами полностью заполненной валентной зоны, а второй член отвечает кулоновскому взаимодействию позитрона с дырками в валентной зоне.
Для полной ясности объединим полученные выше результаты в общий оператор Гамильтона для электронов, дырок и позитрона в кристалле
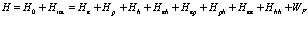 (144)
(144)
Рассмотрим вклады, соответствующие (144)
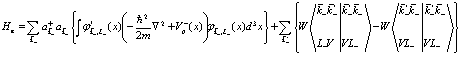 , (145)
, (145)
Этот член описывает энергию электронов в зоне проводимости (однако без учета взаимодействия электронов с электронами, дырками и позитроном). Это выражение обсуждалось уже ранее.
Для позитрона имеем
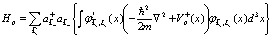 (146)
(146)
Этот член описывает энергию позитрона в позитронной зоне проводимости. Для дырок получаем
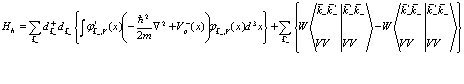 , (147)
, (147)
И это выражение мы уже рассматривали ранее.
Взаимодействие между электронами и дырками описывается выражением
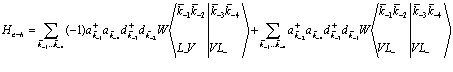 , (148)
, (148)
В свою очередь взаимодействие между электронами и позитроном определяется выражением
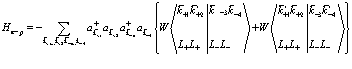 (149)
(149)
Взаимодействие между позитроном и дырками описывается выражением
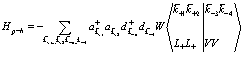 (150)
(150)
Три последних члена в (144) интерпретируются следующим образом.
Во-первых, это электрон-электронное взаимодействие в зоне проводимости
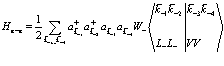 (151)
(151)
Во-вторых, это взаимодействие между дырками в валентной зоне
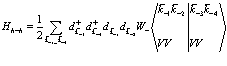 (152)
(152)
В- третьих, это постоянный член, который не содержит никаких операторов
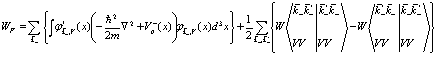 , (153)
, (153)
который описывает энергию валентной зоны.
Отметим, что записанные выше выражения (145), (146) и (147) представляют средние значения энергий электронов, позитрона и дырок: 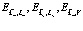 . Можно принять для реальных условий экспериментов, что электроны, позитрон и дырки находятся вблизи краев зон. Поэтому используем разложения
. Можно принять для реальных условий экспериментов, что электроны, позитрон и дырки находятся вблизи краев зон. Поэтому используем разложения
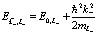 , (154)
, (154)
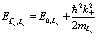 , (155)
, (155)
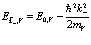 , (156)
, (156)
В рамках рассмотренной задачи решим проблему экситона, атома позитрония (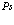 ) и позитрон-экситонного комплекса.
) и позитрон-экситонного комплекса.
7. Экситоны, атом 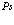 и позитрон-экситонные комплексы
и позитрон-экситонные комплексы
Рассмотрим вначале проблему позитрон-экситонного комплекса в кристалле, т.е. систему, сосоящую из взаимодействующих между собой электрона, позитрона и дырки. Будем исходить из оператора Гамильтона системы электронов, позитрона и дырок в обозначениях Хакена [5]
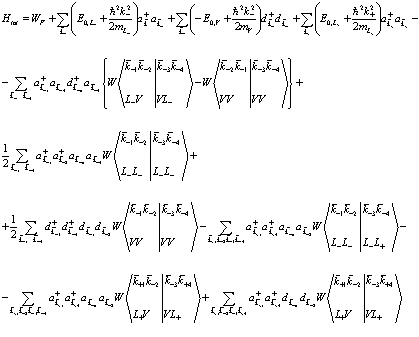 (157)
(157)
В этом выражении первый член представляет собой энергию полностью заполненной зоны, второй член представляет кинетическую энергию электрона (индекс 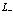 ), третий член – кинетическую энергию дырок в валентной зоне (индекс
), третий член – кинетическую энергию дырок в валентной зоне (индекс 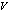 ), четвертый – кинетическую энергию позитрона в позитронной зоне проводимости (индекс
), четвертый – кинетическую энергию позитрона в позитронной зоне проводимости (индекс 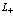 ), пятый член описывает взаимодействие между дырками и электронами, шестой член – взаимодействие между электронами в зоне проводимости, седьмой член – взаимодействие между дыркам в валентной зоне, восьмой член описывает взаимодействие электронов проводимости (индекс
), пятый член описывает взаимодействие между дырками и электронами, шестой член – взаимодействие между электронами в зоне проводимости, седьмой член – взаимодействие между дыркам в валентной зоне, восьмой член описывает взаимодействие электронов проводимости (индекс 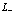 ) и позитроном в позитронной зоне проводимости (индекс
) и позитроном в позитронной зоне проводимости (индекс 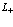 ) и, наконец, девятый представляет энергию взаимодействия позитрона позитронной зоны проводимости (индекс
) и, наконец, девятый представляет энергию взаимодействия позитрона позитронной зоны проводимости (индекс 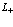 ) и дырками в валентной зоне (индекс
) и дырками в валентной зоне (индекс 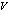 ).
).
Следовательно задача позитрон-экситонного комплекса заключается в решении уравнения Шредингера
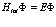 (158)
(158)
Приведем это решение в явном виде для случая одного электрона, позитрона и дырки. Волновые функции электрона в состоянии 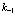 , позитрона в состоянии
, позитрона в состоянии 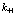 и дырки в состоянии
и дырки в состоянии 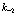 можно получить из состояния, описывающего полностью заполненную валентную зону, последовательным действием операторов рождения
можно получить из состояния, описывающего полностью заполненную валентную зону, последовательным действием операторов рождения 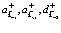 на функцию заполненной зоны
на функцию заполненной зоны 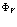
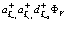 (159)
(159)
Следует отметить, что в общем случае  .
.
Из выражения (159) следует, что электрон, дырка и позитрон, пролетая друг относительно друга, испытывают естественно взаимное рассеяние, в результате чего попадают во все возможные различные конечные состояния 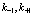 . Поэтому следует образовать сумму по всем состояниям
. Поэтому следует образовать сумму по всем состояниям 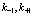 электрона, позитрона и дырки. Исходя из этого соображения, подход к системе позитрон-экситонного комплекса будет основан на волновой функции
электрона, позитрона и дырки. Исходя из этого соображения, подход к системе позитрон-экситонного комплекса будет основан на волновой функции
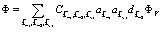 (160)
(160)
Теперь Гамильтониан (157) упрощается, т.к. отсутствуют члены, соответствующие взаимодействию электронов в зоне проводимости и дырок в валентной зоне.
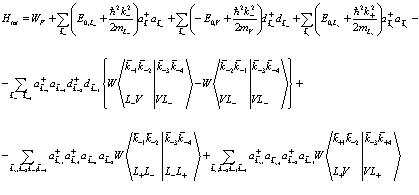 (161)
(161)
Оператор (161) разложим, как обычно, на две части: кинетическую энергию электрона, позитрона и дырки и взаимодействия между ними (при этом, чтобы опустить член 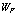 в (161) сдвинем соответствующим образом энергию
в (161) сдвинем соответствующим образом энергию 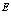 ).
).
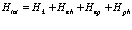 (162)
(162)
Учитывая явный вид 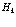 в (161) и волновой функции (160), получаем
в (161) и волновой функции (160), получаем
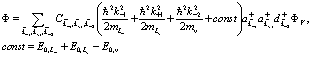 (163)
(163)
В свою очередь запишем правую часть выражения (158) в явном виде
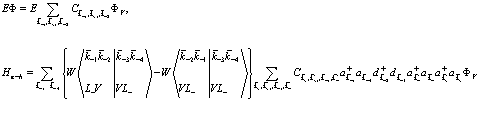 (164)
(164)
С помощью фермиевских перестановочных соотношений можем значительно упростить выражение (164), перетащив все операторы уничтожения направо и учтя также, что действие на 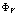 электронных, позитронных и дырочных операторов дает нуль. Поменяв индексы 3,2,4 местами (2 на 4, 3 на 2, и 4 на 3 – во втором члене (163), можем записать выражение (164) в виде
электронных, позитронных и дырочных операторов дает нуль. Поменяв индексы 3,2,4 местами (2 на 4, 3 на 2, и 4 на 3 – во втором члене (163), можем записать выражение (164) в виде
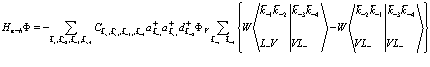 (165)
(165)
Далее
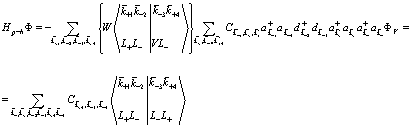 (166)
(166)
И, наконец
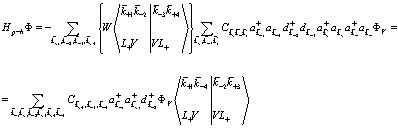 (167)
(167)
Можно видеть, что в выражениях (164), (165)-(167) появились линейные комбинации волновых функций, которые имеют вид (159). Причем известно, что функции вида (159) взаимно ортогональны для различных векторов 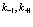 . Тогда уравнение (158), в левой части которого стоят выражения (163), (165)-(167) может быть удовлетворено, если равны между собой коэффициенты функций (160). Сравнивая коэффициенты, получаем систему уравнений для коэффициентов
. Тогда уравнение (158), в левой части которого стоят выражения (163), (165)-(167) может быть удовлетворено, если равны между собой коэффициенты функций (160). Сравнивая коэффициенты, получаем систему уравнений для коэффициентов 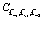
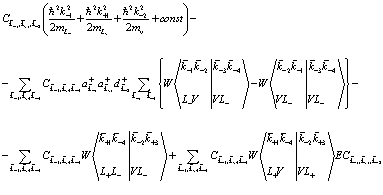 (168)
(168)
Можно показать, что система уравнений (168) эквивалентна полностью обычному трехчастичному уравнению Шредингера, причем между электроном, позитроном и дыркой существует кулоновское взаимодействие. Упростим для этого матричные элементы, входящие в (168)
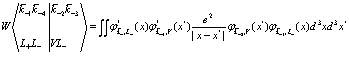 (169)
(169)
Используем в (169) для волновых функций в зонах явный вид блоховской волны
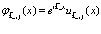 (170)
(170)
Разложим функции 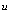 , зависящие от
, зависящие от 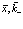 в ряд Тейлора по
в ряд Тейлора по 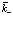 (то есть для малых
(то есть для малых 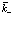 ). Имеем в этом случае
). Имеем в этом случае
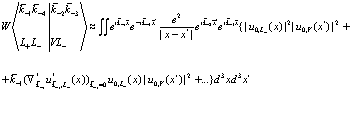 (171)
(171)
Далее делаем следующие предположения: во-первых, играющая заметную роль значения 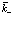 настолько малы, что из всего ряда Тейлора сохраним лишь первый член. Таким образом в фигурных скобках выражения (171) оставляем лишь член
настолько малы, что из всего ряда Тейлора сохраним лишь первый член. Таким образом в фигурных скобках выражения (171) оставляем лишь член 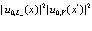 . Эта функция периодична с периодом решетки, однако внутри элементарной ячейки она может быстро осциллировать. Так мы приняли, что важны только малые значения
. Эта функция периодична с периодом решетки, однако внутри элементарной ячейки она может быстро осциллировать. Так мы приняли, что важны только малые значения 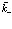 (то есть
(то есть 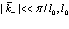 – постоянная решетки), то экспоненциальные функции в (171) можно вычислить, усреднив его по отдельным элементарным ячейкам. Заметим, что блоховские функции должны быть нормированы в объеме
– постоянная решетки), то экспоненциальные функции в (171) можно вычислить, усреднив его по отдельным элементарным ячейкам. Заметим, что блоховские функции должны быть нормированы в объеме 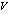 на единицу. Таким образом, при усреднении появляется множитель
на единицу. Таким образом, при усреднении появляется множитель 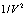 . После этого выражение (171) запишем в виде
. После этого выражение (171) запишем в виде
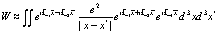 (172)
(172)
Вторым выражением во втором члене формулы (168) пренебрегаем, который описывает обменной взаимодействие.
Рассмотри далее матричный элемент 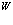 в третьем члене выражения (168)
в третьем члене выражения (168)
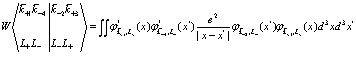 , (173)
, (173)
где
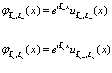 (174)
(174)
После преобразований, описанных выше, для выражения (169) получаем
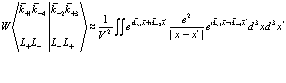 (175)
(175)
Матричный элемент, входящий в четвертый член выражения (168), равен
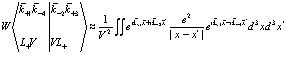 (176)
(176)
Можно утверждать, что система уравнений (168) с упрощениями (172), (175) и (176) эквивалентна следующему трехчастичному уравнению
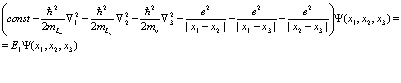 (177)
(177)
Для доказательства этого утверждения следует представить волновую функцию 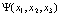 в виде
в виде
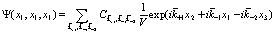 (178)
(178)
Умножим (168) на выражение
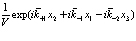 (179)
(179)
и просуммируем по 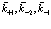 .
.
Вначале рассмотрим члены, относящиеся к кинетической энергии
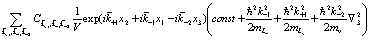 (180)
(180)
Так как 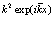 можно представить в виде
можно представить в виде
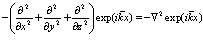 , (181)
, (181)
то (180) переходит в следующее выражение
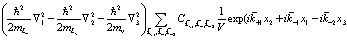 (182)
(182)
Согласно (178) это выражение эквивалентно выражению
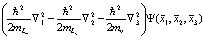 (183)
(183)
Часть, описывающая электрон-дырочное взаимодействие (168) с использованием (172) после умножения на (179) принимает вид
 (184)
(184)
Теперь соберем вместе все экспоненциальные функции, содержащие 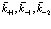 , и воспользуемся соотношением
, и воспользуемся соотношением
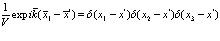 (185)
(185)
Ввиду появления 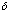 - функций интегрирование в (184) пропадает и выражение (184) переходит (при
- функций интегрирование в (184) пропадает и выражение (184) переходит (при 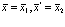 ) в выражение
) в выражение
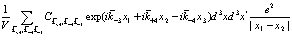 (186)
(186)
Но это выражение тождественно совпадает с выражением
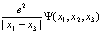 (187)
(187)
Аналогично получаем выражения, входящие в уравнение (177)
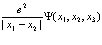 (188)
(188)
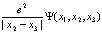 (189)
(189)
Заметим далее, что в поляризуемой среде закон Кулона модифицируется с учетом диэлектрической проницаемости. Следовательно, в выражении (177) в феноменологическом приближении надо заменить 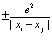 на
на 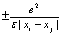 . То обстоятельство, что в нашем рассмотрении
. То обстоятельство, что в нашем рассмотрении 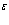 не появилось, связано со значительным упрощением Гамильтониана, где мы пренебрегли виртуальными переходами.
не появилось, связано со значительным упрощением Гамильтониана, где мы пренебрегли виртуальными переходами.
Тогда трехчастичное уравнение Шредингера с учетом вышесказанного запишется в виде
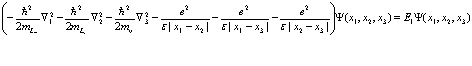 (190)
(190)
Уравнение Шредингера представляет собой описание позитрон экситонного комплекса Ванье большого радиуса. Такого рода система является аналогом систем (комплексов) Уилера [9,10] (ионы позитрония). Он был открыт в блестящих экспериментах Миллса [11] относительно недавно. Обзоры теоретических расчетов такого рода систем был дан ранее в работах [12-20]. Сродство к позитрону (электрону) для таких систем составляет величины не менее 0,1 эВ, время жизни относительно двухквантовой аннигиляции – 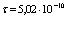 с.
с.
Заметим, что уравнение (190) для атома 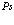 большого радиуса в кристалле принимает вид
большого радиуса в кристалле принимает вид
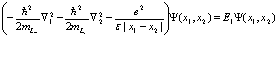 (191)
(191)
Его решение подробно анализируется в монографиях по квантовой электродинамике (см., например, [8]) и в ряде конкретных работ [12-20]. Наряду с приближением (191) представляет большой интерес проблема атома 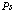 малого радиуса в кристалле, которую рассмотрим ниже.
малого радиуса в кристалле, которую рассмотрим ниже.
8. Модель Френкеля атома 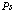 малого радиуса в кристалле
малого радиуса в кристалле
В разделе 7 постулировалось утверждение о том, что расстояние между электроном, позитроном, дыркой велики, так что вполне разумным было разложение операторов поля 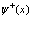 и
и 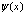 по блоховским функциям (волнам). В данном разделе рассмотрим противоположный случай, когда позитрон и электрон находятся на одном и том же атоме. При этом разложение будем проводить ьне блоховским волнам, а по атомным функциям, или по функциям Ванье, свойства которых обсуждались нами ранее. Так мы имеем две зоны – позитронную и электронную зону проводимости, то введем следующие функции Ванье
по блоховским функциям (волнам). В данном разделе рассмотрим противоположный случай, когда позитрон и электрон находятся на одном и том же атоме. При этом разложение будем проводить ьне блоховским волнам, а по атомным функциям, или по функциям Ванье, свойства которых обсуждались нами ранее. Так мы имеем две зоны – позитронную и электронную зону проводимости, то введем следующие функции Ванье
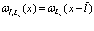 (позитронная зона проводимости), (192)
(позитронная зона проводимости), (192)
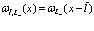 (электронная зона проводимости), (193)
(электронная зона проводимости), (193)
где 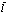 – радиус-вектор точки локализации частиц.
– радиус-вектор точки локализации частиц.
Разложение электронных и позитронных полевых операторов 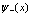 ,
, 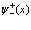 и
и 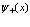 ,
, 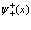 по функциям Ванье записывется в виде
по функциям Ванье записывется в виде
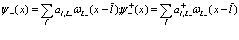 (194)
(194)
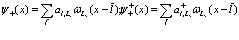 (195)
(195)
Операторы 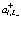 и
и 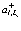 рождают электрон и позитрон в электронной и позитронной зонах проводимости, а операторы
рождают электрон и позитрон в электронной и позитронной зонах проводимости, а операторы 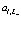 и
и 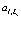 уничтожают их в тех же зонах соответственно.
уничтожают их в тех же зонах соответственно.
Так как функции Ванье представляют собой ортогональную систему функций, то согласно выше изложенному 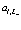 и
и 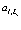 удовлетворяют перестановочным соотношениям
удовлетворяют перестановочным соотношениям
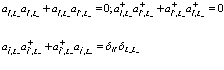 , (196)
, (196)
и
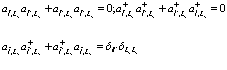 (197)
(197)
Теперь следует выразить оператор Гамильтона 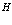 , как уже делали ранее в п. 7, через операторы рождения и уничтожения
, как уже делали ранее в п. 7, через операторы рождения и уничтожения 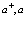 . Разложим
. Разложим 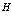 на два члена
на два члена 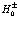 – операторы кинетической энергии электрона и позитрона в поле заданного атома и
– операторы кинетической энергии электрона и позитрона в поле заданного атома и 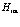 – кулоновское взаимодействие между электроном и позитроном. Итак, получаем
– кулоновское взаимодействие между электроном и позитроном. Итак, получаем
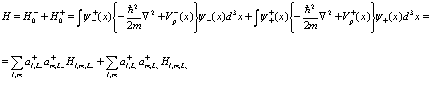 (198)
(198)
Здесь использованы сокращенные обозначения
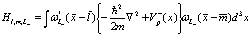 (199)
(199)
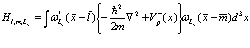 (200)
(200)
Если сделать предположение о том, что операторы в фигурных скобках (198) не приводят к переходам между электронной и позитронной зонам, то, преобразовывая соответствующим образом выражение
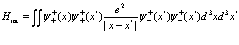 , (201)
, (201)
получаем
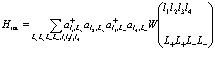 , (202)
, (202)
где
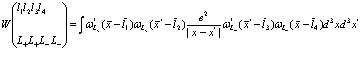 , (203)
, (203)
Сделаем упрощения, согласно которым можно пренебречь перекрыванием волновых функций. В этом случае примем, что 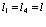 , а
, а 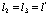 . При этом уравнение (202) может быть записано в виде
. При этом уравнение (202) может быть записано в виде
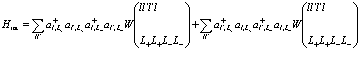 , (204)
, (204)
где
 , (205)
, (205)
Таким образом, полный Гамильтониан френкелевской модели атома 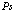 имеет вид
имеет вид
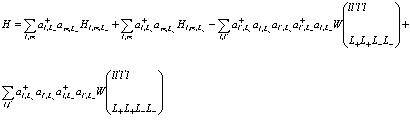 (206)
(206)
Каждый член Гамильтониана имеет очень наглядный физический смысл: в первой сумме с членами 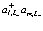 один электрон в точке
один электрон в точке 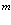 электронной зоны проводимости уничтожается, а в точке
электронной зоны проводимости уничтожается, а в точке  вновь рождается; во второй сумме с членами
вновь рождается; во второй сумме с членами 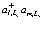 один позитрон в точке
один позитрон в точке 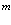 позитронной зоны проводимости уничтожается, а в точке
позитронной зоны проводимости уничтожается, а в точке  вновь рождается. Эти части Гамильтониана, следовательно, описывают движение электрона (позитрона) и дырки.
вновь рождается. Эти части Гамильтониана, следовательно, описывают движение электрона (позитрона) и дырки.
Третий член Гамильтониана (206) не описывает никакого переноса, позитрон остается в точке 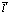 , а электрон в точке –
, а электрон в точке – 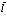 . Этот член описывает кулоновское взаимодействие электрона и позитрона в атоме
. Этот член описывает кулоновское взаимодействие электрона и позитрона в атоме 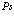 . Четвертый член с членами
. Четвертый член с членами 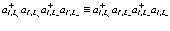 описывает уничтожение электронно-дырочной пары в точке
описывает уничтожение электронно-дырочной пары в точке 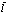 и последующее рождение в точке
и последующее рождение в точке 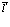 или наоборот, т.е. описывает совместный перенос позитрона и электрона.
или наоборот, т.е. описывает совместный перенос позитрона и электрона.
Введем теперь явный вид функции состояния полностью заполненной валентной зоны 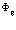 . В точке
. В точке 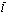 рождается одновременно электрон и позитрон. В силу трансляционной симметрии нашей задачи должны провести суммирование по всем точкам локализации
рождается одновременно электрон и позитрон. В силу трансляционной симметрии нашей задачи должны провести суммирование по всем точкам локализации 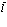 с множителем
с множителем 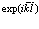 . Волновая функции таким образом запишется в виде
. Волновая функции таким образом запишется в виде
 (207)
(207)
Здесь
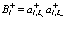 (208)
(208)
есть оператор рождения локализованного в точке 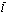 атома
атома 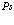 . Соответствующий оператор уничтожения атома
. Соответствующий оператор уничтожения атома 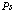 есть
есть
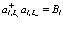 (209)
(209)
Выразим полный Гамильтониан (206) через операторы 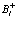 и
и 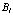 . Стоящие в последнем члене операторы выражаются через оператор
. Стоящие в последнем члене операторы выражаются через оператор 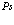 следующим образом
следующим образом
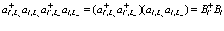 (210)
(210)
Таким образом, выражение, описывающее уничтожение 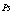 в точке
в точке 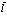 и рождение его в точке
и рождение его в точке 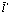 описывается выражением
описывается выражением
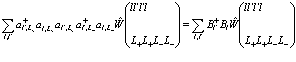 (211)
(211)
Теперь рассмотрим, какой вклад дает третий член в (206). Рассмотрим действие стоящих в нем операторов на локализованное позитрониевое состояние. Получаем
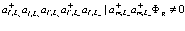 , (212)
, (212)
т.е. при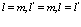 .
.
При использовании волновой функции (207) из третьего слагаемого (206) следует сохранить лишь те члены, для которых индексы  и
и 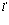 равны
равны
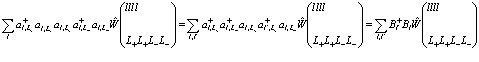 (213)
(213)
Это выражение приводит лишь к изменению энергии локализованного состояния 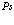 и не может приводить к переходам между различными точками в кристалле. Теперь рассмотрим два первых члена в (206). Рассмотрим действие типичных операторов из первой суммы на локализованной состояние
и не может приводить к переходам между различными точками в кристалле. Теперь рассмотрим два первых члена в (206). Рассмотрим действие типичных операторов из первой суммы на локализованной состояние
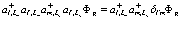 (214)
(214)
Учтем лишь члены с 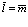 , так как в противном случае позитрон и электрон далеко уходят друг от друга. Следовательно полагаем
, так как в противном случае позитрон и электрон далеко уходят друг от друга. Следовательно полагаем
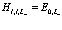 , (215)
, (215)
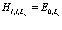 , (216)
, (216)
Тогда
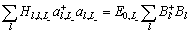 (217)
(217)
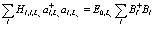 (218)
(218)
Таким образом, выражение (206) может быть записано в виде
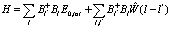 (219)
(219)
Здесь введены обозначения
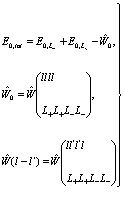 (220)
(220)
Покажем теперь, что функция состояния (207) является решением соответствующего Гамильтониана (219) уравнения Шредингера, и определим собственные значения энергии этого уравнения. Так как
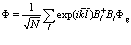
Тогда
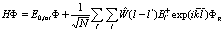 (221)
(221)
Второй член в (221) преобразуем так
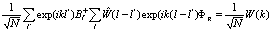 (222)
(222)
Таким образом
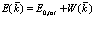 (223)
(223)
Если разложить 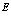 по волновому вектору
по волновому вектору 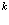 , то, как обычно получаем
, то, как обычно получаем
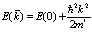 (224)
(224)
Таким образом мы рассмотрели состояния электронов, дырок, экситонов и атома 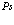 малого и большого радиуса. На основании данного формализма возможно рассмотрение расчетных методов аннигиляционных характеристик этих состояний в различных средах (например, в ионных кристаллах и гидридах щелочных металлов).
малого и большого радиуса. На основании данного формализма возможно рассмотрение расчетных методов аннигиляционных характеристик этих состояний в различных средах (например, в ионных кристаллах и гидридах щелочных металлов).
Список литературы
- PHYSICS WITH MANY POSITRONS”. INTERNATIONAL SCHOOL OF PHYSICS ENRICO FERMI. 7-17 July – VARENNA –ITALY. Directors: A. P. Mills, A. Dupasquier. 2009.
- V.A.Fock // Zs. f. Phys. 1932. Vol.75. P.622.
- Чжан Ли // Диссертация. Л.: ЛГУ, 1956.
- Г. Хакен. Квантовополевая теория твердого тела. М.: ГИФМЛ, 1980.
- Прокопьев Е.П. Введение в теорию позитронных процессов в полупроводниках и ионных кристаллах. М., 1979. 384 с. – Деп. в ЦНИИ “Электроника”. Р-2837. МРС ВИМИ “Техника, технология, экономика”. №27. 1980. Сер.”ЭР”
-
Прокопьев Е.П. Позитроны и позитроний в кристаллах. М., 1982. 138 с. – Деп. в ЦНИИ “Электроника”. Р-3475. МРС ВИМИ “Техника, технология, экономика”. №8. 1983. Сер.”ЭР”.
-
Прокопьев Е.П. Исследования позитронных процессов в кристаллах. М., 1982. 60 с. – Деп. в ЦНИИ”Электроника”. Р-3556. МРС ВИМИ “Техника, технология, экономика”. 1983. Сер.”ЭР”.
- Берестецкий В.Б. Квантовая электродинамика. М.: Наука, 1969.
-
J.Wheeler // Ann. N. Y. Acad. Sci, 1946. Vol,48. P.219.
-
Прокопьев Е.П. Комплексы Уилера в полупроводниках. – М., 1979. – 12 с. – Деп. в ЦНИИ “Электроника”. Р-2757. МРС ВИМИ “Техника, технология, экономика”. – № 28. – 1979. – Сер. “ЭР”.
-
Mills A.P. Observation of the Positronium Negative Ion. Phys. Rev. Letters. 1981. Vol. 46, Number 11. P.717-720.
-
Прокопьев Е.П., Кузнецов Ю.Н., Хашимов Ф.Р. Основы позитроники полупроводников. М.,1976. 343 с. – Деп. в ЦНИИ “Электроника”. Р-2073. РИ.77.06.3412.
-
Арефьев К.П., Воробьев С.А., Прокопьев Е.П. Позитроника в радиационном материаловедении ионных структур и полупроводников. М.: Энергоатомиздат, 1983. 88 с.
-
Е.П.Прокопьев, С.П.Тимошенков, В.И.Графутин, Г.Г.Мясищева, Ю.В.Фунтиков. Позитроника ионных кристаллов, полупроводников и металлов. М.: Ред.-изд. отдел МИЭТ (ТУ), 1999. 176 с.
-
В.И.Гольданский. Физическая химия позитронов и позитрония. М.: Наука, 1968.
-
Прокопьев Е.П. Об аномальных свойствах атома позитрония (Ps) в ионных кристаллах и полупроводниках // Физика твердого тела. 1977. Т.19. Вып.2. С.472-475.
-
Прокопьев Е.П. Позитроний и его свойства в полупроводниках и щелочно-галоидных кристаллах // Химия высоких энергий. 1978. Т.12. Вып.2. С.172-174.
-
Кузнецов Ю.Н., Прокопьев Е.П., Варисов А.З. Основы теории позитронных состояний в ионных кристаллах. – М., 1978. – 292 с. – Деп. в ЦНИИ “Электроника”, Р-2382. Сб. ВИМИ “Военная техника и экономика”. Сер. общетехническая. – № 14. – 1978.
-
Варисов А.З., Арефьев К.П., Воробьев А.А., Кузнецов Ю.Н., Прокопьев Е.П. Позитроны в конденсированных средах. – М., 1977. – 489 с. – Деп. в ЦНИИ “Электроника”. Р-2317. Сб. ВИМИ “Военная техника и экономика”. Сер. общетехническая. – № 9. – 1978.
-
Прокопьев Е.П. Исследования в области физики медленных позитронов. Позитронная аннигиляция – новый метод изучения строения вещества. – М., 1986. – 86 с. – Деп. в ЦНИИ “Электроника”. Р-4367. Сб. реф. НИОКР, обзоров, переводов и деп. рукописей. Сер. “ИМ”. – №12. – 1987.
УДК 539.21:539.189.2
Позитроны, позитроний, позитронные и позитрониевые комплексы в кристалле. ОБЗОР
II. Особенности их свойств в атмосфере фононов
Аннотация
В данной работе на примере ионных кристаллов показано, что поляризация решетки кристалла разноименно заряженными поляронами (атом позитрония (Ps)) вызывает не только изменение энергии связи позитрония, но и приводит к перенормировке эффективных масс электрона и позитрона. Это взаимодействие электрона и позитрона атома позитрония с оптическими фононами приводит к дополнительному отталкивающему взаимодействию помимо кулоновского притягивающего. При этом в атмосфере фононов кристалла возможно существование атома позитрония с большими и малыми радиусами.
Введение
К настоящему времени достигнут значительный прогресс в понимании процессов взаимодействия позитронов с кристаллами, особенно с ионными, полупроводниками и металлами [1-5]. В частности, использование диаграммной техники, использование диаграммной техники уже в первом порядке теории возмущений позволяет найти величину вероятности спонтанного и вынужденного испускания и поглощения фононов позитроном [4,5]. Вычисления дают также значения собственной энергии и перенормированной массы позитронного полярона [3-5].
В данной работе на примере ионных кристаллов показано, что поляризация решетки кристалла разноименно заряженными поляронами (атом позитрония) вызывает не только изменение энергии связи позитрония, но и приводит к перенормировке эффективных масс электрона и позитрона. При этом взаимодействие электрона и позитрона атома позитрония с оптическими фононами приводит к дополнительному отталкивающему взаимодействию помимо кулоновского отталкивающего.
Прежде всего следует учесть факт, что диффузионная длина смещений позитрония в ионном кристалле составляет несколько сотен постоянной решетки. При этом поляризация решетки кристалла оказывает заметное влияние на свойства позитрония в ионных кристаллах [3]. Следует отметить также, что задача аннигиляции атома позитрония в ионных кристаллах очень похожа на аналогичную двухчастичную задачу – экситон в ионных кристаллах [6-10]. Здесь используется для решения задачи позитрония формализм Хакена [11].
Исследование позитронных и позитрониевых состояний в кристалле рамках формализма Хакена
В предыдущей главе было установлено, что существуют стационарные состояния систем позитрон (атом Рs) – кристалл, так как характерные времена протекания позитронных процессов составляют 10–16 с, ионных процессов – 10–13 с, а самое короткое время жизни относительно аннигиляции равно примерно 10-10 с. Причем позитрон и атом Рs находятся в тепловом равновесии с решеткой кристалла, т.е. они термализованы. В общем случае при облучении позитронами идеального кристалла образуются позитронные состояния следующего типа: электроны, позитроны, дырки, экситоны, атом Рs и комплексы различной природы [12]. Теория таких состояний в полупроводниках и ионных кристаллах анализировалась в рамках известных расчетных моделей квантовой физики твердого тела [1,2,11]. Удалось установить как условие стабилизации этих состояний в кристалле (например, атом Рs в идеальной кристаллической решетке), так и условие их деструкции (например, распад атома Рs при экранировании кулоновского взаимодействия между электроном и позитроном свободными носителями в полупроводниках). Теория этих состояний, однако, нуждается в более строгом обосновании и дальнейшем развитии. Наиболее эффективным методом описания свойств таких состояний является метод квантовополевой теории твердого тела [1,2,11]. Поэтому ниже в рамках этой теории дается описание свойств (эффективные массы, выражение для энергий и т.п.) позитронных состояний в идеальных кристаллах.
2. Общий подход
Изложим метод вторичного квантования для электронов и позитронов в твердом теле. Согласно [11], можем выписать выражение для одночастичных электронных и позитронных состояний в представлении вторичного квантования
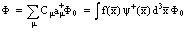 . (1)
. (1)
Здесь операторы 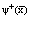 и a+ являются операторами рождения и определены в [1,2,11]; Сm – коэффициент разложения, причем
и a+ являются операторами рождения и определены в [1,2,11]; Сm – коэффициент разложения, причем 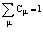 ; Ф0 – волновая функция вакуумного состояния;
; Ф0 – волновая функция вакуумного состояния; 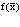 – функция, удовлетворяющая общему одночастичному уравнению Шредингера
– функция, удовлетворяющая общему одночастичному уравнению Шредингера
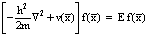 . (2.)
. (2.)
Аналогично может быть рассмотрено общее состояние двух частиц с координатами 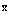 и
и 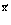
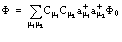 . (3)
. (3)
Причем, как и выше,
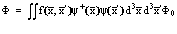 . (4)
. (4)
Выбирая стандартный гамильтониан, получаем уравнение Шредингера для двух частиц
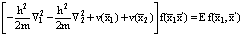 . (5)
. (5)
Эти результаты могут быть обобщены на случай многих частиц: n электронов и m позитронов.
3. Проблема многих электронов и позитронов в твердом теле
Проблема многих электронов и позитронов в рамках метода вторичного квантования может быть сформирована на основании следующей картины: электроны и позитроны движутся в строго периодическом поле решетки, ионы которой имеют бесконечно большие массы и находятся в состоянии покоя. Электроны внутренних атомных оболочек учитываются в целом тем, что они вместе с положительными атомными ядрами создают эффективный периодический решеточный потенциал V. Eстественно, что позитроны в основном движутся по периферии атомов кристалла в силу электростатического отталкивания ядрами. Оператор Гамильтона для электронов и позитронов состоит из четырех составляющих: кинетической энергии электронов (позитронов), кулоновской энергии взаимодействия электронов (позитронов) с ядрами, потенциальной энергии взаимодействия электронов (позитронов) друг с другом и кулоновской энергии взаимодействия электронов с позитронами. Cогласно [1,2,11], можно записать уравнение Шредингера для электронной и позитронной подсистем через операторы поля y+(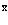 ),
),  , c+(
, c+(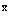 ), c(
), c(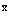 ), удовлетворяющие ферми-перестановочным соотношениям [11]. Эти операторы разлагаются по собственным функциям
), удовлетворяющие ферми-перестановочным соотношениям [11]. Эти операторы разлагаются по собственным функциям 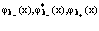 и
и 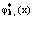 cледующим образом:
cледующим образом:
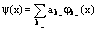 ;
; 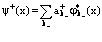 ; (6)
; (6)
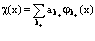 ;
; 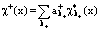 . (7)
. (7)
Отметим, что операторы поля 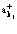 и
и 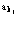 также удовлетворяют ферми-перестановочным соотношениям. Считаем, как обычно, что собственные функции
также удовлетворяют ферми-перестановочным соотношениям. Считаем, как обычно, что собственные функции 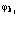 ,
, 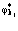 образует полный набор ортонормированных функций, но при этом их следует минимизировать так, чтобы они являлись решениями уравнения Шредингера. Для этого используется метод Хартри – Фока [130, 190, 196].
образует полный набор ортонормированных функций, но при этом их следует минимизировать так, чтобы они являлись решениями уравнения Шредингера. Для этого используется метод Хартри – Фока [130, 190, 196].
Создадим некоторое состояние Ф электронов и позитронов кристалла. Для этого расположим электроны и позитроны один за другим по состояниям к–1, к–2, …, к–n, к+1, к+2, …, к+m. Таким образом,
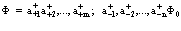 . (8)
. (8)
Используем волновую функцию (2.8) для построения среднего значения оператора Гамильтона
H = H– + H+ (9)
с дополнительным условием, что функция состояния нормирована.
Далее потребуем условия
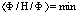 (10)
(10)
и вычислим его как функционал 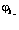 и
и 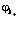 c дополнительным
c дополнительным
условием
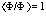 . (11)
. (11)
Затем определим 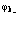 и
и  с помощью варьирования, что позволит сразу же получить уравнение Хартри – Фока для одноэлектронных и однопозитронных волновых функций кристалла
с помощью варьирования, что позволит сразу же получить уравнение Хартри – Фока для одноэлектронных и однопозитронных волновых функций кристалла
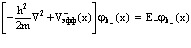 ; (12)
; (12)
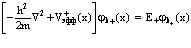 . (13)
. (13)
Здесь 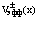 – эффективные хартри-фоковские потенциалы, включающие все виды взаимодействий, в общем случае являются периодическими с периодом решетки кристалла.
– эффективные хартри-фоковские потенциалы, включающие все виды взаимодействий, в общем случае являются периодическими с периодом решетки кристалла.
Ранее никак не уточнялось, насколько заполнены получившиеся электронные и позитронные зоны. Приведенный формализм может быть применен для случая полностью заполненной валентной зоны и соседних электронных и позитронных зон проводимости с одним электроном и одним позитроном. Имеем для функции избыточного электрона
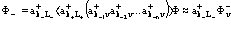 , (14)
, (14)
а для функции избыточного позитрона
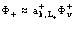 ,
, 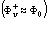 , (15)
, (15)
где L–, L+, v – индексы, относящиеся к электронным и позитронным зонам проводимости и валентной зоне соответственно. Принимаем, что
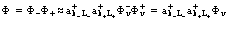 . (16)
. (16)
Далее, согласно [190, 196], легко рассмотреть применение теории Блоха к системе электронов и позитронов в кристаллической решетке и дать обоснование МЭМ, позволяющие записать полные энергии
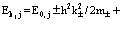
+ (члены более высокого порядка, которыми пренебрегаем). (17)
Здесь 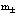 – эффективные массы электрона или позитрона. С учетом сдвига по энергии Е0 уравнение Шредингера в блоховском потенциале W± (x) записывается в виде
– эффективные массы электрона или позитрона. С учетом сдвига по энергии Е0 уравнение Шредингера в блоховском потенциале W± (x) записывается в виде
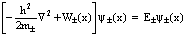 . (18)
. (18)
Решение уравнения (18) для позитрона удобнее всего анализировать в приближении Ванье [1,2,11], позволяющем описывать локализацию позитрона в окрестности точки 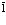 на протяжении примерно постоянной решетки. Важным свойством функций Ванье является их ортогональность, т.е. функции Ванье, локализованные в точках l и l¢ или принадлежащие различным значениям m и m¢, взаимно ортогональны
на протяжении примерно постоянной решетки. Важным свойством функций Ванье является их ортогональность, т.е. функции Ванье, локализованные в точках l и l¢ или принадлежащие различным значениям m и m¢, взаимно ортогональны
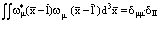 . (19)
. (19)
4. Электроны, позитроны и дырки в идеальном полупроводниковом кристалле
Формализм вторичного квантования позволяет определить электрон, позитрон и дырку как квазичастицы с эффективными массами m–, m+, mv соответственно. Для этого рассмотрим взаимодействие между электронами, дырками и позитронами на примере полупроводникового кристалла. Исследуем вопрос о форме эффективных взаимодействий при наличии удаленных из валентной зоны в зону проводимости некоторых электронов (т.е. создание в валентной зоне нескольких дырок). Причем не обязательно число дырок равно числу электронов в зоне проводимости. Их число может быть значительно больше в результате ионизации мелких примесных центров даже при комнатной температуре. Позитроны же вводятся в кристаллы, например, из b+-радиоактивного источника (Na22, Cu64 и т.д.) и образуют позитронную зону проводимости. Система такого типа описывается уравнением Шредингера НФ = EФ. Оператор Гамильтона Н, как и ранее, записываем через операторы поля 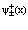 и
и 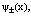 которые для рассмотрения состояний электронов в валентной зоне v, электронов и позитронов в зоне проводимости разлагаются по собственным функциям валентной зоны
которые для рассмотрения состояний электронов в валентной зоне v, электронов и позитронов в зоне проводимости разлагаются по собственным функциям валентной зоны 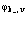 и зоны проводимости
и зоны проводимости 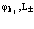 .
.
Вводим операторы рождения 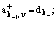
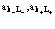 и уничтожения
и уничтожения 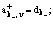
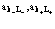 дырок, электронов и позитронов соответственно. Из соотношений (2.14), (2.15) и введенных операторов рождения и уничтожения квазичастиц следует, что дырка в валентной зоне не полностью тождественна позитрону как реальной частице. Согласно проведенным расчетам [12,13], оператор Гамильтона
дырок, электронов и позитронов соответственно. Из соотношений (2.14), (2.15) и введенных операторов рождения и уничтожения квазичастиц следует, что дырка в валентной зоне не полностью тождественна позитрону как реальной частице. Согласно проведенным расчетам [12,13], оператор Гамильтона
 , (20)
, (20)
где 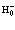 и
и 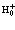 – операторы, описывающие взаимодействие лептонов в зоне проводимости и взаимодействие лептонов зоны проводимости и валентной зоны. В свою очередь
– операторы, описывающие взаимодействие лептонов в зоне проводимости и взаимодействие лептонов зоны проводимости и валентной зоны. В свою очередь
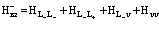 ; (21)
; (21)
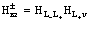 . (22)
. (22)
Здесь  - взаимодействие электронов в зоне проводимости;
- взаимодействие электронов в зоне проводимости;  - взаимодействие электронов с позитронами;
- взаимодействие электронов с позитронами; 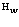 – взаимодействие дырок в валентной зоне;
– взаимодействие дырок в валентной зоне;  – взаимодействие дырок валентной зоны и позитронов в позитронной зоне проводимости.
– взаимодействие дырок валентной зоны и позитронов в позитронной зоне проводимости.
Таким образом, оператор Гамильтона для электронов, дырок и позитронов в кристалле может быть выбран в виде
H = H0 + Hвз = Нэл + Нд + Нпоз + Нэл-эл + Нэл-д + + Нпоз-д + Нэл-поз + Нд-д + Wзап, (23)
где Wзап – энергия валентной зоны.
В работах [1,2,11] были получены выражения для Hij, входящие в гамильтониан (23), через операторы рождения и уничтожения электронов, дырок и позитрона и матричные элементы энергий взаимодействия между соответствующими зонами. Выражения для энергий основного состояния электронов, позитрона и дырок для случая их нахождения вблизи краев зон записываются в виде
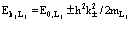 ; (24)
; (24)
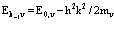 . (25)
. (25)
Сравнение (2.24) и (2.25) четко выявляет различие между позитроном и дыркой.
5. Проблема экситона, атома Рs и комплексов Уилера различной природы (позитрон-экситонные комплексы и ионы атома Рs)
С учетом приведенной выше многочастичной модели рассмотрим проблему экситонов, атома Рs и позитрон-экситонных комплексов [14,15]. Задача для общего случая позитрон-экситонного комплекса заключается опять-таки в решении уравнения Шредингера НФ = ЕФ, где гамильтониан Н описывается выражением (23).
Рассмотрим уравнение (23) для случая одного электрона, одного позитрона и одной дырки. Волновые функции электронов в состоянии k–1, позитрона в состоянии k+1 и дырки в состоянии k–2 можно получить из состояния, описывающего полностью заполненную валентную зону, последовательным действием операторов рождения 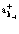 ,
,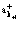 и
и 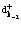 на функцию валентной зоны
на функцию валентной зоны
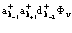 . (26)
. (26)
Из выражения (26) следует, что электрон, дырка и позитрон, пролетая друг относительно друга, испытывают взаимное рассеяние, в результате чего попадают в различные конечные состояния 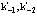 ,
,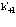 . Поэтому следует образовать функцию по всем состояниям
. Поэтому следует образовать функцию по всем состояниям 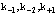 электрона, позитрона и дырки. Исходя из этого состояния, волновая функция позитрон-экситонного комплекса имеет вид:
электрона, позитрона и дырки. Исходя из этого состояния, волновая функция позитрон-экситонного комплекса имеет вид:
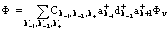 . (27)
. (27)
Гамильтониан трехчастичной системы с учетом сдвига по энергии с тем, чтобы опустить Wзап [1,2,11], состоит из выражения для кинетической энергии электрона, позитрона и дырки и взаимодействия между ними
Hобщ = Нкин + Нэл-д + Нэл-поз + Нпоз-д. (28)
Действуя оператором Нобщ на функцию Ф и выполняя соответствующие преобразования и упрощения, получаем уравнение Шредингера для позитрон-экситонного комплекса
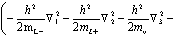
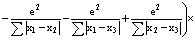
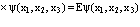 . (29)
. (29)
Позитронно-экситонный комплекс (своеобразное соединение Уилера) является аналогом классических полиэлектронных систем Уилера е–е+е– или е+е–е+ (ионы позитрония) [16, 17]. Он открыт сравнительно недавно Миллсом [18] в результате изящных экспериментов. Сродство к позитрону (электрону) атома Рs для таких комплексов составляет величину не менее 0,1 эВ, а время жизни относительно аннигиляции, согласно расчетам Ферранте [17], ровно t2g = 5,02×10–10 с. Концепция позитрон-экситонного комплекса [19,20] неоднократно использовалась для объяснения природы позитронной аннигиляции в ионных кристаллах и полупроводниках. Отметим, что из записанного выше трехчастичного уравнения (28) позитрон-экситонного комплекса легко получить уравнение для атома Рs большого радиуса и экситона Ванье в кристалле.
Ранее постулировалось утверждение о том, что расстояние между электроном, позитроном и дыркой велико, следовательно, вполне разумным является разложение операторов поля y+(x) и y(x) по блоховским функциям. Можно, однако, рассмотреть и противоположный случай, когда электрон и позитрон находятся на одном и том же атоме – атом Рs малого радиуса или позитроний Френкеля [1,2]. При этом разложение лучше всего проводить по функциям Ванье. Волновая функция Ванье позитрония Френкеля записывается в виде
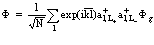 . (30)
. (30)
Здесь 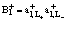 – оператор рождения локализованного в точке
– оператор рождения локализованного в точке 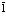 атома Ps. Разумеется, оператор его уничтожения есть
атома Ps. Разумеется, оператор его уничтожения есть 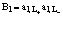 . Гамильтониан позитрония Френкеля при помощи этих операторов запишется в виде
. Гамильтониан позитрония Френкеля при помощи этих операторов запишется в виде

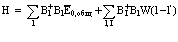 . (31)
. (31)
Действуя этим оператором на волновую функцию Ф и проводя соответствующие упрощения [1,2], получаем выражение для энергии позитрония Френкеля
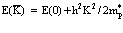 , (32)
, (32)
где 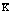 - волновой вектор позитрония;
- волновой вектор позитрония; 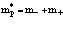 . Выражение (31) представляет собой закон дисперсии для френкелевской позитрониевой зоны в кристалле [1,2].
. Выражение (31) представляет собой закон дисперсии для френкелевской позитрониевой зоны в кристалле [1,2].
6.
Взаимодействие позитронов и атома Рs с фононами кристалла в рамках методов
вторичного квантования и функций Грина
По методу вторичного квантования в [1,2,11] было учтено взаимодействие позитронов и атома Рs с фононами кристалла. Для этого в рамках нестационарной теории возмущений в представлении взаимодействия рассмотрены процессы cпонтанного и вынужденного испускания и поглощения фононов позитроном в кристалле.
Квантованный гамильтониан Фрелиха системы записывается, как обычно [1,2,11], в виде суммы Н = Н0 + Нвз, где Н0 – гамильтониан невозмущенной задачи; Нвз рассматривается как малое возмущение.
Диаграммная техника первого порядка теории возмущений позволяет вычислить вероятность спонтанного и вынужденного испускания и поглощения фононов позитроном. Расчеты же с использованием диаграммной техники второго порядка теории возмущений позволяют найти значения собственной энергии и перенормированной массы позитрона в кристалле: 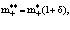 где d – сдвиг по энергии в единицах массы;
где d – сдвиг по энергии в единицах массы; 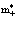 – зонная эффективная масса.
– зонная эффективная масса.
Использование теоремы о точной форме решения для взаимодействия позитрона с колебаниями решетки стационарного уравнения Шредингера НФ = ЕФ в полярных кристаллах позволяет получить выражение для энергии позитронного полярона Фрелиха [1,2,11]:
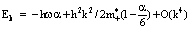 . (33)
. (33)
Откуда следует, что собственная энергия Е0 и перенормированная масса 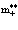 равны соответственно
равны соответственно
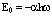 ; (34)
; (34)
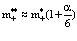 , (35)
, (35)
где a – константа связи.
Для расчетов позитронных процессов в кристаллах был использован метод функций Грина [1]. Показано, что функция Грина позитрона имеет стандартный вид
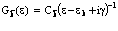 , (36)
, (36)
и является функцией 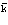 и e (здесь e имеет размерность частоты).
и e (здесь e имеет размерность частоты).
Рассмотрим функцию (36) для фиксированного 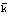 позитрона, но переменного e. Так как знаменатель в
позитрона, но переменного e. Так как знаменатель в  – комплексная величина, то эта функция отображается на комплексной e-плоскости. Эта функция имеет на комплексной плоскости один полюс, действительная координата которого равна e, а мнимая – обратному значению времени жизни. Отсюда приходим к основному понятию: полюс
– комплексная величина, то эта функция отображается на комплексной e-плоскости. Эта функция имеет на комплексной плоскости один полюс, действительная координата которого равна e, а мнимая – обратному значению времени жизни. Отсюда приходим к основному понятию: полюс  определяет энергию и время жизни позитрона (как квазичастицы) или его взаимодействие с кристаллом (окружением).
определяет энергию и время жизни позитрона (как квазичастицы) или его взаимодействие с кристаллом (окружением).
Чрезвычайно интересно применение метода функций Грина к проблеме многих электронов и позитронов в кристалле, развитое в [1].
7. Теория атома Рs в полярных кристаллах. Учет взаимодействия с фононами
Ниже показано, что поляризация решетки ионного (полярного) кристалла, не только вызывает изменение собственной энергии и перенормировку масс электрона и позитрона, но и создает дополнительное отталкивающее взаимодействие между электроном и позитроном [1].
Исходный гамильтониан атома Рs, учитывающий взаимодействие электрона и позитрона с колебаниями решетки, записывается в виде
H = Нэл + Нпоз + Нph + Hвз1 + Нвз2 +Нэл-поз. (37)
Здесь Нэл и Нпоз – операторы Гамильтона свободных электрона и позитрона,
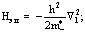
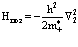 , (38)
, (38)
причем в общем случае 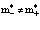 .
.
Оператор Нph описывает газ фононов (колебания решетки)
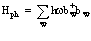 , (39)
, (39)
где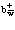 и
и  – операторы испускания (рождения) и поглощения фононов соответственно; w – частота продольных колебаний;
– операторы испускания (рождения) и поглощения фононов соответственно; w – частота продольных колебаний; 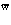 – волновой вектор фонона.
– волновой вектор фонона.
Члены, отвечающие взаимодействию электрона и позитрона с фононами, имеют вид
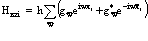 , i = 1, 2. (40)
, i = 1, 2. (40)
Гамильтониан
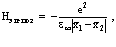 (41)
(41)
где 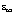 – оптическая диэлектрическая проницаемость.
– оптическая диэлектрическая проницаемость.
Задача эффективного взаимодействия электрона с позитроном (т.е. поляроном) в изложенных выше приближениях была решена методом Хакена [3-5,11]. В частности, для полной энергии имеем
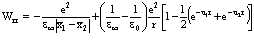 . (42)
. (42)
Здесь e0 – статическая диэлектрическая проницаемость; 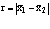 ;
;
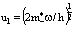 ;
; 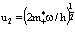 . (43)
. (43)
Из анализа выражения для полной энергии (42) следует, что для атома Рs, так же как и для экситонов, в экспериментах можно установить существование перехода от кулоновского взаимодействия с e¥ при малых радиусах атома Рs к взаимодействию с e0 при больших радиусах атома Ps.
Совершим предельный переход, т.е. полагая 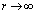 , получаем выражение для полной энергии позитрония большого радиуса
, получаем выражение для полной энергии позитрония большого радиуса
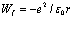
(44)
И соответственно для кинетической энергии электрона и позитрона
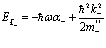 , (45)
, (45)
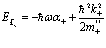 , (46)
, (46)
т.е. у электрона и позитрона, согласно Хакену [11], появляется перенормированные поляронные массы 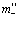 и
и 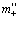 и соответственно собственные энергии
и соответственно собственные энергии 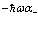 и
и 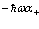 , при этом (см. также (35))
, при этом (см. также (35)) 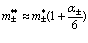 .
.
Напротив, при 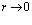 главный вклад в
главный вклад в 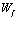 дают члены
дают члены
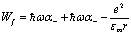 (47)
(47)
Сравнивая выражения (44), (45), (46) и (47), видим, что для позитрония, так же как и для экситона по Хакену [11], можно установить существование перехода от чисто кулоновского взаимодействия с 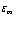 при малых радиусах позитрония к взаимодействию с
при малых радиусах позитрония к взаимодействию с 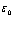 при больших расстояниях между электроном и позитроном. В последнем случае можно говорить о существовании квазипозитрония большого радиуса и о наличии перехода в некоторых случаях от квазипозитрония к обычному позитронию. Пользуясь найденными значениями перенормированных масс, путем простых действий можно легко найти характеристики позитрония как большого, так и малого радиуса соответственно. В этом направлении следует провести тщательные экспериментальные исследования.
при больших расстояниях между электроном и позитроном. В последнем случае можно говорить о существовании квазипозитрония большого радиуса и о наличии перехода в некоторых случаях от квазипозитрония к обычному позитронию. Пользуясь найденными значениями перенормированных масс, путем простых действий можно легко найти характеристики позитрония как большого, так и малого радиуса соответственно. В этом направлении следует провести тщательные экспериментальные исследования.
Список литературы
-
Прокопьев Е.П. Исследования позитронных процессов в кристаллах. М., 1982. 60 с. – Деп. в ЦНИИ”Электроника”. Р-3556. МРС ВИМИ “Техника, технология, экономика”. 1983. Сер.”ЭР”.
-
Прокопьев Е.П. Позитроны и позитроний в кристаллах. М., 1982. 138 с. – Деп. в ЦНИИ “Электроника”. Р-3475. МРС ВИМИ “Техника, технология, экономика”. №8. 1983. Сер.”ЭР”.
-
Прокопьев Е.П., Урбанович С.И. Позитроний в газе фононов // Известия АН БССР. Серия физико-математических наук. 1987. №5. С.92-94.
-
Е.П.Светлов-Прокопьев. Динамика позитронов в идеальных кристаллах. 1. Нестационарная теория возмущений (первый порядок). Подвижность и дрейф позитронов в электрическом поле. Труды XVII Международного совещания “Радиационная физика твердого тела”. (Севастополь, 9 – 14 июля 2007 г.), под редакцией заслуженного деятеля науки РФ, д.ф.-м.н., проф. Бондаренко Г.Г. М.: ГНУ «НИИ ПМТ», 2007 г., C.625-636. http://www.niipmt.ru/index.php?p=6
-
Е.П.Светлов-Прокопьев. Динамика позитронов в идеальных кристаллах. 2. Нестационарная теория возмущений второго порядка и более высших порядков. Собственная энергия и перенормировка массы позитрона. Труды XVII Международного совещания “Радиационная физика твердого тела”. (Севастополь, 9 – 14 июля 2007 г.), под редакцией заслуженного деятеля науки РФ, д.ф.-м.н., проф. Бондаренко Г.Г. М.: ГНУ «НИИ ПМТ», 2007 г., C. 637-644. http://www.niipmt.ru/index.php?p=6
-
Я.И.Френкель. Избранные труды. Т.2. М.: Наука, 1958.
-
Р.Нокс. Теория экситонов. М: Мир, 1966.
-
В.М.Агранович. Теория экситонов. М: Наука, 1968.
-
В.М.Агранович, В.Л.Гинзбург. Кристаллооптика с учетом пространственной дисперсии и теория экситонов. М: Наука, 1979.
-
Е.П.Светлов-Прокопьев. Исследование свойств атома позитрония в кристаллах.Труды XVIII Международного совещания “Радиационная физика твердого тела”. (Севастополь, 7 – 12 июля 2008 г.), под редакцией заслуженного деятеля науки РФ, д.ф.-м.н., проф. Бондаренко Г.Г. М.: ГНУ «НИИ ПМТ», 2008 г., C.?. http://www.niipmt.ru/index.php?p=6
-
Хакен Х. Квантовая теория твердого тела. М.: Наука, 1982. 262 с.
-
Прокопьев Е.П. Новые представления об аннигиляции позитронов и позитронных состояниях в полупроводниках // Химия высоких энергий. – 1994. – Т. 28, № 5. – С. 426 – 428.
- Прокопьев Е.П. Введение в теорию позитронных процессов в полупроводниках и ионных кристаллах. – М., 1979. – 384 с. – Деп. в ЦНИИ “Электроника”. Р-2837. МРС ВИМИ “Техника, технология, экономика”. – № 27. – 1980. – Сер. “ЭР”.
- Прокопьев Е.П. Комплексы Уилера в полупроводниках. – М., 1979. – 12 с. – Деп. в ЦНИИ “Электроника”. Р-2757. МРС ВИМИ “Техника, технология, экономика”. – № 28. – 1979. – Сер. “ЭР”.
-
Арефьев К.П., Прокопьев Е.П., Нурмагамбетов С.Б. Комплексы Уилера в кристаллах // Известия вузов. Физика. – 1981. – № 4.
-
Wheeler J.A. Polyelectron systems // Ann. N.Y. Acad. Sci. – 1946. – Vol. 48, № 1. – P. 219 – 226.
-
Ferrante G. Annihilation from Positronium Negative Ion e–e+e– // Phys. Rev. – 1968. – Vol. 170, № 1. – P. 76 -
80.
-
Mills A.P., Jr. // Phys. Rev. Letters- 1981. – Vol. 46, № 11. – P. 717.
-
Прокопьев Е.П. Аннигиляция позитронов и комплексы Уилера в полупроводниках // Химия высоких энергий. – 1995. – Т. 29, № 5. С. 394 – 396.
-
Арефьев К.П., Воробьев С.А., Прокопьев Е.П. Позитроника в радиационном материаловедении ионных структур и полупроводников. – М.: Энергоатомиздат, 1983. – 88 с.
Позитроны, позитроний, позитронные и позитрониевые комплексы в кристалле. ОБЗОР
III. Комплексы Уилера в полупроводниках
Аннотация
Рассмотрены процессы взаимодействия позитронов (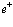 ) и позитрония (
) и позитрония (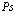 ) со свободными носителями (электронами (
) со свободными носителями (электронами (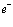 ) и дырками (
) и дырками (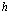 ), нейтральными (
), нейтральными (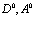 ) и заряженными (
) и заряженными (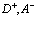 ) донорами (
) донорами (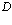 ), акцепторами (
), акцепторами (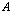 ) и экситонами (Ex) в полупроводниках. Показано, что эти процессы могут приводить к образованию комплексов Уиллера состава (
) и экситонами (Ex) в полупроводниках. Показано, что эти процессы могут приводить к образованию комплексов Уиллера состава (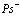 ), (
), (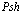 ) и более сложных комплексов
) и более сложных комплексов 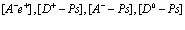 ,
, 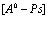 и [Ps – Ex], [Ps – Ex±], [Psh – Ex], [Pse– – Ex], [Psh – Ex±] и [Pse– – Ex±]. Расчеты основных характеристик аннигиляционных спектров комплексов Уилера показали, что времена жизни позитронов несколько “удлиняются”, а полуширины кривых УРАФ сужаются, что дает возможность наблюдать их в экспериментах.
и [Ps – Ex], [Ps – Ex±], [Psh – Ex], [Pse– – Ex], [Psh – Ex±] и [Pse– – Ex±]. Расчеты основных характеристик аннигиляционных спектров комплексов Уилера показали, что времена жизни позитронов несколько “удлиняются”, а полуширины кривых УРАФ сужаются, что дает возможность наблюдать их в экспериментах.
Экспериментальные данные по исследованию позитронных временных спектров полупроводников (см., например, [1-3]) показали, что в этих объектах наблюдается, как правило, лишь одно короткое время жизни позитронов 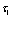 с интенсивностью
с интенсивностью 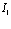 , близкой к 100%. Причем отмечалось, что существенной разницы во временах жизни
, близкой к 100%. Причем отмечалось, что существенной разницы во временах жизни 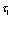 для собственного полупроводника
для собственного полупроводника 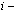 типа, полупроводников
типа, полупроводников 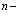 и
и 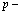 типов не наблюдалось. Впервые разницу в указанных выше различных типах полупроводников удалось установить в [4]. В этой работе были исследованы временные аннигиляционные спектры высокоомных образцов кремния
типов не наблюдалось. Впервые разницу в указанных выше различных типах полупроводников удалось установить в [4]. В этой работе были исследованы временные аннигиляционные спектры высокоомных образцов кремния 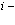 типа и низкоомных образцов кремния
типа и низкоомных образцов кремния 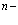 и
и 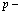 типов, легированных фосфором и бором. Было показано, что во всех образцах наблюдается лишь одна компонента
типов, легированных фосфором и бором. Было показано, что во всех образцах наблюдается лишь одна компонента 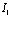 со временем жизни
со временем жизни  в пределах от 0,233 нс (собственный полупроводник
в пределах от 0,233 нс (собственный полупроводник  типа) до 0,245 нс (легированный кремний). Из данных этой работы следовало также, что различие в
типа) до 0,245 нс (легированный кремний). Из данных этой работы следовало также, что различие в 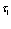 практически не наблюдалось между кремнием
практически не наблюдалось между кремнием 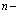 и
и 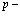 типов. Кроме того величины
типов. Кроме того величины 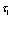 в пределах экспериментальной погрешности совпадали для кристаллов кремния, полученных методом зонной плавки и по методу Чохральского. Величины времен жизни в кремнии с собственной проводимостью (как для метода безтигельной зонной плавки, так и для метода Чохральского) были меньшими, чем в легированных образцах. Это изменение в величинах
в пределах экспериментальной погрешности совпадали для кристаллов кремния, полученных методом зонной плавки и по методу Чохральского. Величины времен жизни в кремнии с собственной проводимостью (как для метода безтигельной зонной плавки, так и для метода Чохральского) были меньшими, чем в легированных образцах. Это изменение в величинах  равно примерно 6 ± 9 % и лежит за пределами экспериментальной погрешности (порядка 2 %).
равно примерно 6 ± 9 % и лежит за пределами экспериментальной погрешности (порядка 2 %).
Этот факт говорит о том, что мелкие примесные центры донорного или акцепторного типа в полупроводниках, являющихся «поставщиками» электронов в зоне проводимости или дырок в валентной зоне, при достаточно высоких концентрациях оказывают существенное влияние на аннигиляционные временные спектры, а следовательно и на свойства квазипозитронных и квазипозитрониевых состояний [1-3]. Поэтому представляет интерес рассмотреть вопрос о процессах взаимодействия квазипозитронов 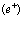 и квази –
и квази – 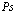 [1-3,5] (
[1-3,5] (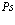 – химический символ атома позитрония [6]) с носителями и другими системами в полупроводниках и основные свойства образующихся квазипозитронных и квазипозитрониевых состояний.
– химический символ атома позитрония [6]) с носителями и другими системами в полупроводниках и основные свойства образующихся квазипозитронных и квазипозитрониевых состояний.
Рассмотрим два предельных случая. Первый, когда тепловая энергия позитрона 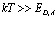 , где
, где 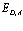 – энергия ионизации мелких доноров
– энергия ионизации мелких доноров 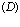 либо мелких акцепторов
либо мелких акцепторов 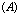 ,
, 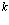 – постоянная Больцмана,
– постоянная Больцмана, 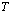 – температура. Рассмотрим процессы, в которых участвуют свободные термализованные позитроны и квази-
– температура. Рассмотрим процессы, в которых участвуют свободные термализованные позитроны и квази-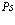 в этом случае.
в этом случае.
В этом случае свободные квазипозитроны естественно взаимодействуют с валентными электронами и свободными носителями (электронами в полупроводниках 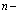 типа и дырками в полупроводниках
типа и дырками в полупроводниках 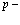 типа): а)
типа): а) 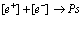 ; б)
; б) 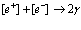 (двухквантовая аннигиляция при столкновениях квазичастиц) и в) процесс «
(двухквантовая аннигиляция при столкновениях квазичастиц) и в) процесс «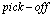 » – аннигиляции квази-
» – аннигиляции квази-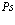 на валентных электронах, рассмотренный в [7-9].
на валентных электронах, рассмотренный в [7-9].
Сечения процессов образования квази-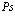 и аннигиляции позитронов при столкновениях со свободными электронами можно оценить по методу работы [10]. Например, при энергии позитрона равной 13,6 эВ вероятность образования квази-
и аннигиляции позитронов при столкновениях со свободными электронами можно оценить по методу работы [10]. Например, при энергии позитрона равной 13,6 эВ вероятность образования квази-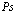 уже в 43 раза больше вероятности аннигиляции при свободных столкновениях. В свою очередь оценки [1] показали, что сечение образования квази-
уже в 43 раза больше вероятности аннигиляции при свободных столкновениях. В свою очередь оценки [1] показали, что сечение образования квази-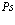 и сечение аннигиляции на валентных электронах также сопоставимы с результатами [10].
и сечение аннигиляции на валентных электронах также сопоставимы с результатами [10].
В полупроводниках 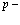 типа возможен процесс взаимодействия квазипозитрона с дырками
типа возможен процесс взаимодействия квазипозитрона с дырками 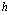 в валентной зоне, причем взаимодействие этих квазичастиц естественно будет сводиться лишь к упругому рассеянию.
в валентной зоне, причем взаимодействие этих квазичастиц естественно будет сводиться лишь к упругому рассеянию.
В полупроводниках 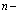 типа квази-
типа квази-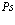 может участвовать в следущих основных процессах: а)
может участвовать в следущих основных процессах: а) 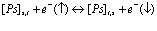 (орто-пара конверсия квази-
(орто-пара конверсия квази- , рассмотренная в [11]; б)
, рассмотренная в [11]; б)  (отрицательный ион квази-
(отрицательный ион квази- , существование и свойства которого были впервые предсказаны Уилером [12]); в)
, существование и свойства которого были впервые предсказаны Уилером [12]); в)  (процесс «
(процесс « » – аннигиляции квази-
» – аннигиляции квази- на свободных носителях и валентных электронах).
на свободных носителях и валентных электронах).
В полупроводниках 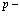 типа возможно также следующих процессов: а)
типа возможно также следующих процессов: а) 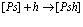 (своеобразный комплекс Уиллера [12], состоящий из электрона, позитрона и дырки); б)
(своеобразный комплекс Уиллера [12], состоящий из электрона, позитрона и дырки); б) 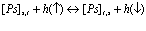 . Вопрос орто-пара-конверсии
. Вопрос орто-пара-конверсии 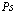 на дырках здесь не рассматривается в силу принципа тождественности этих квазичастиц(позитрона и дырки) в кристалле. Действительно, заряд позитрона и дырки одинаков, но эффективные скалярные массы не равны. Интересно отметить, что в образцах
на дырках здесь не рассматривается в силу принципа тождественности этих квазичастиц(позитрона и дырки) в кристалле. Действительно, заряд позитрона и дырки одинаков, но эффективные скалярные массы не равны. Интересно отметить, что в образцах 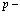 типа возможен процесс «оптической аннигиляции
типа возможен процесс «оптической аннигиляции 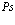 по схеме: в)
по схеме: в) 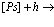 оптические кванты
оптические кванты 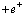 и г). Однако, по-видимому, вероятность этого процесса очень мала по сравнению с процессом «
и г). Однако, по-видимому, вероятность этого процесса очень мала по сравнению с процессом «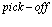 » – аннигиляции квази-
» – аннигиляции квази-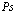 на свободных носителях и валентных электронах кристалла.
на свободных носителях и валентных электронах кристалла.
Существование комплексов Уилера 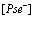 и
и 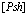 при комнатных температурах вполне реально, ибо энергии их связей составляют величины порядка несколько десятых долей эВ [12]. Их времена жизни в отношении аннигиляционного распада с учетом процесса «
при комнатных температурах вполне реально, ибо энергии их связей составляют величины порядка несколько десятых долей эВ [12]. Их времена жизни в отношении аннигиляционного распада с учетом процесса « » – аннигиляции близки короткому времени жизни
» – аннигиляции близки короткому времени жизни 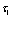 , наблюдаемому в полупроводниках [1-3].
, наблюдаемому в полупроводниках [1-3].
В другом предельном случае 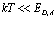 в полупроводниках
в полупроводниках  и
и 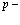 типа наряду с процессами рассеяния, «
типа наряду с процессами рассеяния, «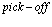 » – аннигиляции и орто-пара конверсии возможные процессы захвата квазипозитронов и квази-
» – аннигиляции и орто-пара конверсии возможные процессы захвата квазипозитронов и квази-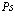 нейтральными и заряженными донорными и акцепторными состояниями с образованием сложных комплексов Уилера:
нейтральными и заряженными донорными и акцепторными состояниями с образованием сложных комплексов Уилера: 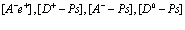 и
и 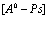 , где
, где 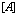 – символ акцептора, а
– символ акцептора, а 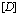 – донора.
– донора.
Таким образом, все квазпозитронные и квазипозитрониевые состояния , а также комплексы Уиллера могут быть разбиты на две основные группы: а)делокализованные состояния и б) локализованные состояния. В табл.1 приведена условная классификация этих состояний и их аналоги, как это, например, было сделано Лампертом [13] для комплексов, включающих в свой состав электрон 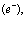 дырки
дырки 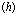 и экситоны
и экситоны 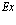 .
.
Таблица 1
Возможные типы позитронных и позитрониевых состояний и комплексы Уилера в полупроводниках
|
Тип состояния |
Аналоги |
Возможный температурный интервал наблюдения |
|
I. Нелокализованные состояния |
||
|
Комплексы Уилера
|
Ионы Молекулы Ионы молекул
|
Комнатная Комнатная и ниже Комнатная и ниже От комнатной до температуры жидкого гелия |
|
II. Локализованные комплексы Уилера |
||
|
|
Акцепторные состояния Экситоны, связанные с заряженными и нейтральными донорами и акцепторами |
От комнатной до температуры жидкого гелия |
Изложим ниже основные положения теории позитронных состояний в дефектных кристаллах полупроводников. Вначале рассмотрим полупроводники с мелкими примесными центрами с достаточно идеальной кристаллической решеткой (т.е. реальные полупроводники) [1-3, 5, 14-16]. В таких полупроводниках наибольший интерес представляет взаимодействие позитронов е+ и атома Ps со свободными носителями, локализованными и делокализованными комплексами, такими как нейтральные доноры 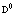 ; акцепторы
; акцепторы 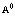 ; экситоны Ex; заряженные доноры
; экситоны Ex; заряженные доноры 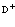 и акцепторы
и акцепторы 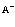 ; ионы экситона
; ионы экситона 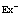 ; биэкситоны
; биэкситоны 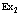 ;
; 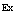 , связанные с
, связанные с 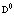 ,
, 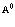 ,
, 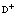 ,
, 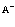 и т.д. В этом случае могут образовываться довольно своеобразные комплексы Уилера [2, 17], включающие в свой состав e+ и
и т.д. В этом случае могут образовываться довольно своеобразные комплексы Уилера [2, 17], включающие в свой состав e+ и 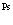 . Из аннигиляционных характеристик таких комплексов также можно, в принципе, получить полезную информацию об электронно-дырочных комплексах в полупроводниках. Приведем основные сведения о делокализованных комплексах Уилера [2, 17].
. Из аннигиляционных характеристик таких комплексов также можно, в принципе, получить полезную информацию об электронно-дырочных комплексах в полупроводниках. Приведем основные сведения о делокализованных комплексах Уилера [2, 17].
Комплексы [Pse–] и [Psh]. Заметим, что 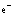 и h – символы носителей – электронов и дырок в полупроводниках соответственно. Для оценок свойств этих комплексов можно принять, что
и h – символы носителей – электронов и дырок в полупроводниках соответственно. Для оценок свойств этих комплексов можно принять, что 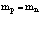 , т.е.
, т.е. 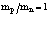 . Здесь и далее
. Здесь и далее 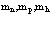 - эффективные массы электрона, позитрона и дырки соответственно. Расчеты дают [5,13] для системы [Pse–] энергию диссоциации относительно распада на
- эффективные массы электрона, позитрона и дырки соответственно. Расчеты дают [5,13] для системы [Pse–] энергию диссоциации относительно распада на 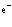 и Ps
и Ps 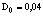 эВ. Время жизни этого комплекса относительно двухквантового аннигиляционного распада по оценкам [1-3] составляет величину
эВ. Время жизни этого комплекса относительно двухквантового аннигиляционного распада по оценкам [1-3] составляет величину 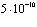 с. Для комплекса [Psh] могут встретиться случаи: а)
с. Для комплекса [Psh] могут встретиться случаи: а) 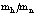 >> 1 и
>> 1 и 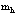 >>
>>
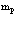 (эта система похожа по своим свойствам на квазиатомную систему атом водорода плюс позитрон (
(эта система похожа по своим свойствам на квазиатомную систему атом водорода плюс позитрон (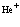 ) [15]; энергия диссоциации такой системы составляет величину
) [15]; энергия диссоциации такой системы составляет величину 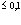 эВ); б)
эВ); б) 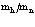 << 1 и
<< 1 и  << 1 (в этом случае можно рассматривать движение легкой дырки в поле неподвижного диполя конечной длины [18-20]; энергия диссоциации такой системы не превышает величину нескольких сотых долей электрон-вольта). Вероятнее всего в обоих случаях время жизни комплекса [Psh] относительно самоаннигиляции не превышает величину порядка
<< 1 (в этом случае можно рассматривать движение легкой дырки в поле неподвижного диполя конечной длины [18-20]; энергия диссоциации такой системы не превышает величину нескольких сотых долей электрон-вольта). Вероятнее всего в обоих случаях время жизни комплекса [Psh] относительно самоаннигиляции не превышает величину порядка 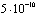 с [15].
с [15].
Комплексы Уилера [Ps – Ex], [Ps – Ex±], [Psh – Ex], [Pse– – Ex], [Psh – Ex±] и [Pse– – Ex±]. Существование комплексов Уилера такого типа возможно в интервале температур  в полупроводниках n- и p-типа (
в полупроводниках n- и p-типа (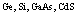 и др.) с высокой концентрацией экситонов. Система [Ps – Ex]
и др.) с высокой концентрацией экситонов. Система [Ps – Ex]
является аналогом как молекулы (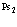 ) [17,21,22], так и биэкситона
) [17,21,22], так и биэкситона 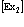 (см., например, [23-25]. В простейшем приближении
(см., например, [23-25]. В простейшем приближении 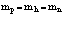 . Этот комплекс можно рассматривать как модель из атомов Ps, в которой каждый атом действует, как электрический диполь конечной длины, что приводит к притяжению между диполями [21]. В этом приближении энергия связи такой системы составляет величину 0,55 эВ, а межатомное расстояние –
. Этот комплекс можно рассматривать как модель из атомов Ps, в которой каждый атом действует, как электрический диполь конечной длины, что приводит к притяжению между диполями [21]. В этом приближении энергия связи такой системы составляет величину 0,55 эВ, а межатомное расстояние – 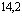
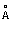 . Вариационные расчеты по Оре [26], Хиллерасу и Оре [27] дают энергии связи 0,135 и 0,11 эВ соответственно, а Шармы [22] – 0,948 эВ. Заметим, что время жизни комплекса относительно самоаннигиляции в этом случае также не должно превышать величину порядка 0,5 нс [1]. Таким образом, в этом приближении можно с полной уверенностью говорить о возможности существования комплекса [Ps – Ex] в полупроводниках (по аналогии с работой [23] для случая
. Вариационные расчеты по Оре [26], Хиллерасу и Оре [27] дают энергии связи 0,135 и 0,11 эВ соответственно, а Шармы [22] – 0,948 эВ. Заметим, что время жизни комплекса относительно самоаннигиляции в этом случае также не должно превышать величину порядка 0,5 нс [1]. Таким образом, в этом приближении можно с полной уверенностью говорить о возможности существования комплекса [Ps – Ex] в полупроводниках (по аналогии с работой [23] для случая 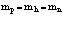 ).
).
Рассмотрим некоторые другие случаи, которые могут встретиться для условий существования комплексов [Ps – Ex]. Это случай 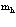 ~
~
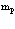 и
и 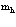 >>
>>
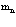 ,
, 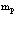 >>
>>
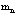 . Такого рода системы ближе по своим свойствам к молекуле водорода
. Такого рода системы ближе по своим свойствам к молекуле водорода 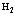 . В другом предельном случае
. В другом предельном случае 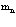 >>
>>
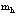 и
и 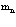 >>
>>
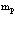 имеем аналогию с молекулой антиводорода
имеем аналогию с молекулой антиводорода 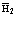 . Ее характеристики примерно такие же, как и молекулы
. Ее характеристики примерно такие же, как и молекулы 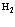 . Общий случай
. Общий случай 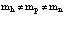 для комплекса [Ps – Ex]
для комплекса [Ps – Ex]
может быть рассмотрен вариационным методом, как это делалось для 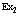 [24,25]. Расчеты экситонных молекул для случаев анизотропных “легких” электронных масс
[24,25]. Расчеты экситонных молекул для случаев анизотропных “легких” электронных масс 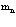 и “тяжелых” дырок с анизотропной эффективной массой
и “тяжелых” дырок с анизотропной эффективной массой 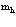 показали возможность существования этих молекул, а следовательно, по аналогии с ними комплексов Уилера [Ps – Ex]
показали возможность существования этих молекул, а следовательно, по аналогии с ними комплексов Уилера [Ps – Ex]
для различных величин 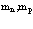 и
и 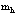 .
.
Приведем основные результаты для комплексов Уилера 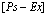 . Имея значения общей энергии системы
. Имея значения общей энергии системы 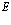 для различных значений
для различных значений 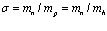 , дадим общий анализ процессов связывания и распада комплексов Уиллера этого типа. В частности, энергия связи комплекса
, дадим общий анализ процессов связывания и распада комплексов Уиллера этого типа. В частности, энергия связи комплекса 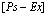 в отношении распада на
в отношении распада на 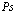 и
и 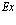 будет равна
будет равна
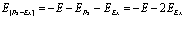 , (1)
, (1)
где 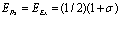 – энергия связи атома позитрония и экситона.
– энергия связи атома позитрония и экситона.
Расчеты энергий связи комплексов Уилера [Ps – Ex±], [Psh – Ex], [Pse– – Ex], [Psh – Ex±] и [Pse– – Ex±] еще более сложны по сравнению с расчетами комплексов [Ps – Ex]. Однако асимптотические случаи 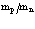 >> 1 и
>> 1 и 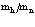 >> 1 либо, наоборот,
>> 1 либо, наоборот, 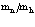 >> 1 и
>> 1 и 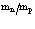 >> 1 показывают, что такие образования можно рассматривать как квазимолекулярные системы, подобные
>> 1 показывают, что такие образования можно рассматривать как квазимолекулярные системы, подобные 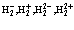 . Сопоставление свойств таких квазимолекулярных систем с обычными молекулярными ионами дает основание полагать, что в некоторых случаях такие системы могут быть динамически стабильными. Далее рассмотрим некоторые локализованные комплексы в полупроводниках, включающие в свой состав позитроны и атом Ps.
. Сопоставление свойств таких квазимолекулярных систем с обычными молекулярными ионами дает основание полагать, что в некоторых случаях такие системы могут быть динамически стабильными. Далее рассмотрим некоторые локализованные комплексы в полупроводниках, включающие в свой состав позитроны и атом Ps.
Мелкие акцепторные позитронные состояния. Позитроны при низких температурах могут захватываться на мелкие акцепторные уровни. Такого рода состояния обычно рассматриваются в приближении метода эффективной массы (МЭМ) с поправками на ход потенциала в непосредственной близости от примесного центра. В этом случае энергия связи позитрона не превышает, как правило, нескольких сотых долей электрон-вольта.
Комплексы Уилера 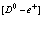 или
или 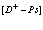 ,
, 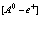 или
или 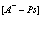 ,
, 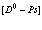 и
и 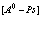 . Оценим основные параметры комплексов Уилера такого типа в приближении МЭМ. Вначале проведем оценки для случая комплексов
. Оценим основные параметры комплексов Уилера такого типа в приближении МЭМ. Вначале проведем оценки для случая комплексов 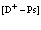 и
и 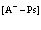 . Как было показано [17], энергия связи этих комплексов зависит от параметра
. Как было показано [17], энергия связи этих комплексов зависит от параметра 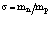 и описывается выражением
и описывается выражением
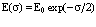 . (2)
. (2)
Зная экспериментальное значение 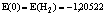 (а.е. МЭМ), можно легко построить зависимость
(а.е. МЭМ), можно легко построить зависимость 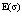 от
от 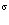 . Полученные в экспериментах значения энергий связи систем
. Полученные в экспериментах значения энергий связи систем 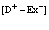 для ряда полупроводников
для ряда полупроводников 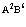 и
и  расходятся в области значений энергий, вычисленных по формуле (2) для систем Уилера. При этом из оценок нижней и верхней границ энергий связи критическая величина определяется неравенством
расходятся в области значений энергий, вычисленных по формуле (2) для систем Уилера. При этом из оценок нижней и верхней границ энергий связи критическая величина определяется неравенством 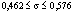 .
.
Выражение для энергий систем  и
и 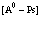 в приближении МЭМ определяется следующим образом:
в приближении МЭМ определяется следующим образом:
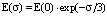 . (3)
. (3)
Отсюда легко получить зависимость 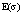 от
от  , если использовать экспериментальные значения
, если использовать экспериментальные значения 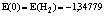 (а.е. МЭМ). Условия стабильности этого типа комплексов выражаются неравенством
(а.е. МЭМ). Условия стабильности этого типа комплексов выражаются неравенством 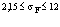 . Сопоставление расчетных значений Е по формуле (4.8) и экспериментальных значений энергий для комплексов
. Сопоставление расчетных значений Е по формуле (4.8) и экспериментальных значений энергий для комплексов 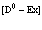 ,
, 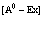 или
или 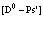 ,
, 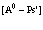 решает положительным образом возможность их существования в полупроводниках, по крайней мере, при низких температурах. Например, в
решает положительным образом возможность их существования в полупроводниках, по крайней мере, при низких температурах. Например, в 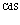 при
при 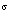 @
@ энергия связи комплексов
энергия связи комплексов 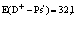 мэВ, а
мэВ, а 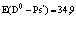 мэВ. Дальнейшее усложнение комплексов Уилера вида
мэВ. Дальнейшее усложнение комплексов Уилера вида 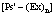 приводит, по существу, к необходимости расчета аннигиляции позитронов в конденсированных экситонных каплях (Л.В.Келдыш, 1971 г.) [28, 29].
приводит, по существу, к необходимости расчета аннигиляции позитронов в конденсированных экситонных каплях (Л.В.Келдыш, 1971 г.) [28, 29].
Расчеты основных характеристик аннигиляционных спектров комплексов Уилера показали [2,17], что времена жизни позитронов несколько “удлиняются”, а полуширины кривых УРАФ сужаются. Однако эти эффекты не столь значительны и поэтому экспериментальное наблюдение комплексов Уилера представляет собой довольно трудную задачу, так как все измерения следует проводить при температурах жидкого гелия и на установках с максимальным разрешением. Все же проблема комплексов Уилера в полупроводниках и других веществах настолько важна, что будущие эксперименты в этом направлении неизбежны.
Заключение. Рассмотрены два предельных случая взаимодействия позитронов и позитрония со свободными носителями в полупроводниках. Первый, когда тепловая энергия позитрона 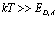 , где
, где 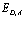 – энергия ионизации мелких доноров
– энергия ионизации мелких доноров 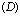 либо мелких акцепторов
либо мелких акцепторов 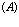 ,
, 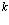 – постоянная Больцмана,
– постоянная Больцмана, 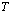 – температура. В этом случае свободные позитроны естественно взаимодействуют с валентными электронами и свободными носителями (электронами в полупроводниках
– температура. В этом случае свободные позитроны естественно взаимодействуют с валентными электронами и свободными носителями (электронами в полупроводниках 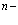 типа и дырками в полупроводниках
типа и дырками в полупроводниках 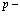 типа): а)
типа): а) 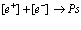 ; б)
; б) 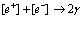 (двухквантовая аннигиляция при столкновениях квазичастиц) и в) процесс «
(двухквантовая аннигиляция при столкновениях квазичастиц) и в) процесс «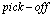 » – аннигиляции позитрония (
» – аннигиляции позитрония (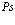 ) на валентных электронах. В полупроводниках
) на валентных электронах. В полупроводниках 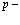 типа возможен процесс взаимодействия квазипозитрона с дырками
типа возможен процесс взаимодействия квазипозитрона с дырками 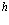 в валентной зоне, причем взаимодействие этих квазичастиц естественно будет сводиться лишь к упругому рассеянию. В полупроводниках
в валентной зоне, причем взаимодействие этих квазичастиц естественно будет сводиться лишь к упругому рассеянию. В полупроводниках 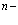 типа
типа 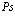 участвовать в следущих основных процессах: а)
участвовать в следущих основных процессах: а) 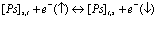 (орто-пара конверсия
(орто-пара конверсия  ; б)
; б) 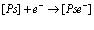 (отрицательный ион
(отрицательный ион  , существование и свойства которого были впервые предсказаны Уилером); в)
, существование и свойства которого были впервые предсказаны Уилером); в) 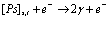 (процесс «
(процесс « » – аннигиляции квази-
» – аннигиляции квази- на свободных носителях и валентных электронах). В полупроводниках
на свободных носителях и валентных электронах). В полупроводниках  типа возможно также следующих процессов: а)
типа возможно также следующих процессов: а) 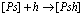 (своеобразный комплекс Уиллера, состоящий из электрона, позитрона и дырки). Существование комплексов Уилера
(своеобразный комплекс Уиллера, состоящий из электрона, позитрона и дырки). Существование комплексов Уилера 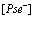 и
и 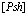 при комнатных температурах вполне реально, ибо энергии их связей составляют величины порядка несколько десятых долей эВ. В другом предельном случае
при комнатных температурах вполне реально, ибо энергии их связей составляют величины порядка несколько десятых долей эВ. В другом предельном случае 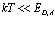 в полупроводниках
в полупроводниках 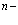 и
и 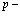 типа наряду с процессами рассеяния, «
типа наряду с процессами рассеяния, «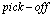 » – аннигиляции и орто-пара конверсии возможные процессы захвата позитронов и
» – аннигиляции и орто-пара конверсии возможные процессы захвата позитронов и 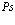 нейтральными и заряженными донорами и акцепторами с образованием сложных комплексов Уилера:
нейтральными и заряженными донорами и акцепторами с образованием сложных комплексов Уилера: 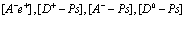 и
и 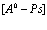 , где
, где 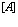 – символ акцептора, а
– символ акцептора, а 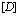 – донора. Таким образом, все квазпозитронные и квазипозитрониевые состояния , а также комплексы Уиллера могут быть разбиты на две основные группы: а)делокализованные состояния и б) локализованные состояния. Наряду с этим возможно существование комплексов Уилера [Ps – Ex], [Ps – Ex±], [Psh – Ex], [Pse– – Ex], [Psh – Ex±] и [Pse– – Ex±], где Ex – символ экситона. Существование комплексов Уилера такого типа возможно в интервале температур
– донора. Таким образом, все квазпозитронные и квазипозитрониевые состояния , а также комплексы Уиллера могут быть разбиты на две основные группы: а)делокализованные состояния и б) локализованные состояния. Наряду с этим возможно существование комплексов Уилера [Ps – Ex], [Ps – Ex±], [Psh – Ex], [Pse– – Ex], [Psh – Ex±] и [Pse– – Ex±], где Ex – символ экситона. Существование комплексов Уилера такого типа возможно в интервале температур 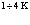 в полупроводниках n- и p-типа (
в полупроводниках n- и p-типа (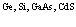 и др.) с высокой концентрацией экситонов. Расчеты основных характеристик аннигиляционных спектров комплексов Уилера показали, что времена жизни позитронов несколько “удлиняются”, а полуширины кривых УРАФ сужаются, что дает возможность наблюдать их в экспериментах.
и др.) с высокой концентрацией экситонов. Расчеты основных характеристик аннигиляционных спектров комплексов Уилера показали, что времена жизни позитронов несколько “удлиняются”, а полуширины кривых УРАФ сужаются, что дает возможность наблюдать их в экспериментах.
Список литературы
-
Прокопьев Е.П., Кузнецов Ю.Н., Хашимов Ф.Р. Основы позитроники полупроводников. М.,1976. 343 с. – Деп. в ЦНИИ “Электроника”. Р-2073. РИ.77.06.3412.
-
Прокопьев Е.П. Введение в теорию позитронных процессов в полупроводниках и ионных кристаллах. М., 1979. 384 с. – Деп. в ЦНИИ “Электроника”. Р-2837. МРС ВИМИ “Техника, технология, экономика”. №27. 1980. Сер.”ЭР”.
-
Арефьев К.П., Воробьев С.А., Прокопьев Е.П. Позитроника в радиационном материаловедении ионных структур и полупроводников. М.: Энергоатомиздат, 1983. 88 с.
-
P.Sen, C.Sen //J. Phys. 1974. Vol.C7. P.2776.
-
Е.П.Прокопьев, С.П.Тимошенков, В.И.Графутин, Г.Г.Мясищева, Ю.В.Фунтиков. Позитроника ионных кристаллов, полупроводников и металлов. М.: Ред.-изд. отдел МИЭТ (ТУ), 1999. 176 с.
-
В.И.Гольданский. Физическая химия позитронов и позитрония. М.: Наука, 1968.
-
Прокопьев Е.П. Об аномальных свойствах атома позитрония (Ps) в ионных кристаллах и полупроводниках // Физика твердого тела. 1977. Т.19. Вып.2. С.472-475.
-
Прокопьев Е.П. Позитроний и его свойства в полупроводниках и щелочно-галоидных кристаллах // Химия высоких энергий. 1978. Т.12. Вып.2. С.172-174.
-
W.Brandt, J.Reinheimer // Phys. Rev. 1970. Vol.B8. P.3104.
-
Д.Иваненко, А.Соколов // ДАН СССР. 1978. Т.239. С.1082.
-
Варисов А.З., Кузнецов Ю.Н., Прокопьев Е.П. Почему в полупроводниках наблюдается одно короткое время жизни позитронов // ДАН СССР. 1978. Т.239. №5. С.1082-1085.
-
J.Wheeler // Ann. N. Y. Acad. Sci, 1946. Vol,48. P.219.
-
M.A.Lampert // Phys. Rev. Lett. 1958. Vol.1, P.450.
-
Кузнецов Ю.Н., Прокопьев Е.П., Варисов А.З. Основы теории позитронных состояний в ионных кристаллах. – М., 1978. – 292 с. – Деп. в ЦНИИ “Электроника”, Р-2382. Сб. ВИМИ “Военная техника и экономика”. Сер. общетехническая. – № 14. – 1978.
-
Варисов А.З., Арефьев К.П., Воробьев А.А., Кузнецов Ю.Н., Прокопьев Е.П. Позитроны в конденсированных средах. – М., 1977. – 489 с. – Деп. в ЦНИИ “Электроника”. Р-2317. Сб. ВИМИ “Военная техника и экономика”. Сер. общетехническая. – № 9. – 1978.
-
Прокопьев Е.П. Исследования в области физики медленных позитронов. Позитронная аннигиляция – новый метод изучения строения вещества. – М., 1986. – 86 с. – Деп. в ЦНИИ “Электроника”. Р-4367. Сб. реф. НИОКР, обзоров, переводов и деп. рукописей. Сер. “ИМ”. – №12. – 1987.
-
Прокопьев Е.П. Комплексы Уилера в полупроводниках. – М., 1979. – 12 с. – Деп. в ЦНИИ “Электроника”. Р-2757. МРС ВИМИ “Техника, технология, экономика”. – № 28. – 1979. – Сер. “ЭР”.
-
В.Н.Абакумов, В.И.Перель, И.Н.Яссиевич // ФТП. 1978. Т.12. С.3.
-
В.Н.Абакумов, И.Н.Яссиевич // ЖЭТФ. 1976. Т.71. С.657.
-
В.Н.Абакумов, В.И.Перель, И.Н.Яссиевич // ЖЭТФ. 1977. Т.72. С.674.
-
G.T.Hill // NuovoCimento. 1972. Vol.10B. P.511.
-
R.R.Sharma // Phys. Rev. 1968. Vol.171. P.36.
-
J.R.Haynes // Phys. Rev. Lett. 1966. Vol.17. P.860.
-
O.Akimoto, E.Hanamura // J. Phys. Soc. Japan. 1972. Vol.33. P.1537.
-
O.Akimoto // J. Phys. Soc. Japan. 1973. Vol.35. P.973.
-
A.Ore // Univ. Bergen Arbook. №9, №12. 1949.
-
E.Hylleraas, A.Ore // 1947. Vol.71. P.493.
-
Л.В.Келдыш // УФН. 1970. Т.100. С.514.
-
Л.В.Келдыш // В сб. Экситоны в полупроводниках. М.: Наука, 1971. С.5.


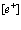
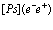
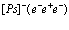
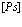

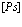
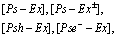
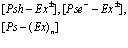
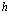

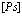 и
и 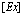
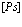 и
и