Хотя лед и относится к числу давно известных материалов, однако его свойства изучены еще далеко не достаточно. Именно поэтому многие современные исследования направлены на решение различных проблем, связанных с образованием льда.
Так, проблемы защиты искусственных и природных покрытий от различных видов намерзания, создающего угрозу жизнедеятельности людей и безопасной эксплуатации технических сооружений, рассмотрены в работе [1].
В работе [2] развивается серия публикаций о конечноэлементном моделировании контактного взаимодействия ледяного покрова с некоторыми конструкциями и средами. Проведен сравнительный анализ результатов моделирования контакта ледяных образований с учетом гидродинамики на базе выбранного CAE-алгоритма контактного взаимодействия льда с водой.
В работе [3] рассмотрена математическая модель замерзания воды в замкнутом объеме с учетом растворенных газов, учитывающая изменение сжимаемости среды из-за выделения газа. Разработана математическая модель замерзания воды, учитывающая влияние выделения растворенного газа на динамику роста давления. Создана программа численного решения поставленной задачи с фазовым переходом «вода – лед». Выявлен ряд закономерностей в динамике замерзания и роста давления в замкнутых объемах, не описывающихся ранее другими моделями, не учитывающими фактор растворенного газа.
В статье [4] проанализирован ряд алгоритмов современных CAE-систем для целей конечноэлементного моделирования контактного взаимодействия льда и металлической конструкции, а также отдельных ледяных образований между собой. Обсуждены особенности применения этого алгоритма в задачах прогнозирования поведения льда.
Некоторые другие задачи с подвижными границами также рассмотрены в работах [5, 6], посвященных изучению разложения газовых гидратов в природных пластах.
В рассматриваемой работе автором поставлена простая задача (с подвижной границей) одномерного моделирования процесса образования льда при контакте холодного тела и жидкости на основе уравнений теплопроводности.
Рассмотрим полубесконечное холодное твердое тело, контактирующее с жидкостью (например, водой). В плоскости контакта тела с жидкостью (координата ) начинается процесс образования льда. При этом мы имеем дело с подвижной границей, на которой происходит прирост нового слоя льда (координата ). Схема образования льда приведена на рис. 1. Здесь в области  находится твердое тело, в области  расположен слой образующегося льда, а в области  находится жидкость.
Необходимо выяснить, как изменяется координата , определяющая толщину слоя льда, со временем. Для этого нужно решить температурную задачу для контактирующих сред.

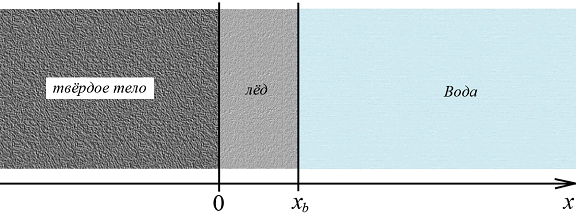
Рисунок 1 – Схема образования льда с подвижной границей

Для описания распределения температур в рассматриваемых зонах воспользуемся уравнениями теплопроводности:
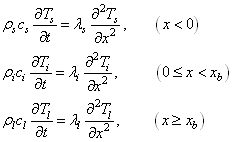 (1)
где  – плотность,  – удельная теплоемкость,  – теплопроводность; нижний индекс  относится к твердому телу, льду и жидкости соответственно.
На границах раздела сред «твердое тело – лед» и «лед – жидкость» имеют место условия равенства температур и тепловых потоков, математическая запись которых имеет вид:
 (2)
где  – удельная теплота плавления льда,  – температура кристаллизации. Температуру  на границе раздела «твердое тело – лед» будем считать постоянной .
Будем считать, что в начальный момент времени  температуры твердого тела и жидкости однородны и равны соответственно  и .
В такой постановке задача допускает введение автомодельной переменной  в виде , где  – коэффициент температуропроводности льда. Координата границы, на которой происходит образование льда, в этом случае найдется как , а скорость ее движения  найдется как .
Система уравнений теплопроводности (1) в рамках введенных обозначений примет следующий вид:
 (3)
Здесь  и  – коэффициенты температуропроводности для твердого тела и жидкости соответственно.
Решения этой системы имеют вид:
 (4)
В решениях (4) неизвестными величинами являются координата границы льдообразования  и температура . Определить их можно на основе системы условий (2) баланса тепловых потоков на границах раздела сред, предварительно записанной в автомодельных координатах. С учетом полученных решений (4) для распределения температур, система (2) примет вид:
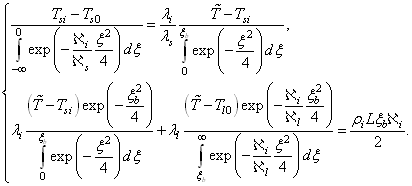 (5)
Записанная система уравнений легко решается средствами системы MathCAD.
На основе полученных решений о распределении температур в системе «твердое тело – лед – жидкость» проанализируем влияние параметров такой системы на динамику образования слоя льда.
На рис. 2 показана зависимость температуры в системе «железо – лед – вода» от автомодельной координаты  при различных начальных температурах твердого тела. Начальная температура воды во всех случаях . Линия 1 соответствует температуре железа , линия 2 – температуре железа , и линия 3 – температуре железа . При этом для соответствующих температур и координат границы образования льда имеем: ,  (линия 1); ,  (линия 2); ,  (линия 3). Толщина слоя льда по истечении 24 часов в случае  будет составлять около 22,1 см, а в случае  – около 15,6 см.

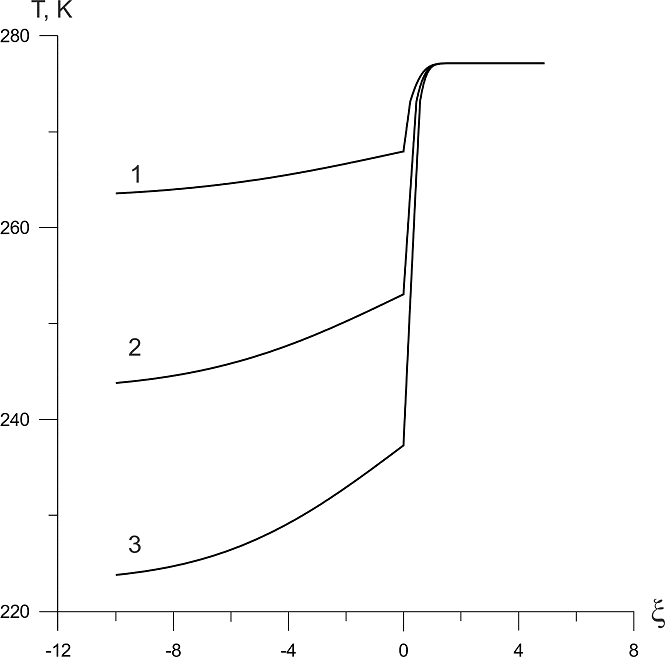
Рисунок 2 – Профили температур для системы «железо – лед – вода»: линия 1 – , линия 2 – , линия 3 – 

Из графиков видно, что выравнивание температур в твердом теле для всех случаев примерно одинаково, тогда как градиент падения температуры больше в случае более низких температур тела. Выравнивание температур во льду и воде происходит достаточно быстро.
На рис. 3 показана зависимость температуры в системе «твердое тело – лед – вода» от автомодельной координаты для различных материалов твердого тела. Начальная температура воды во всех случаях , начальная температура твердого тела . Линия 1 соответствует алюминию, линия 2 – меди, и линия 3 – железу. Соответствующие температуры и координаты границ образования льда: для линии 1 – , , для линии 2 – , , для линии 3 – , . Толщина слоя льда через 24 часа в этих трех случаях при  будет составлять 23,3 см, 24,4 см и 22,1 см соответственно.

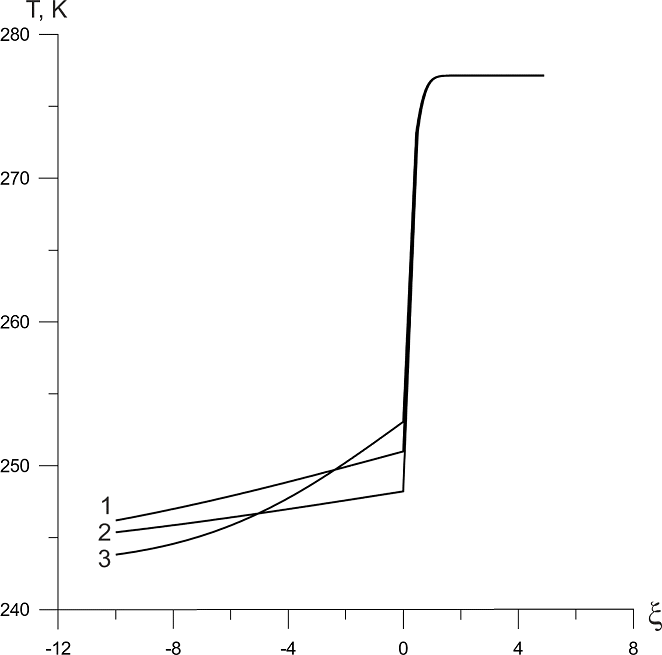
Рисунок 3 – Профили температур для системы «твердое тело – лед – вода»: линия 1 – алюминий, линия 2 – медь, линия 3 – железо

Из графиков также видно, что выравнивание температур в твердом теле для разных случаев сильно отличается: быстрее всего выравнивается температура в железе. Это объясняется более низким коэффициентом теплопроводности железа по сравнению с алюминием и медью. Поэтому температурная волна в железе не успевает достаточно глубоко проникнуть.
На рис. 4 показана зависимость координаты границы образования льда  от начальной температуры твердого тела  для систем «медь – лед – вода» (линия 1) и «железо – лед – вода» (линия 2). Начальная температура воды . Видно, что для одних и тех же начальных температур твердого тела координата границы образования льда больше в случае меди, что, как уже было сказано выше, объясняется более высокой теплопроводностью меди. С ростом температуры твердого тела отмеченная разность координат границ образования льда постепенно уменьшается.

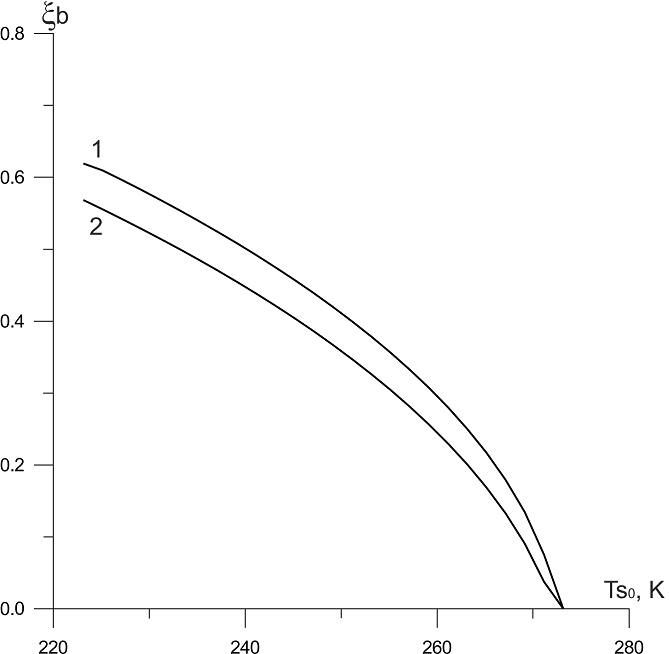
Рисунок 4 – Зависимость координаты границы образования льда  от температуры твердого тела  для систем «медь – лед – вода» (линия 1) и «железо – лед – вода» (линия 2).

Таким образом, получили ожидаемые выводы о том, что при одной и той же температуре холодного твердого тела и жидкости скорость роста ледяного слоя сильно зависит от теплопроводности твердого тела: для более теплопроводного твердого тела процесс льдообразования идет более интенсивно.
Кроме того, в работе получено, что образование ледяного слоя возможно только в случаях, если температуры твердого тела и жидкости удовлетворяют следующему условию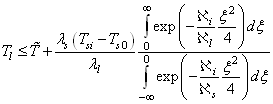. (6)В частном случае, когда в качестве жидкости выступает вода, условие образования льда (6) может быть переписано в виде

,

т.к. для воды температуры  и  в этом случае одинаковы, и равны ; при этом  и  выражены в градусах Цельсия.
Так, например, в случае, когда в качестве холодного твердого тела выступает железо при температуре , образование льда на границе раздела «железо – вода» возможно, если только температура воды удовлетворяет условию . В противном случае лед образовываться не будет.
На основе приведенной простейшей модели образования льда при контакте жидкости с холодным телом, можно строить другие более сложные модели. Например, можно учитывать наличие источников тепла, рассматривать ограниченные области, рассмотреть указанную задачу в условиях радиальной симметрии, и т.д.

1. Лапшин В.Б., Палей А.А., Жохова Н.В., Соколов В.А., Смирнов А.Н., Балышев А.В. Экспериментальные исследования методов защиты от обледенения // Исследовано в России: электронный научный журнал. 2007. [Электронный ресурс]. – Режим доступа: http://zhurnal.ape.relarn.ru/articles/2007/107.pdf
2. Лобанов В.А. Гидродинамика льда в задачах с конечноэлементной постановкой // Дифференциальные уравнения и процессы управления: электронный журнал. 2010. №1. – С. 10-17.
3. Самылова Ю.А. Численное моделирование замерзания воды с растворенным газом в замкнутых объемах: автореф. дис. … канд. физ.-мат. наук. – Тюмень: Сургутский гос. пед. ун-т. 2010. – 18 с.
4. Лобанов В.А. Моделирование взаимодействия льда с конструкциями // Вестник научно-технического развития. 2011. № 10 (50). – С. 31 – 39.
5. Шагапов В.Ш., Насырова Л.А., Потапов А.А., Дмитриев В.Л. Тепловой удар под воздействием энергии излучения на пористую среду, частично заполненную газогидратом // Инженерно-физический журнал. 2003. Т.76. №5. – С. 47-53.
6. Дмитриев В.Л., Потапов А.А. Инжекция горячего газа как энергоэффективный способ добычи газа из газогидратного месторождения // Сборник научных трудов II Всероссийской научно-технической конференции с международным участием «Высокие технологии в современной науке и технике». Т.2. – Томск: Изд-во Томского политехнического университета. 2013. – С. 365-368.

Все статьи автора «Дмитриев Владислав Леонидович»