Часть 3
3.1.Закономерность квадратичной функции y = ax2 в законе Кулона, для эквипотенциальных или равных по модулю зарядов при R const.
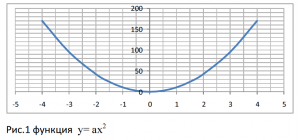
Для доказательства построим график рис. 1, F=Q2/ R2 (при равенстве Q1 = Q2, пишем Q2). R const. Значение Q берем произвольно начиная с нуля, по оси Y будем указывать силу F, по оси Х будем указывать заряд Q. Рис. 1
Мы получаем параболу, которую можно построить, используя формулу y = ax2 . Где y = F, x = Q, получаем F = аQ2 . Коэффициент а= y/ x2 или а= F/ Q 2, или а=(Q2/ R2)/ Q2 . Вставляем коэффициент а в формулу F=а Q2 получаем F=((Q2/ R2)/ Q2) Q2 производим сокращения, получаем F=Q2/ R2 . Что и требовалось доказать: закон Кулона для эквипотенциальных или равных по модулю зарядов при R const, есть не что иное, как закономерность квадратичной функции y= ax2 .
3.2 Закономерность квадратичной функции y=ax2+c, в электростатике.
Поставим опыт на весах Кулона. Подадим напряжение от высоковольтных источников напряжения на шарики, обозначим шарики как U1 и U2 .
Два источника постоянного напряжения имеют общую точку которая заземлена. Мы можем замерить напряжение относительно заземления каждого полюса, и ещё мы можем замерить напряжение полюсов относительно друг друга. И если напряжение источника А = + 8кВ. а источника В=+2 кВ., то относительно друг друга A ↔ B=6 кВ. Но источник В относительно источника А отрицателен. Что и наводит на далеко не новую мысль, что всё относительно.
Прямое соединение с источниками напряжения, шариков и заряженных плоскостей в опытах, исключает естественный разряд заряженных объектов. Отметим также, источники напряжения имеют шунтирующие сопротивление (то есть подключен как нагрузка) от 10 мОм до 20 мОм в зависимости от напряжения источника, что исключает взаимную наводку потенциалов. Это позволяет измерять силы взаимодействия, с достаточно высокой точностью.
В электростатике нет абсолютной точки (привилегированной системы отсчёта), относительно которой мы могли бы указать напряжение: За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора». За потенциальную точку отсчёта напряжения принимаем потенциал Земли (заземление), а значит и потенциал окружающего нас пространства.
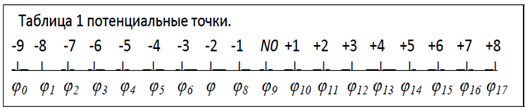
Опыт № 1: Радиусы шариков r =7,5мм, расстояние между ними R=85 мм. В начале опыта на один шарик подадим напряжение U1(6)= -3 кВ на другой U2(12)= +3кВ, разность значений потенциалов U1(6) ↔ U2(12) = φ12 –φ6= 6кВ. см. таб. 1. Затем мы будем понижать напряжение одного шарика, и повышать другого (перемещать по шкале напряжения), но сохраняя при этом разность потенциала 6 кВ, и соответственно напряженность поля Е В/м 6000 В на R 0,85 м const, между шариками .
Рассмотрим таблицу 1, верхняя шкала напряжений, точка N0=φ9N потенциал Земли (естественная потенциальная точка) относительно неё даны напряжения в кВ отрицательные и положительные, нижняя шкала потенциалов имеет нулевую точку в начале шкалы и не имеет знаков.
Поскольку потенциал (как и потенциальная энергия) может быть определён с точностью до произвольной постоянной (и все величины, которые можно измерить, а именно напряженности поля, силы, работы — не изменятся, если мы выберем эту постоянную так или по-другому), непосредственный физический смысл (по крайней мере, пока речь не идет о квантовых эффектах) имеет не сам потенциал, а разность потенциалов. ru.wikipedia.org[1]
Нам нужна разность потенциалов между потенциальными точками φ. Мы объявили нулём начало шкалы, и в этом есть определённая логика…
Заряд уединенного шара в вакууме, условно можно считать в воздухе![]() и ёмкость
и ёмкость![]() Условимся, что потенциал шарика ∆φ =φ- φ9N=U, тогда его заряд q равен
Условимся, что потенциал шарика ∆φ =φ- φ9N=U, тогда его заряд q равен ![]() . Так как силу F мы измеряем по углу отклонения в градусах, а радиусы r шариков const. То значение r и
. Так как силу F мы измеряем по углу отклонения в градусах, а радиусы r шариков const. То значение r и ![]() сводится к ролям аддитивных постоянных. Мы пишем q и
сводится к ролям аддитивных постоянных. Мы пишем q и ![]() где R расстояние между центрами шариков U1и U2.
где R расстояние между центрами шариков U1и U2.
Конечно же, здесь можно возразить, что на таком расстоянии шарики имёют взаимную ёмкость и их заряды несколько больше. Но отметим R const, а значит и взаимная ёмкость тоже const. (более подробно, смотри ниже)
Построим графическую характеристику опыта рис 2. По оси Y будем указывать угол (в градусах) на который нужно повернуть головку весов, для возвращения подвижного шарика в исходное положение, R const. По оси Х будем указывать движение условной потенциальной точки N, которая расположена ровно посередине (равноудалена)
между потенциалами U1 и U2, так для U1(8)b и U2(2)b. ![]()
То есть: U1(6)d=φ6- φ9N=-3 кВ, U2(12)d= φ12- φ9N=+3кВ, U1(6)d ↔ + U2(12)d = φ12–φ6= 6кВ, N(9)d=φ9 - φ9N =0 (потенциал земли), U1(7)с=φ7- φ9N = -2 кВ, U2(13)с= φ13 - φ9N =+4 кВ, U1(7)с ↔ U2(13)c= φ13 –φ7 = 6кВ N(10)с= φ10 -φ9N =+1 кВ.
В ходе опыта один шарик U1(9)v= φ9 -φ9N =0 (заземлён), другой U2(15)v= φ15-φ9 =+ 6кВ U1(9)v↔ U2(15)v= φ15- φ9N = 6кВ, N(12)v= φ12-φ9N =+3 кВ. и.т.д.
Здесь мы пользуемся правилом: уменьшаемое потенциальная точка, вычитаемое точка относительно которой мы указываем значение потенциала, в данном случае φ9N (потенциал земли и окружающего пространства).
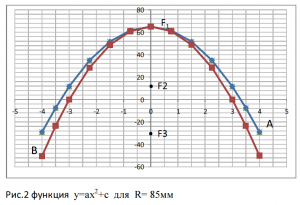
В начале построения графика отметим точку F1 для равных по модулю зарядов U1(6)d и U2(12)d, N(9)d=0. Дальше перемещая заряды по шкале напряжений, отмечаем точки по движению условной равноудаленной потенциальной точки N. Если в начале опыта точка N истинно нейтральна, входе движения становится условно нейтральной N рис. 2.
Мы получили параболу А, (парабола получена опытным путем). Теперь имея значение F1 для равных по модулю зарядов U1(6), U2(12), мы можем построить расчётную параболу, применяя формулу Кулона ![]() . В данном случае, так как R const, значение R2, мы можем заменить коэффициентом K, который находим
. В данном случае, так как R const, значение R2, мы можем заменить коэффициентом K, который находим ![]() . Также показываем параболу по движению точки N.
. Также показываем параболу по движению точки N.
Мы получили расчётную параболу В. Расчётная парабола соответствует выражению: закон Кулона работает при условии размеров заряда много меньших по сравнению с расстоянием между ними. То есть расчётная парабола не учитывает тех изменений которые возникают при расстояниях сопоставимых с размерами зарядов.
Мы также можем построить расчётную параболу, применяя квадратичную функцию y=ax2+c. Где y = F, x = N, коэффициенты с = F1, а=1 (а=1 для выражения: расстояние значительно больше размеров зарядов). Получаем F=aN2+ F1 . Мы также получаем расчётную параболу В.
Отметим, пользуясь формулой Кулона, мы умножали модули U1, U2, пользуясь квадратичной функцией мы возводим в квадрат N2 равноудалённую потенциальную точку между U1 и U2. Если силы притяжения мы принимаем за условно положительные, отталкивания за условно отрицательные, коэффициент -а со знаком минус.
Подчеркнём напряженность поля между шариками: Е В/м, 6000 В на R 0,085 м, и разность потенциалов 6000 В const. В опыте меняется только потенциалы относительно φ9N, а значит и значение зарядов относительно потенциала земли, φ9N на шкале напряжений.
Отметим также, парабола А, полученная опытом, также подчиняется закономерности квадратичной функции, из графического построения мы можем найти значения коэффициента a<1. Коэффициент а<1 и есть та закономерность которая отражает изменения с уменьшением расстояния между зарядами.
Сила F1 имеет максимальное значение при |U1|=|U2| N= 0 (равенство модулей), и убывает обратно пропорционально увеличению значения точки N (условную равноудалённую точку межу U1 и U2)
Автор утверждает заряды Q1и Q2 имеют три аргумента: напряженность поля Е относительно друг друга Е= Q1↔Q2 и напряженность поля относительно φ9N, потенциала окружающей их среды Е1= Q1↔ φ9N, Е2=Q2↔ φ9N, Е=Е1+Е2.
В современном понимании электростатики два аргумента: напряженность поля зарядов Е относительно друг друга Е1= Q1→Q2 , Е2=Q2→ Q1, Е= Q1↔Q2, Е=Е1+Е2. Вводя третий аргумент и принцип относительности, в данной работе и рассматривается электростатическое поле.
Сравним параболы полученную опытом А, и расчётом В. Как видно из графика парабола В пересекает координату Х на отметке N=3 кВ. F=0, один шарик 6 кВ другой заземлён, то есть шарики должны быть нейтральны. Парабола А показывает, что на отметке N=3 кВ. действует сила притяжения F2. Что соответствует истине, заряженные тела притягивают нейтральные.
Даётся объяснение, электризацией через влияние: пространственное распределение зарядов. Это объяснение выглядит убедительным, если нейтральное тело обладает значительным объёмом. Если же заменить шарик плоским диском из металлической фольги расположенным перпендикулярно линиям напряженности, то объяснение пространственного распределения зарядов, уже не совсем убедительно (смотри, ниже опыты с заряженными плоскостями).
Нейтральность шариков наступает, когда один шарик имеет напряжение 0.3 кВ. дугой 6,3 кВ. Для данного соотношения напряжений относительно друг друга и относительно заземления, а также расстояния между шариками и их диаметра, то есть критическое расстояние. Заметим также, что в промежутке от 0 до 0,3 кВ одного шарика и соответственно от 6 кВ. до 6,3 кВ. другого они одноимённы, но притягиваются.
Первоначально в опытах рассматривалось притяжение заряженных и нейтральных тел. Предполагалось, что как только на шарики будет подано одноименное напряжение, они начнут отталкиваться. И линия графического построения резко изменит своё движение и под прямым углом пересечёт координату Х. Было поставлено немало опытов, но линия (тогда ещё линия) не хотела пересекать координату Х перпендикулярно. Позже пришло понимание того, что это парабола и законы математики предопределяют её движение.
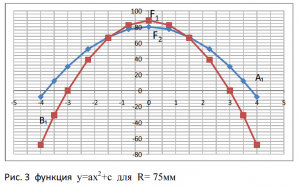
3.3. Поставим опыт № 2 аналог опыта №1 сократим только расстояние R = 75 мм. Получили параболу А1, сила F2 для равных по модулю зарядов. Рис 3. Для построения расчётной параболы В1, возьмём данные из опыта №1. Так как в начале опыта заряды равны по модулю, меняется только расстояние с R=85 мм. на R= 75 мм. Найдем коэффициент K1 для R= 75 мм. ![]() Дальше пользуясь коэффициентом K1 также показываем расчётную параболу В1, начиная с силы F1 для равных по модулю зарядов рис.3
Дальше пользуясь коэффициентом K1 также показываем расчётную параболу В1, начиная с силы F1 для равных по модулю зарядов рис.3
Из графика видно: расхождения между расчётной и опытной параболой увеличились. Силы притяжения равных по модулю зарядов меньше расчётных (более подробно для зарядов эквипотенциальных и равных по модулю, в главе гипербола в законе Кулона). С уменьшением расстояния парабола стремится к прямой линии. Чем меньше расстояние R тем больше это стремление.
Закономерность для параболы А1: здесь мы можем вычислить коэффициенты ![]() и с = F2. Заметим силу F1 следует вычислять, пользуясь классической формулой кулона
и с = F2. Заметим силу F1 следует вычислять, пользуясь классической формулой кулона ![]() , что даёт более точное значение коэффициента а.
, что даёт более точное значение коэффициента а.
Заметим вырос диапазон напряжений, в котором одноименно заряженные шарики притягиваются.
Вопрос почему это происходит. Что находится между шариками: электрическое поле. Электрическое поле создают заряженные частицы, у поля есть такая характеристика как плотность зарядов. «Плотность заряда — это количество заряда, приходящееся на единицу длины, площади или объёма, таким образом определяются линейная, поверхностная и объемная плотности заряда, которые измеряются в системе СИ: в Кулонах на метр [Кл/м], в Кулонах на квадратный метр [Кл/м²] и в Кулонах на кубический метр [Кл/м³], соответственно. В отличие от плотности вещества, плотность заряда может иметь как положительные, так и отрицательные значения, это связано с тем, что существуют положительные и отрицательные заряды.» ru.wikipedia.org [1]
То есть поле обладает зарядом QN и с уменьшением расстояния влияние заряда QN поля уменьшается, одноименные относительно поля (но не эквипотенциальные) заряды имеющие разность потенциалов относительно друг друга, притягиваются.
3.4 Поставим опыт № 3 на экранированных весах Кулона. Экранированные весы Кулона можно рассматривать как сферу: «Электрические поля от противоположных участков сферы будут точно компенсировать друг друга в любой точке внутри сферы. Оказывается и внутри замкнутой проводящей оболочки любой формы в случае выполнения закона Кулона поля не бывает. Фейнмановские лекции по физике, том 5, Глава 5» [2]
Как и в опыте №1: R 85 мм радиусы шариков 7.5мм. Подадим на шарики напряжение U1(8) = – 3 кВ и U2(12) =+ 3кВ. Напряжение шариков const, R const на всем протяжении опыта. На экран будем подавать напряжение соответствующее значению потенциалов φ5, φ6, φ8, φ9N, φ10, φ12,φ13 и.т.д. Как и в опыте № 1 мы получаем параболу А. рис 2. Опыт №3 аналогичен опыту №1. Разница лишь в том, что в опыте №1 менялись значения потенциалов шариков относительно потенциала окружающего пространства, в опыте №3 меняется потенциал окружающего пространства относительно шариков.
Наглядный пример, в чём условность деления зарядов на условно положительные и условно отрицательные. На шариках напряжение U1(8)=-3 кВ. и U2(12)=+3кВ, на экране +4 кВ или -4кВ шарики отталкиваются с силой F3. Для силы F3 соответствуют напряжения U1(8) и U2(2), N(5) или U1(10) и U2(16), N(13) рис. 2. (Если мы снимем напряжение с экрана, заземлив его, шарики снова начнут притягиваться с силой F1). Грачев В.А. Электростатическое взаимодействие зарядов в электрическом поле. Опыты на экранированных весах Кулона.[3]
Имея потенциалы -U1а = -3, +U2а = +3кВ относительно φ9N потенциала земли. Шарики отталкиваются с силой F3 в поле имеющем потенциал φ5 или φ13. То есть изменилась система отсчёта для потенциалов шариков φ13 - φ9=+4 кВ, φ5 - φ9=-4кВ.
Вернёмся к вопросу нулевого потенциала: Объявим напряжение экрана нулём, если на экране + 4 кВ обнуляем шкалу напряжений справа: N = φ13N =0, тогда U1(6)= φ6 - φ13N = - 7кВ, U 2(12)= φ12- φ13N = - 1кВ. (см. таб. № 1.)
Если на экране -4 кВ обнуляем шкалу напряжений слева N= φ5N =0, тогда U 1(6)= φ6- φ5N= +1 кВ, U 2(12)= φ12 – φ5N = + 7кВ. То есть мы получаем именно те потенциалы, которые соответствуют силе F3 (отталкивание). Отметим точка N сохраняя свой потенциал меняет свой знак, и из условно нейтральной становится истинно нейтральной.
На самом деле нулевой уровень потенциальной энергии можно выбрать где угодно. Для нас потенциальный уровень планеты земля (и окружающего её пространства) является естественной нулевой точкой N. И нужно заметить этот потенциальный уровень не отличается постоянством. Ничего страшного в такой неопределенности нет: физическим смыслом обладает не потенциальная энергия сама по себе, а разность потенциальных энергий относительно N.
К этому обязательно нужно добавить: в таком случае нулевой уровень потенциальной энергии условен, также как условно деление зарядов на условно положительные и условно отрицательные
Условному нулевому потенциальному уровню соответствует вполне вменяемая потенциальная единица, которая положительна относительно единице слева (отрицательной) , и отрицательна относительно единицы справа (положительной), т. е. нейтральна. См. таб. № 2.
Покажем это на примерах с заряженными шарами.
4.Примеры с заряженными шарами.
4.1. Возьмем два металлических шара, обозначим как О1 и О2, радиусом r1 и r2, r1 = r2. На расстоянии, значительно превосходящем их размеры. Зарядим шары одноименными потенциалами +О1(14)= φ14=+5000 В, +О2(16)= φ16=+7000 В см.таб. 1. (здесь и далее мы пишем φ14=+5000 В, подразумеваем ∆φ= φ14- φ9N=+5000B)
Заряд уединенного шара в вакууме, условно можно считать в воздухе ![]() и ёмкость
и ёмкость ![]() .Далее коэффициент пропорциональности k не показываем, мы пишем: q=φr и C= r.
.Далее коэффициент пропорциональности k не показываем, мы пишем: q=φr и C= r.
Заряды шаров относительно φ9N (потенциала земли и окружающего их пространства) q1(14)=φ14r1, и q2(16)=φ16r2 Зарядив шары мы произвели работу А1(14)= φ14q1(14), А2(16)= φ16q2(16). Потенциальная энергия заряженного шара W равна работе А, W=A, W=∆φ2r. Относительно друг друга шары О1(14)↔ О2(16) имеют разность потенциалов φ14- φ16= -2000+ В или φ16- φ14=+2000- В. Разность потециальных энергий А1-А2= Wv. А значит и разность зарядов Qv= q2(16) – q1(14) или -Qv= q1(14) – q1(16)? Всё относительно. Напишем просто 2000 В и Qv, без знака. (1)
Соединим металлической связью шары. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными. Поясним термин «равно удаленная точка» на этом примере: потенциалы и заряды шаров стали равны значению потенциала «равно удаленной точки». То есть шары стали эквипотенциальны или нейтральны друг другу.
Между шарами возникнет электрический ток, шары обменяются зарядами и соответственно энергией Wv. Переход электронов O1(14)е→ O2(16) То есть O1(14)=+5000 В отрицателен относительно O2(16) =+7000 B. (2)
Отсюда: Строго говоря, одноименныё заряды, это эквипотенциальные заряды. Каждая потенциальная единица, на шкале напряжений см таб. 1, положительна относительно единице слева (отрицательной) , и отрицательна относительно единицы справа (положительной).
При r1=r2, сложение потенциалов шаров O1+O2 , обмен энергией по формуле (3.1)равноудаленная точка:![]() Получили шары с потенциалами O1(15)=O2(15)= φ15=+6000 В, Зарядами q15= φ15r1= φ15 r2. Разрядив шар с потенциалом +O(15)= φ15 получаем работу А15= φ15q15. Работа Аz заряда шара от O1(14) до O1(15) Аz= (q15 -q1(14))(φ15-φ 14). Работа Аk разряда шара от O2(16) до O2(15) Аk= (q2(16) -q15)(φ16-φ15). Работа Аv= Wv. обмена энергией шарами О1(14) +O2(16) Аv= Аz+ Аk. Обмен зарядами Qv=(q15 -q1(14))+ (q2(16) -q15)= q16- q14.(3) Отметим один шар разряжается Аk, другой заряжается Аz. Но тем не менее, мы суммируем энергию обмена Аv= Аz+ Аk. Так как даем работу относительно равноудалённой точки φ15. Работа заряда шара O1(14) до O1(15) относительно φ9N
Получили шары с потенциалами O1(15)=O2(15)= φ15=+6000 В, Зарядами q15= φ15r1= φ15 r2. Разрядив шар с потенциалом +O(15)= φ15 получаем работу А15= φ15q15. Работа Аz заряда шара от O1(14) до O1(15) Аz= (q15 -q1(14))(φ15-φ 14). Работа Аk разряда шара от O2(16) до O2(15) Аk= (q2(16) -q15)(φ16-φ15). Работа Аv= Wv. обмена энергией шарами О1(14) +O2(16) Аv= Аz+ Аk. Обмен зарядами Qv=(q15 -q1(14))+ (q2(16) -q15)= q16- q14.(3) Отметим один шар разряжается Аk, другой заряжается Аz. Но тем не менее, мы суммируем энергию обмена Аv= Аz+ Аk. Так как даем работу относительно равноудалённой точки φ15. Работа заряда шара O1(14) до O1(15) относительно φ9N
А15- А1(14) Аz. Работа разряда шара от O2(16) до O2(15) относительно φ9N А2(16)- А15
Аk. Но (А2(16)- А15)-( А15- А1(14)) = Аz+ Аk Закон сохранения энергии q1(14)+ q2(16)= q15+ q15, q15 -q1(14)= q2(16) -q15, А1(14)+ А2(16) = А15+ А15+ Аv
(1) Как здесь видно нам уже не хватает двух знаков.
(2) Именно эта разноименность относительно друг друга сказывается на критическом расстоянии.
(3) заметим равенство (q1(15) -q14)+ (q16 –q2(1 5))= q16- q14 верно не всегда, всегда верно только для зарядов с одинаковой ёмкостью, то есть С1=С2 или r1=r2.
4.2. Возьмем два металлических шара (обозначим как О1 и О2), радиусы такие же как и в примере 4.1, r1и r2 (r1 = r2) . Зарядим шары разноимёнными потенциалами -О1(8)= φ8=-1000 В, +О2(10)= φ10=+1000В Заряды шаров -q1(8)= φ8r1, +q2 (10)=φ10 r2. Работа А1(8)= φ8 q1(8), А2(10)= φ10 q2(10). Относительно друг друга шары имеют заряд Qc=|q1(8)|+|q2(10)|. Соединим металлической связью шары. Между шарами возникнет электрический ток: -О1(8)е→ +O2(10). Работа разряда (обмена энергией) шаров Аc = А1(8)+А2(10). Сложение потенциалов при обмене энергией ![]() . Здесь мы сталкиваемся с тем , что в электростатике называется «взаимной компенсацией зарядов», автор же сводит к общему понятию: обмен энергией. Заметим разность потенциалов шаров в примере 4.1 и в примере 4.2 равенства φ14- φ16= φ8- φ10, Разность потенциалов относительно их равноудаленных точек равенства φ14- φ15=φ15-φ16=φ8-φ9=φ9-φ10. Равенство энергия обмена Аv= Аz+ Аk= Аc = А1(8)+А2(10), Аz= Аk= А1(8)=А2(10). Равенство количества зарядов Qv=(q1(15) -q14)+ (q16 –q2(15))= Qc=|q1(8)|+|q1(10)|.
. Здесь мы сталкиваемся с тем , что в электростатике называется «взаимной компенсацией зарядов», автор же сводит к общему понятию: обмен энергией. Заметим разность потенциалов шаров в примере 4.1 и в примере 4.2 равенства φ14- φ16= φ8- φ10, Разность потенциалов относительно их равноудаленных точек равенства φ14- φ15=φ15-φ16=φ8-φ9=φ9-φ10. Равенство энергия обмена Аv= Аz+ Аk= Аc = А1(8)+А2(10), Аz= Аk= А1(8)=А2(10). Равенство количества зарядов Qv=(q1(15) -q14)+ (q16 –q2(15))= Qc=|q1(8)|+|q1(10)|.
Работа обмена энергией относительно равно удалённой точки в обоих примерах равна, равно и количество зарядов которыми обменялись шары. Разница лишь в том, что в примере 4.2 равноудалённая точка истинно нейтральна, в примере 4.1 условно нейтральна (для данных потенциалов).
4.3. Рассмотрим шары с разными радиусами O1= r1 и O2= r2, ![]() Зарядим шары одноименными потенциалами О1(14)= φ14=+5000 В, О2(16)= φ16=+7000 В. Заряды шаров q1(14)= φ14 r1 , q2(16)=φ16 r2. Работа А1(14)= φ14q1(14), А2(16)= φ16 q2(16). Ёмкость шаров C1=r1, C2=r2.
Зарядим шары одноименными потенциалами О1(14)= φ14=+5000 В, О2(16)= φ16=+7000 В. Заряды шаров q1(14)= φ14 r1 , q2(16)=φ16 r2. Работа А1(14)= φ14q1(14), А2(16)= φ16 q2(16). Ёмкость шаров C1=r1, C2=r2.
Определим равноудалённую точку и заряд шаров в ней, а также заряд относительно друг друга Qw. Соединим металлической связью шары. Заряды распределятся между шарами пропорционально их ёмкости. Потенциалы шаров станут ![]() или
или ![]() заряд шара O1 станет
заряд шара O1 станет![]() заряд O2 станет
заряд O2 станет ![]() Получили шары с потенциалами +O1(14,5)=+O2(14,5)= φ14,5=5500 В, зарядами q1(14,5)=r1 φ14,5 и q2(14,5)= r2φ14,5. Потенциальной энергией А1(14,5)= q1(14,5)φ14,5 А2(14,5)= q2(14,5) φ14,5 Работа Аt заряда шара от O1(14) до O1(14,5) Аt= (q1(14,5) -q1(14))( φ14,5-φ 14) Работа Аu разряда шара от O2(16) до O2(14,5) Аu= (q2(16) –q2(14,5))(φ16- φ14,5) Работа Аw обмена энергией шарами О1(14) O2(16) Аw= Аt+ Аu Обмен зарядами Qw : здесь равенство q16- q14
Получили шары с потенциалами +O1(14,5)=+O2(14,5)= φ14,5=5500 В, зарядами q1(14,5)=r1 φ14,5 и q2(14,5)= r2φ14,5. Потенциальной энергией А1(14,5)= q1(14,5)φ14,5 А2(14,5)= q2(14,5) φ14,5 Работа Аt заряда шара от O1(14) до O1(14,5) Аt= (q1(14,5) -q1(14))( φ14,5-φ 14) Работа Аu разряда шара от O2(16) до O2(14,5) Аu= (q2(16) –q2(14,5))(φ16- φ14,5) Работа Аw обмена энергией шарами О1(14) O2(16) Аw= Аt+ Аu Обмен зарядами Qw : здесь равенство q16- q14 (q1(14,5) -q1(14))+ (q2(16) –q2(14,5)) уже не верно. Принимаем разность зарядов, равной энергетическому обмену Qw=(q1(14,5) -q1(14))+ (q2(16) –q2(14,5))
Закон сохранения энергии : q1(14)+ q2(16)= q1(14,5)+q2(14,5), q1(14,5) -q1(14)= q2(16) –q2(14,5), . А1(14)+ А2(16)= А1(14,5)+ А2(14,5)+ Аw.
4.4.Рассмотрим пример с тремя шарами. Радиусы O1= r1, O2= r2, и O3= r3, ![]()
Зарядим их разноимёнными зарядами O1= φ11=+2 кВ, О2= φ10= +1кВ, О3= φ8=-1кВ. Заряды шаров, + q1(11) = φ11r1, +q2(10) = φ10 r2, - q3(8) = φ8r3,. Работа А1(11)= φ11q1(11), А2(10)= φ10 q2(10), А3(8)= φ8 q3(8). Ёмкость шаров C1=r1, C2=r2, C3=r3.
Определим равноудалённую точку и заряд шаров в ней, заряд относительно друг друга Qm.
Потенциалы шаров в равно удаленной точки относительно φ9N: ![]() Oпределим заряды шаров в равноудалённой точке: q1(9.4)= φ9.4r1, q2(9.4)= φ9.4 r2, q3(9.4)= φ9.4 r3. Потенциальна энергия А1(9.4)= q1(9.4)φ9,4, А2(9.4)= q2(9.4) φ9.4, А3(9.4)= q3(9.4)φ9.4. Работа Аt разряда шара от O1(11) до O1(9.4) Аt= (q1(11) -q1(9.4))( φ11 -φ(9.4) ) Работа Аu разряда шара от O2(10) до O2(9.4) Аu= (q2(10) –q2(9.4))(φ10- φ9.4) Работа Аh перезаряда шара от O3(8) до O3(9.4) Аh= (|q3(8)|+q3(9.4))(|φ8|+ φ9.4)(4) Работа Аm обмена энергией шарами О3 +O2 +O1 Аm= Аt+ Аu+ Аh. Обмен зарядами Qm= (q1(11) -q1(9.4))+(q2(10) –q2(9.4))+ (|q3(8)|+q3(9.4)) Закон сохранения энергии : А1(11)+А2(10)+ А3(8) = А1(9.4) + А2(9.4) + А3(9.4) + Аm q1(11) + q2(10) - q3(8).=q1(9.4)+q2(9.4)+ q3(9.4)
Oпределим заряды шаров в равноудалённой точке: q1(9.4)= φ9.4r1, q2(9.4)= φ9.4 r2, q3(9.4)= φ9.4 r3. Потенциальна энергия А1(9.4)= q1(9.4)φ9,4, А2(9.4)= q2(9.4) φ9.4, А3(9.4)= q3(9.4)φ9.4. Работа Аt разряда шара от O1(11) до O1(9.4) Аt= (q1(11) -q1(9.4))( φ11 -φ(9.4) ) Работа Аu разряда шара от O2(10) до O2(9.4) Аu= (q2(10) –q2(9.4))(φ10- φ9.4) Работа Аh перезаряда шара от O3(8) до O3(9.4) Аh= (|q3(8)|+q3(9.4))(|φ8|+ φ9.4)(4) Работа Аm обмена энергией шарами О3 +O2 +O1 Аm= Аt+ Аu+ Аh. Обмен зарядами Qm= (q1(11) -q1(9.4))+(q2(10) –q2(9.4))+ (|q3(8)|+q3(9.4)) Закон сохранения энергии : А1(11)+А2(10)+ А3(8) = А1(9.4) + А2(9.4) + А3(9.4) + Аm q1(11) + q2(10) - q3(8).=q1(9.4)+q2(9.4)+ q3(9.4)
|q3(8)|+q3(9.4)=(q1(11) -q1(9.4))+(q2(10) –q2(9.4)) (5)
(4). Отметим, несмотря на «взаимную компенсацию зарядов», мы суммируем модули зарядов и модули потенциалов. Работа производится от и до, и нам нужна разность потенциалов и зарядов. Именно поэтому одноименные вычитаются, если с нуля начинается отсчет или он находится за пределами значений потенциалов и зарядов. И суммируется если ноль находится между значений потенциалов и зарядов.
(5) Данное равенство будет всегда, какое бы количество зарядов у вас не было: в левой части вы суммируете заряды которые были отрицательны относительно равноудалённой точки, в правой положительны относительно неё же.
4.5 Отметим уравнение 3.1, 3.2, 3.3 Мы можем решить двумя способами. Покажем это на примере 4.4:
Способ первый: даем значения потенциалов относительно φ9N ![]()
Способ второй: даём значения потенциалов относительно φ0 ![]()
5.Принцип относительности в электростатике
Представьте себе вы находитесь в изолированном от окружающей среды экранированном помещении. На экран подано напряжение скажем в 1000 000 В. отрицательное или положительное не имеет значения. Можете ли вы установить какой потенциал и знак заряда на вашем экране, не имея связи с внешним пространством? Вы ставите всевозможные эксперименты по электростатике, изучаете притяжение разноимённых и отталкивание одноимённых зарядов. Будут ли отклонения в ваших экспериментах?(6) Заметим вы ваши приборы и всё, что находится внутри экрана будут иметь потенциал экрана. Для вас и ваших приборов этот потенциал будет нулевым. Относительно этого нуля вы и будете указывать знак заряда.
Свойство частицы e, p,или n в отношении ее взаимодействия с электромагнитным полем определяются всего одним параметром – так называемым зарядом частицы Q, который в свою очередь определяется разностью потенциалов, потенциала электромагнитного поля φN и потенциала самой частицы φp φe и φn, Так если потенциал частицы меньше потенциала поля
φe< φN, то заряд Qe= (φe- φN)r=-∆φr=-Q условно отрицателен.
Если φp>φN, то Qp= (φp- φN)r=+∆φr=+Q условно положителен.
Если же потенциал поля равен потенциалу частицы . φN =φn, то Qn= (φn– φN)r=0r=0 нейтральная величина.
Нет разности потенциалов, нет заряда, но это вовсе не значит, что частица n не имеет потенциала.!
(6)Возможно если вы будете ставить опыты по электродинамике, то сила Лоренца изменит своё значение. Вопрос, какое напряжение нужно подать на экран, чтобы зафиксировать изменения
Заряженные частицы способные присоединять и делиться зарядами ( в зависимости от того положительно или отрицательно они заряжены относительно поля) стремятся к потенциалу поля, так как любая физическая система стремится к состоянию с наименьшей потенциальной энергией.
6.Притяжение одноименных зарядов
Опыт № 4 Заряженные плоскости.
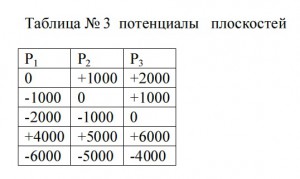
6.1Между двумя неподвижными плоскостями, обозначим как Р1 (левая)и Р3(правая), размеры которых значительно больше расстояния между ними, подвешена третья подвижная плоскость обозначим как Р2 см. фото №1. Лист фольги толщиной 0.05 мм ( при такой толщине объемное распределение зарядов сводится к нулю) наклеенный на рамку из картона, подвешен на двух проволочках. Комбинация потенциалов в вольтах, которые подавались на пластины в ходе опытов, показана в таблице 3.
Расстояние от левой плоскости Р1 до подвижной плоскости Р2 равно R1, от правой Р3 до подвижной Р2 равно R2. Со стороны левой плоскости на подвижную плоскость действует сила F1, со стороны правой F2. При равенстве расстояний R1=R2, сила F1= F2. Сократим расстояние R1: R1<R2, подвижная плоскость притягивается к левой плоскости, F1>F2. Сократим расстояние R2: R1>R2, подвижная плоскость притягивается к правой плоскости, F1< F2. В данной системе потенциалов действует только сила притяжения.
Измерение силы притяжения (угол отклонения плоскости Р2), показывает, во всех случаях она одинакова. То есть имеет значение только разность потенциалов, одноименность или разноимённость, а также нейтральность одного из потенциалов не имеет значения для сил притяжения, в данной системе.
Отметим сила отталкивания возникает в этой системе, если на подвижную плоскость Р2 подать потенциал равный одной из плоскости или выходящий за пределы потенциалов плоскостей Р1 и Р3 . Но это уже опыты Милликена и Иоффе.
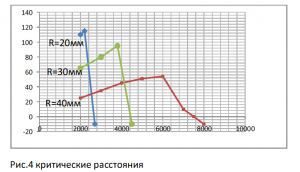
6.2 Опыт №5. Шарики диаметром 15мм, расстояние между шариками R=40мм.(затем повторим опыт для R=30мм и R=20мм). Подадим эквипотенциальное напряжение U 1= + 2кВ и U 2= +2 кВ. на шарики. Поворачивая головку весов, скомпенсируем силу отталкивания и вернём шарик в исходную точку (расстояние r между шариками 40 мм. r const).
Построим график рис.4, по оси Х мы будем показывать напряжение шарика в Вольтах, номинал которого будет меняться в ходе опыта, по оси Y силу F в градусах. Отметим на графике силу F1 для эквипотенциального напряжения U1= + 2кВ и U2= +2 кВ. Дальше мы будем поднимать напряжение первого шарика U1, второй же будет под напряжением U2=+2кВ, на всём протяжении опыта.
Как видно из графика сначала сила отталкивания растёт почти по прямой. Затем снижает свой рост и в районе 6 кВ падает. При соотношении напряжений + 2 кВ одного и +7 кВ другого сила отталкивания составляет 10 градусов, +2 кВ и +7.5 кВ 0 градусов : нейтральное состояние. А при соотношении +2 кВ и +8кВ. шарики притягиваются силой 10 градусов. Для расстояния R=30мм шарики начинают притягиваться при соотношении напряжений 2 кВ и 4,3 кВ, для R= 20мм соотношение напряжений 2 кВ и 2,5 кВ.
Одноименные заряды, но не эквипотенциальные, одноименны относительно поля. Но относительно друг друга имеют разность потенциалов, и могут рассматриваться как разноименные. Что и было доказано в ходе опыта.
Одноименные, но не эквипотенциальные заряды, испытывают две силы притяжение и отталкивания. И на определённом расстоянии между ними, эти силы находятся в равновесии: нейтральном состоянии. И если мы увеличим это расстояние (не меняя напряжение шариков), они снова начнут отталкиваться, и соответственно уменьшив, притягиваться. Баланс сил и определяет взаимодействие.
7.Гипербола в электростатике.
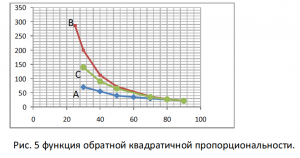
То, что закон Кулона имеет функцию обратной квадратичной пропорциональности для эквипотенциальных или равных по модулю зарядов при Q1 =Q2 const, в доказательстве не нуждается.
Все опыты ставятся так, что бы менялось, что то одно. Что как видно это вполне оправдано. Вот и в данном опыте меняться будет только одно расстояние R. Шарики эквипотенциальны или равны по модулю 2 кВ. Меняем только расстояние. По оси Y сила в градусах по оси Х расстояние между шариками в миллиметрах. Мы получили две гиперболы А для одноименных, С разноименных, и гипербола В расчётная. Рис 5
Как видно с уменьшением расстояния силы взаимодействия отличаются от расчетных, в меньшую сторону. Одноименные 700 , разноимённые 1400 и расчетные 2000 для расстояния 30мм. Здесь можно только повторить с уменьшением расстояния, заряд поля, обозначим как а, уменьшается. Для одноименных эквипотенциальных, это имеет большее значение, так как относительно друг друга разность потенциалов равна нулю, а значит они не имеют взаимной ёмкости. Функция обратной квадратичной пропорциональности здесь y=c/x2 где y=F х=R c=Q2а
Какое объяснение здесь можно дать? В опытах меняется расстояние, прямо пропорционально уменьшению расстояния, уменьшается в коэффициенте с значение третьего аргумента : а заряд поля.
Библиографический список
- Электрическоеполе [Электронныйресурс].URL:http://ru.wikipedia.org/
- Фейнмановские лекции по физике http://www.all-fizika.com/article/index.php
- Грачев В.А. Электростатическое взаимодействие зарядов в электрическом поле. // Исследования в области естественных наук. – № 7 Июль 2013 [Электронный ресурс]. URL: http://science.snauka.ru/2013/07/5289