В настоящее время все более актуальной становится проблема выбора объекта из множества конкурирующих: выбор управляющего алгоритма, выбор технического решения или устройства, государственные закупки и.т.д. В последнее время для решения данных вопросов привлекаются эксперты. Для математической обработки результатов экспертных заключений, в частности, можно использовать коэффициент конкордации [1,с.42].
Экспертам ( m человек) предлагается анкета с описанием объектов. Заполняя анкету j –й (j=1,2,…,m) специалист назначает i-му (i=1,2,…,к) объекту ранг 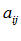 . Если j –й эксперт не может указать порядок следования для
. Если j –й эксперт не может указать порядок следования для 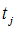 рядом стоящих объектов, начиная с
рядом стоящих объектов, начиная с 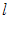 -го, то объектам приписывается один и тот же ранг:
-го, то объектам приписывается один и тот же ранг:
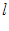 +
+ 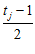 .
.
Если эксперт не может разграничить Q групп членов ряда, содержащих каждая 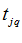 (q = 1,2,…,Q) объектов, и группы начинаются соответственно с
(q = 1,2,…,Q) объектов, и группы начинаются соответственно с 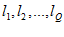 – го члена ряда, всем
– го члена ряда, всем 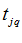 членам q – й группы приписывается ранг
членам q – й группы приписывается ранг
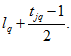
Далее подсчитываются:
1. Сумма рангов 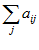 ;
;
2. Разность между суммой и средней суммой рангов
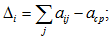
3. 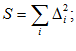
4. Коэффициент конкордации
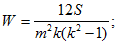
Если W = 0 – отсутствует согласия во мнениях экспертов по выбору объекта, W=1 – полное согласие опрошенных. Величина 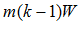 имеет
имеет 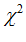 – распределение с числом степеней свободы к – 1 . Тогда значимость коэффициента проверяем по критерию
– распределение с числом степеней свободы к – 1 . Тогда значимость коэффициента проверяем по критерию 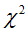 . Подсчитываем расчетное
. Подсчитываем расчетное
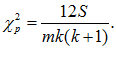
Сравниваем расчетное значение с табличным 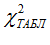 при заданном уровне значимости
при заданном уровне значимости 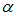 и числе степеней свободы k-1. Гипотеза о наличии согласия не отвергается если
и числе степеней свободы k-1. Гипотеза о наличии согласия не отвергается если 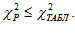 . Если коэффициент конкордации незначим, то это означает отсутствия согласия во мнениях о выборе объекта. Это может случиться, когда недостаточно информации.
. Если коэффициент конкордации незначим, то это означает отсутствия согласия во мнениях о выборе объекта. Это может случиться, когда недостаточно информации.
Дополнительная информация может быть представлена кортежем показателей эффективности каждого объекта. Одни показатели из кортежа могут быть подсчитаны достаточно просто, другие – требуют имитационного моделирования с привлечением процедур векторной оптимизации. Данные процедуры и эксперты образуют, своего рода, контур автоматизированного принятия решения, где экспертам дается подсказка или рекомендация: принять объект (группу объектов) или отвергнуть.
Предлагая экспертам, последовательно, значения показателей из данного кортежа приведет, видимо, к переоценке рангов и процедура расчета коэффициента конкордации повторяется в цикле.
Можно предположить, что наличие в процедурах на каждом шаге реакции экспертов, изменяет вероятность принятия правильных решений, т.е. уменьшает или увеличивает степень неопределенности. За меру неопределенности можно взять энтропию опыта [2,с.38].
Пусть m –множество конкурирующих алгоритмов работы объекта или множество объектов. Если нет информации относительно объектов, то выбор равновероятен 1/m.
Опыт О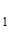 : выбор объекта, у экспертов нет предварительной информации. Энтропия опыта
: выбор объекта, у экспертов нет предварительной информации. Энтропия опыта
Н (О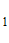 ) =
) = 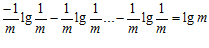 (m -слагаемых).
(m -слагаемых).
Опыт О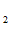 : получена информация для экспертов, отобраны m
: получена информация для экспертов, отобраны m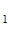 из множества m. Исходы опыта О
из множества m. Исходы опыта О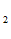 : О
: О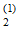 - коэффициент W значим; О
- коэффициент W значим; О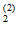 – коэффициент W незначим. Вероятности исходов
– коэффициент W незначим. Вероятности исходов
Р (О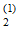 )= m
)= m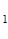 /m , Р(О
/m , Р(О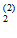 )=(m- m
)=(m- m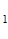 )/m. Энтропия опыта
)/m. Энтропия опыта
Н (О )=
)=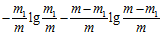 .
.
Далее эксперты отбрасывают m из m (пусть m
из m (пусть m
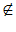 m
m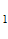 ).
).
Опыт О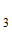 : исходы О
: исходы О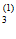 - коэффициент W значим; О
- коэффициент W значим; О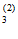 - коэффициент W незначим. Условные вероятности
- коэффициент W незначим. Условные вероятности
Р(О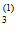 / О
/ О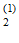 )=
)=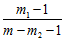 ; Р(О
; Р(О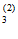 / О
/ О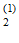 )=
)=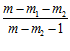 ;
;
Р(О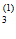 / О
/ О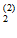 )=
)=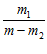 ; Р(О
; Р(О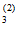 / О
/ О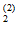 )=
)=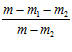 . Тогда
. Тогда
Н(О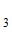 / О
/ О ) = -
) = -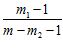 lg
lg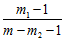 –
– 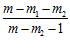 lg
lg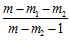 ;
;
Н(О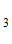 / О
/ О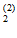 ) = –
) = – 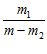 lg
lg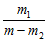 –
– 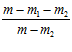 lg
lg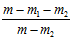 .
.
Н(О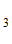 / О
/ О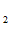 ) = Р(О
) = Р(О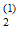 ) Н(О
) Н(О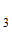 / О
/ О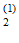 ) + Р(О
) + Р(О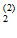 ) Н(О
) Н(О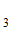 / О
/ О )=
)=
= 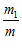 [-
[-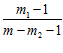 lg
lg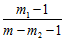 -
- 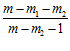 lg
lg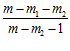 ] +
] +
+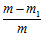 [-
[-  lg
lg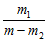 -
- 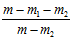 lg
lg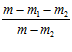 ].
].
Пусть m =10, m = m
= m =2. Тогда Н(О
=2. Тогда Н(О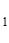 )=1-полная неопределенность, Н(О
)=1-полная неопределенность, Н(О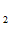 )=0,1768, Н(О
)=0,1768, Н(О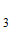 / О
/ О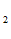 ) =0,1274.
) =0,1274.
Как видно из примера, включение экспертов в контур автоматизированного принятия решений, уменьшает энтропию или степень неопределенности. В дальнейшем представляет интерес увеличения числа опытов до четырех или пяти, и проанализировать энтропию для различных исходных данных.
Библиографический список
- Зедгинидзе И.Г. Планирование эксперимента для исследования многокомпонентных систем. М.: Наука,1976.-377с.
- Яглом А.М., Яглом И.М. Вероятность и информация. М: Наука,1973.-506 с.


