Математическое моделирование активно применяется при поддержке поиска эффективных решений сложных проблем, в том числе проблем оптимального выбора. В процессе анализа математических моделей важную роль играют многокритериальные методы оптимизации, позволяющие учесть противоречивые требования, предъявляемые к приобретаемому товару. В рамках многокритериальных методов важную роль играют множество решений, эффективных по Парето. Выбор чего-либо, с учетом различных критериев, является сложной задачей планирования и принятия решения [1].

Объектом изучения является необходимость покупки внешнего жёсткого диска.

Применению критерия Парето уделяется немало внимания. Изучением и применением метода Парето занимаются многие российские и зарубежные учёные. В.Ф.Шуршев и Л.В.Буй [2] рассмотрели алгоритм рационального выбора сканирующих приемников и трансиверов на основе использования критерия Парето. Ю.В.Кандырин и др. исследовали математические модели структурирования альтернатив для решения задач выбора в САПР [3]. Е.М.Гальцов и А.В.Гавриленко [4] предлагают использовать Парето-оптимальные решения для прогнозирования по критерию эффективность-стоимость тактико-технико-экономических характеристик рекомендуемых к созданию РЛС воздушно-космической обороны. Ю.А.Заргарян [5] уделил внимание ранжированию критериев экспертами с применением бинарных (в общем случае нечетких) отношений. После окончания ранжирования появляется задача принятия решений на основе многокритериального выбора. В своей работе G.Debdas и C.Debjani [6] предлагают новый метод решения многокритериальных задач, и объясняют как добиться оптимальных показателей решения по Парето. В статье K.Fujiwara[7] рассматривается процесс экономических издержек, предложен способ решения данной проблемы с помощью критерия Парето. F.Mastroddi, S.Gemma [8], используя Парето, проводят многопрофильный анализ конструкции самолёта. X-B.Hua, M.Wanga, Q.Yea, Z.Hanb, M.S.Leesonc [9] решают вопрос оптимального распределения ресурсов между проектами разработки новых продуктов, решение обеспечивается методами Парето. A.Y.Golubin [10] описывает способ применения Парето-оптимальных решений в случае двумерного пространства полезности. Р.И.Баженов и др. [11-21] исследовали и применяли многокритериальные методы выбора решений.

Для исследования был проведён анализ предложений в Интернет-магазинах и отобрано шесть внешних жёстких диска:
1. Внешний HDD-накопитель Sony HD-E1
2. Внешний HDD-накопитель Silicon Power Diamond D20
3. Внешний HDD-накопитель Seagate Expansion STBX1000201
4. Внешний HDD-накопитель Hitachi HTOLMX3EA10001ABB
5. Внешний HDD-накопитель A-Data ANH13-1TU3-CBK
6. Внешний HDD-накопитель 3QHDD-T225-EB1000
Отметим, что интерфейс подключения (USB 3.0) и объём (1 Tb) у всех дисков одинаков, поэтому в сравнениях данные характеристики не участвуют.
Характеристики отобранных внешних жёстких дисков, участвующие в сравнении приведены в табл. 1. В заголовках показателей указана направленность:  − направленность на максимум,  − направленность на минимум.
Таблица 1 – Основные характеристики внешних жёстких дисков

Устройство	Показатель
	e1 - Цена (руб.)	e2 - Вес (г.)	e3 - Скорость вращения диска (rpm.)	e4 - Скорость передачи данных (Гб/с)
a1,  Sony HD-E1	4490	230	7200	5
a2,  Silicon Power Diamond D20	4490	135	5400	0,5
a3,  Seagate Expansion STBX1000201	4590	170	5400	5
a4,  Hitachi HTOLMX3EA10001ABB	4390	240	5400	5
a5,  A-Data ANH13-1TU3-CBK	4890	165	5400	5
a6,  3QHDD-T225-EB1000	4590	235	5400	5

Полученное множество альтернатив состоит из n элементов. Такое множество альтернатив обозначим, как А={a_i}, i=  где a_i - альтернативы, полученные при выборе жестких дисков; a={e_j},j=где e_j - показатели качества а. Показатели качества {e_j}, j= вариантов A={a_i} описываются их значениями {e_i,j} по строкам.

Алгоритм выбора оптимальных альтернатив по критерию Парето начинается с составления ассоциативных матриц АМ_j [2]. Приведем описание метода.

В основу алгоритма выбора по критериям Парето положена модель описания множеств возможных вариантов с помощью фактор-множества F(A/e), которым являются множества окрестностей единичного радиуса, взятых для всех a_i  A, i=. 

Окрестность O_i элемента a_i представляет собой множество элементов {a_i*}, доминирующих или эквивалентных a_i (a_i*>=a_i).

Линейные порядки альтернатив требуется построить в виде реляционного отношения

L(A/e_j)=<a_i+1, a_i, …, a_n>, i=, a_i+1a_i по e_j, j=.

Если альтернатива a_i доминирует альтернативу a_k, то элемент ассоциативной матрицы d^j_i,k= 1, иначе d^j_i,k= 0. Если альтернативы a_i, a_k несравнимы по данному показателю качества, то элементы d^j_i,k = d^j_k,i =1. Элементы главной диагонали всегда принимают значение равное 0 [2]. Таким образом, 

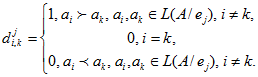
Осуществим построение ассоциативных матриц (табл. 2-5). Для нахождения элементов покажем найденные в результате анализа табл. 1 линейные порядки по e₁, e₂, e₃, e₄:
L(а/e₁)= {{а₁, а₂}, {а₃, а₆},{ а₄}, {а₅}};
L(а/e₂)= {{а₁}, {а₂}, {а₃}, {а₄}, {а₅}, {а₆}};
L(а/e₃)= {{а₁}, {а₂, а₃, а₄, а₅, а₆}};
L(а/e₄)= {а₁, а₃, а₄, а₅, а₆}, {а₂}

Таблица 2 – АсМ₁

Таблица 3 – АсМ₂

Таблица 4 – АсМ₃

Таблица 5 – АсМ₄

На основе ассоциативных матриц АсМ₁, АсМ₂, АсМ₃, АсМ₄ путем пересечения фактор-множеств по каждому из показателей качества строим результирующую матрицу АсМ_рез (табл.6).

Таблица 6 – Результирующая ассоциативная матрица АсМ_рез

По критерию Парето альтернатива а_h включается во множество оптимальных вариантов, если значение Z_h=c_1,h  c_2,h  …  c_n,h=0. Из табл.6 видно, что результирующая ассоциативная матрица содержит окрестности O₁(а₁), O₃(а₃), O₆(а₆), у которых значения Z₁, Z₃, Z₆=0 соответственно. Следовательно, а_1, а_3, а₆ являются наихудшими вариантами исходного множества. 

По данным табл. 6 результирующая ассоциативная матрица содержит окрестность O₁(а₁), O₂(а₂) и O₄(а₄), у которой значения Z₁,Z₂,Z₄=0 соответственно. Таким образом, а_1, а_2, а₄ – наихудшие варианты исходного множества.

Произведем удаление найденных наихудших вариантов в результирующей матрице (табл.7).

Таблица 7 – Матрица после удаления альтернатив а_1,а_2,а₄

Аналогично удалим наихудшие варианты (табл.8).

Таблица 8 - Матрица после удаления альтернативы а₃

Продолжаем удалять наихудшие варианты (табл.9).

Таблица 9 – Матрица после удаления альтернативы а₆

После произведенных операций получен следующий порядок (а₁, а₂, а₄) (а₃) (а₆) а₅.

В результате исследования мы выяснили, что внешний жёсткий диск №5 (HDD-накопитель A-Data ANH13-1TU3-CBK) является наиболее оптимальным вариантом по критерию Парето.

1. Лотов А.В., Поспелова И.И. Многокритериальные задачи принятия решений: Учебное пособие. М.: Макс Пресс, 2008. 197 с.
2. Шуршев В.Ф., Буй Л.В. Использование критерия Парето при рациональном выборе сканирующих приемников и трансиверов // Вестник Астраханского Государственного Технического Университета. Серия: управление, вычислительная техника и информатика. 2014. №1. С. 112-120.
3. Кандырин Ю.В., Сазанова Л.Т., Шкурина Г.Л. Математические модели структурирования альтернатив для решения задач выбора в САПР // Известия Волгоградского государственного технического университета. 2011. Т. 3. № 10. С. 111-115.
4. Гальцов Е.М., Гавриленко А.В. применение Парето-оптимальных решений при тактико-технико-экономическом обосновании многофункциональных РЛС воздушно-космической обороны // Вооружение и экономика. 2013. № 2(23). С. 3-13.
5. Заргарян Ю.А. Ранжирование критериев для Парето-оптимальных решений многокритериальных задач // Известия Южного федерального университета. Технические науки. 2012. №2(127). С. 153-159.
6. Debdas G., Debjani C. A new Pareto set generating method for multi-criteria optimization problems // Operations Research Letters. 2014. №42. С. 514–521.
7. Fujiwara K. Pareto-improving tariff-tax reforms under imperfect competition // International Review of Economics & Finance. 2014. №31. С. 12–20.
8. Mastroddi F., Gemma S. Analysis of Pareto frontiers for multidisciplinary design optimization of aircraft // Aerospace Science and Technology. 2013. №28. С. 40–55.
9. Hua X-B., Wanga M., Yea Q., Hanb Z., M. S. Leesonc Multi-objective new product development by complete Pareto front and ripple-spreading algorithm  // Neurocomputing. 2014. №142. С. 4–15.
10. Golubin A.Y. On Pareto optimality conditions in the case of two-dimension non-convex utility space // Operations Research Letters. 2013. №41. С. 636–638.
11. Винокуров А.С., Баженов Р.И. Использование метода анализа иерархий для принятия оптимального решения по выбору цифрового фотоаппарата // Современная техника и технологии. 2014. № 9 (37). С. 11-17.
12. Винокуров А.С., Белов И.В., Баженов Р.И. Использование критерия Парето для принятия оптимального решения по выбору цифрового фотоаппарата // Современная техника и технологии. 2014. № 10 (38). С. 36-41.
13. Винокуров А.С., Белов И.В., Баженов Р.И. Использование метода нечёткого отношения предпочтения для принятия оптимального решения по выбору цифрового фотоаппарата // Современная техника и технологии. 2014. № 11 (39). С. 37-44.
14. Кардаш А.С., Манойленко И.Г., Баженов Р.И. Принятие Парето-оптимального решения для выбора планшетного компьютера // Исследования в области естественных наук. 2014. № 11 (35). С. 41-46.
15. Кардаш А.С., Винс А.А., Баженов Р.И. Об оптимальном выборе планшетного компьютера для младшего школьника // Современная техника и технологии. 2014. № 10 (38). С. 69-75.
16. Приходько Е.А., Баженов Р.И. Применение системы mpriority для оптимального выбора программы, решающей проблемы автоматизации документооборота // Nauka-Rastudent.ru. 2014. № 10 (10). С. 29.
17. Баженов Р. И. Информационная безопасность и защита информации: практикум. Биробиджан: Изд-во ГОУВПО «ДВГСГА», 2011. 140 с.
18. Наумов А.А., Баженов Р.И. О неустойчивости метода нормализации критериев // Современные научные исследования и инновации. 2014. № 11-1 (43). С. 64-68.
19. Баженов Р.И. О методике обучения проектированию информационных систем будущих менеджеров // Психология, социология и педагогика. 2014. № 8 (35). С. 30-38.
20. Баженов Р.И. Об организации научно-исследовательской практики магистрантов направления «Информационные системы и технологии» // Современные научные исследования и инновации. 2014. № 9-2 (41). С. 62-69.
21. Vexler V.A.,BazhenovR.I., Bazhenova N.G. Entity-Relationship Model of Adult Education in Regional Extended Education System // Asian Social Science. 2014. Т. 10. №20. С.1-14.

Все статьи автора «Баженов Руслан Иванович»