В работе А.В. Баяндина «К распределению простых чисел в натуральном ряде» [1] джоинт-рядом чисел фактически называется матрица: Xin=Ji+3n, где Ji – одно из 8 порождающих чисел: 1,7,11,13,17,19,23,29; n=0,1,3… – номер строки, i – номер столбца.
Так как единица по мнению автора выполняет функцию нуля, то первый период джоинт-ряда начинается с 7, и заканчивается 31. Это изменение позволяет записать рядом числа-близнецы: 29-31, 59-61 и т.д.
Первым столбцом в этой матрице становится прогрессия по порождающему числу 7: X7=7+30n, X=7,37,67,…,187,217,247, последние три числа в этой записи являются составными, поэтому они записаны как 11х17, 7х31, 13х19.
Мы считаем, что данная типология числа заслуживает внимание, так как она привязана к десятичной системе счисления. В ней проявляется классификация простых чисел вида p=6k+1, при делении на 6 имеющие остаток 1, которые, как доказал Пьер Ферма, имеют разложение в неполные квадраты суммы и разности p1,2=m2+n2±mn, и в сумму трех квадратов p3=m2+3n2. 7=2∙2+1∙1+2∙1=3∙3+1∙1+3∙1=2∙2+3∙1∙1.
Нашим изобретением стало комплексное представление этого числа в конфигурации правильного треугольника, в котором выделяются треугольники и трапеции:
1)наибольшей целочисленной стороны тупоугольного треугольника с углом 120о.
2)длиной средней стороны остроугольного треугольника с углом 60о.
Эти два представления объединяются в равнобедренной трапеции, вписанной в правильный треугольник. Причем оказывается, что существует две таких трапеции и два остроугольных треугольника (рис.1).
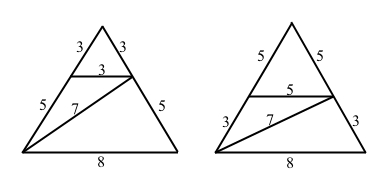
Рисунок 1 – Представление простого числа в конфигурации правильного треугольника
Завершающим этапом становится проверка формулы Л.Эйлера для вписанного в окружность четырехугольника: сумма квадратов четырех сторон равна сумме квадратов диагоналей плюс учетверенный квадрат разности отрезка, соединяющего середины диагоналей.
Проверку можно осуществить и при помощи формулы Клавдия Птоломея: Сумма произведения противоположных сторон вписанного в окружность четырехугольника равна произведению длин диагоналей.
В математике пифагоровых триад первым простым числом является число 5, которое разлагается в сумму двух квадратов разной четности.
На основе прямоугольных и тупоугольных треугольников с углом 120о, составлена таблица простых чисел с периодом T=24. Этот период определяется из объединения Рождественских теорем Ферма для простых чисел: p=4k+1; p=8k+1; p=8k+3; p=6k+1, когда простые числа разлагаются соответственно в сумму двух, трех и четырех квадратов. Из этих разложений строятся триады прямоугольных, тупоугольных, остроугольных треугольников с углами 120о ,60о,45o,135oи четверки прямоугольных параллелепипедов. Так как периоды в арифметических прогрессиях 4,6,8 то общий период в квазипериодической таблице простых чисел равен 24. Таким образом, мы получили:
первый столбец определяет простые числа вида 5+24∙k {4k+1; 6k+1; 8k+7} – красн.,
второй столбец – 7+24·k: {4k+3; 6k+1; 8k+7} – зеленые цифры,
третий – 11+24k: {4k+3; 6k+5; 8k+3} – синие цифры,
четвертый – 13+24k: {4k+1; 6k+1; 8k+5} – красные и зеленые цифры,
пятый – 17+24k: {4k+1; 6k+5; 8k+1} – оранжевые цифры,
шестой – 19+24k: {4k+3; 6k+1; 8k+3} – зеленые и оранжевые цифры,
седьмой – 23+24k: {4k+3; 6k+5; 8k+7} – фиолетовые цифры,
восьмой – 73+24k: {4k+1; 6k+1; 8k+1} – оранжевые и зеленые цифры.
В первой и во второй строке матрицы мы получаем также и составные числа 25 и 49 , которые как и простые числа разлагаются в сумму двух квадратов.
В пределах первой сотни мы выделяем в прямоугольные треугольники, для которых значения углов измеряются на транспортире. В нашей таблице теорема Пифагора выражена формулой прямоугольника с длинами сторон и диагоналей напр.: 12x35.37. Два знака «x» определяет прямоугольный параллелепипед, у которого три измерения и длина диагонали целые числа напр.: 11x6x6.11. Запись 3,8,7; 60о обозначает треугольник со сторонами 3,8,7 и углом 60о.
Тр. 1,3,3,2 – трапеция с основаниями равными 1, 2 и боковыми сторонами длиной 3.
Таблица 1 – 8 Web-матрица геометрических представлений простых и ассоциированных с ними составных чисел джоинт-ряда
| I
4k+1 m2+n2 6k+5 8k+5
|
II
4k+3 6k+1 m2+n2+mn 8k+7
|
III
4k+3 6k+5 8k+3 m2+2n2 |
ІV
4k+1 m2+n2 6k+1 m2+n2+mn 8k+5
|
V
4k+1 m2+n2 8k+1 m2+2n2 6k+5 |
VI
4k+3 6k+1 m2+n2+mn 8k+3 m2+2n2 |
VII
4k+3 6k+5 8k+7 m2+2n2+22 m2+n2+k2+l2
|
VIII
4k+1 m2+n2 6k+1 m2+n2+mn 8k+1 m2+2n2 |
| 3x4.5; 36,9o
5 22+12 1,3√2,5;135o 1x2x2.3; 19,5o
|
7 22+12+2∙1 3,8,7;60o 5,8,7;60o 3,5,7;120o 2х3х6.7 тр. 3,5,3,8 тр. 5,3,5,8
|
11 32+2·12 2х6х9.11 7x6x6.11
|
5x12.13;22,6o
13 32+22 32+12+3∙1 17,5√2,13;45о 7,12√2,13;45о 17,12√2,13;45о 7,5√2,13;45o 7,15,13;60o 8,15,13;60o 7,8,13;120o 3х4х12.13 |
8×15.17; 28o4’
17 42+12 32+2·22 23,8√2,17;45o 7,15√2,17;45o 23,15√2,13;45o 1x4x8.9; 1x12x12.17
|
19 32+22+3∙2 12+2∙32 5,21,19;60o 16,21,19;60o 5,16,19;120o 1х6х18.19 6x6x17.19 6х10х15.19 |
23 12+2∙32+22 тр.1,3,3,2 3х6х22.23 3х14х18.23 6х13х18.23
|
7x24.25;16,3o
25=52 31,7√2,25;45o 17,24√2,25;45o 31,24√2,25;45o 17,7√2,25;135o 9х12х20.25 12х15х16.25
|
| 20x21.29;43,6o
29 52+22 41,20√2,29;45o 1,21√2,29;45o 41,21√2,29;45o 1,20√2,29;135o 3х16х24.29 11х12х24.29 12х16х21.29 |
31 52+12+5∙1 11,35,31;60o 24,35,31;60o 11,24,31;120o 5х6х30.31 5х8х30.31 6х14х27.31 6х21х22.31 14х18х21.31
|
35=5∙7 6х10х33.35 6х17х30.35 15х18х26.35 |
12x35.37;18,9o
37 62+12 42+32+4∙3 47,12√2,37;45o 23,35√2,37;45o 47,35√2,37;45o 7,40,37;60o 33,40,37;60o 7,33,37;120o 23,12√2,37;135o 3х24х28.37 8х24х27.37 12х21х28.37 |
9x40.41; 12,6o
41 52+42 32+2∙42 49,9√2,41;45o 31,40√2,41;45o 49,40√2,41;45o 31,9√2,41;135o 4х12х39.41 4х24х33.41 9х24х32.41 12х24х31.41 |
43 62+12+6∙1 52+2∙32 13,48,43;60o 35,48,43;60o 13,35,43;120o 2х18х39.43 6х7х42.43 7x30x30.43 9х18х38.43 18х25х30.43 |
47 52+2∙32+22 тр.5,3,3,2 16,47√2,65;135 2х21х42.47 6х18х43.47 6х27х38.47 11х18х42.47 18х21х38.47 18х27х34.47 |
49=72 16,55,49;60o 39,55,49;60o 16,39,49;120o 16,23,49;120o 4х9х48.49 9х32х36.49 12х24х41.49 12х26х36.49 14х21х42.49 15х24х40.49 |
| 28x45.53;31,9o
53 72+22 73,28√2,53;45o 17,45√2,53;45o 73,45√2,53;45o 17,28√2,53;135o 8х21х48.53 12х19х48.53 12х27х44.53 |
55=5∙11 3х30х46.55 6х35х42.55 18х26х45.55 19х30х42.55 |
59
32+2∙52 6х41х42.59 9х30х50.59 14х39х42.59 |
11x60.61;10,4o
61 62+52 52+42+5∙4 71,11√2,61;45о 49,60√2,61;45о 71,60√2,61;45о 49,11√2,61;135o 9,65,61;60o 56,65,61;60o 9,56,61;120o 11х36х48.61 |
16x63.65;14,3o
33x56.65;30,9o 39x52.65 65=5∙13 79,16√2,65;45o 89,33√2,65;45o 23,56√2,65;45o 89,56√2,65;45o 47,63√2,65;45o 79,63√2,65;45o 47,16√2,65;45o |
67
72+22+7∙2 72+2·32 32,77,67;60o 45,77,67;60o 32,45,67;120o 15х42х50.67 18х42х49.67 |
71
72+2·32+22 62+52+32+12 тр.7,3,3,2
|
48x55.73;41,1o
73 82+32 82+12+8∙1 12+2∙62 7,55√2,73;45o 17,80,73;60о 63,80,73;60о 17,63,73;120о 7,48√2,73;135o |
| 36×77.85
77=7∙11
|
79
72+32+7∙3 40,91,79;60o 51,91,79;60o 40,51,79;120o |
83
92+2∙12 |
13×84.85;8,8o
36×77.85;25o 51×68.85 85=5∙17 97,13√2,85;45o 17,68√2,85;45o 71,13√2,85;135o 41,36√2,85;135o |
39×80.89;26o
89 82+52 92+2∙12 41,39√2,89;135o |
35×84.91
91=7∙13 11,96,91;60o 19,99,91;60o 80,99,91;60o 85,96,91;60o 11,85,91;120o 19,80,91;120o |
57×76.95
95=5∙19
|
65×72.97;42,1o
97 92+42 82+32+8∙3 52+2∙62 55,57,97;120o 7,65√2,97;135o
|
Библиографический список
- А.В.Баяндин. К распределению простых чисел в натуральном ряде чисел. «НАУКА», Новосибирск, СИФ РАН, с. – 40, 1999.
- А.Правдин. Составляем упражнения по математике// Математика (приложение к газете «1 сентября»), №7, 1997.
- Эрдниев Б.П. Матрицы в обучении. – Калмыцкий университет; 1990.
- Горяев В.М. Матрица как средство уплотнения, систематизации, углубления и упорядочивания учебного материала в контексте единого учебника математики//Этнос. Образование. Личность: Тез. доклада научно-практической конференции. Якутск: ЯИУУ, 2005. с.101-103.
