В данной статье рассматриваются свойства так называемых специальных и р-специальных групп, введенных и изучаемых автором в работах [1] и [4]. Необходимые определения и обозначения приведены в работах [1] – [8].

ОПРЕДЕЛЕНИЕ 1. Пусть А и B – рациональные группы. Упорядоченную пару элементов (α, β), где 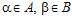, будем называть базисом подпрямой суммы G групп А и В, если G_А = <α>, G_В = <β>.

ОПРЕДЕЛЕНИЕ 2. Пусть р – простое число. Абелеву группу без кручения G ранга 2, будем называть р-специальной, если

1) группа G является подпрямой суммой рациональных групп, изоморфных рациональной группе Q ^р;

2) группа G обладает базисом.

Пусть далее, для некоторых делимых рациональных групп А и B, G – специальная группа с базисом (α, β)  – подгруппа  прямой суммы групп А и В, Z – кольцо целых чисел. Для любого простого числа р, через G ^р будем обозначать множество пар  вида 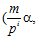 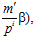 где i = 0, 1, 2, … ; т, m′  – целые числа, взаимно простые с числом р.

ЛЕММА 1. Множество G ^р образует подгруппу группы G.

Доказательство. Данное утверждение следует из очевидной замкнутости множества G ^р относительно операции сложения.

ОПРЕДЕЛЕНИЕ. Пусть  A′ и B′ – рациональные группы, изоморфные группе Q ^р, для некоторого простого числа р, подгруппу прямой суммы групп A′ и B′ будем называть р-специальной, если она является подпрямой суммой групп A′ и B′, индуцированной группой Q ^р/Z, с базисом (α, β).

Введем следующее обозначение: если А и B – делимые рациональные группы и G – специальная группа с базисом (α, β), где 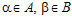, то для любого натурального числа n ≠ 1 через G_n будем обозначать подмножество группы G, состоящее из всех пар вида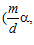 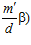 , где т, m′ – целые числа, взаимно простые с числом d, для каждого натурального делителя d числа п.

ЛЕММА 2. 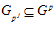, для любого натурального числа j.

Доказательство непосредственно следует из определения G ^р.

ПРЕДЛОЖЕНИЕ 1. Для любого простого числа р, выполняются условия:

1) подгруппа G ^р группы G является р-специальной подгруппой;

2) группа G ^р может быть получена как объединение бесконечной возрастающей цепи своих подгрупп 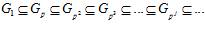, где ;

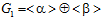3) система 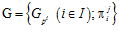, где 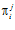– естественное вложение 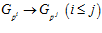, образует прямой спектр, причем .

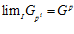Доказательство. Пусть р – простое число. Рассмотрим множество G ^р. По определению, 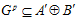, покажем, что множество G ^p образует подпрямую сумму групп  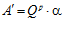и 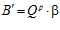, индуцированную группой Q ^р/Z, с базисом (α, β), причем группа G^р является подгруппой группы G.

Действительно, рассмотрим два произвольных элемента группы G ^p: 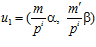 и 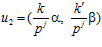, причем, 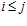. Поскольку рⁱ является делителем р ^j, то, по определению группы 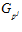, элементы и₁ и и₂, а также их сумма, принадлежат 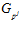, и, следовательно, множеству G ^р.

Таким образом, G ^р – группа.

Далее, пусть элемент 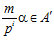, тогда числа т и рⁱ взаимно просты, и, следовательно, существует число m′ , взаимно  простое с числом рⁱ такое, что элемент 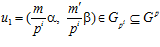, причем ни для какого числа m″ , несравнимого с числом     m′  по модулю рⁱ  в кольце Z, элемент .

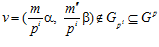Таким образом, проекция 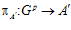является эпиморфизмом. Аналогично получаем, что проекция 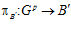также является эпиморфизмом. Следовательно, группа G^р есть подпрямая сумма групп A′  и B′, индуцированная группой Q ^р/Z.

Условие 2) непосредственно следует из определения группы G ^р, а также из определения групп 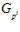 для каждого целого положительного числа i. Условие 3) предложения непосредственно следует из определения прямого спектра.

ПРЕДЛОЖЕНИЕ 2. Для любого элемента v группы G, не принадлежащего группе 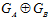, существуют и причем единственные, с точностью до нумерации, простые числа р₁, р₂, …, р_r такие, что v = v₀+ v₁ + v₂ + … + v_r, где ,
, , …, .

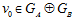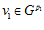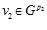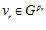   Доказательство. Пусть п – целое положительное число, отличное от единицы, такое, что 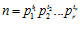, где числа р₁, р₂, …, р_r – различные простые, и пусть элемент 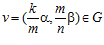, где числа k и т – целые, взаимно простые с числом п. Тогда, очевидно, пара  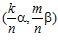может быть представлена в виде:

,

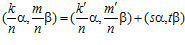где s и t – целые числа, а k’ и m’ - наименьшие целые положительные числа такие. что k′  сравнимо с k, а m′  сравнимо с т по модулю nZ в кольце Z. Пары 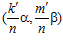 и (sα, tβ) принадлежат группе G, причем, как легко видеть, пара 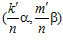может быть представлена в виде:

,

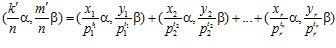где 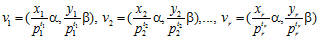. Что и требовалось доказать.

ЛЕММА. Для любого целого положительного числа k и любых целых взаимно простых чисел р₁, р₂, …, р_k выполняется условие: если сумма

,

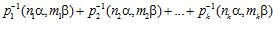где п₁, п₂, …, п_k, m₁, m₂, …, m_k – целые числа, причем, для каждого номера i = 1, 2, …, k выполняются условия: ,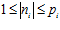
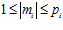, принадлежит группе G, то и каждый из элементов  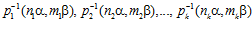принадлежит группе G.

Доказательство проведем методом математической индукции по числу k. Пусть k = 2, то есть сумма пар

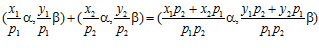
принадлежит группе G. Следовательно, если одна из пар 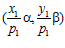 или 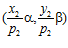 принадлежит группе G, то, очевидно, и другая пара также принадлежит группе G. Поэтому, предположим, что никакая из пар 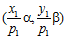и 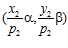 не принадлежит подпрямой сумме G групп А и В, индуцированной группой Q/Z. Но тогда, по определению подпрямой суммы групп, существуют целые числа 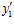,  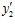такие, что

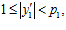
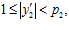
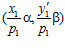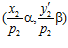и такие, что пары и  принадлежат группе G. Значит, и сумма

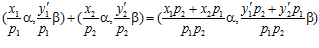
также принадлежит группе G. Тогда, числа у₁р₂ + у₂р₁ и 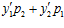 сравнимы по модулю р₁р₂ в кольце Z, следовательно, в кольце Z имеет место сравнение:

.

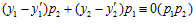Но, поскольку, для чисел 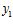, , 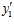,  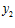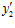выполняются условия:

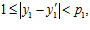
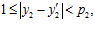
то сумма 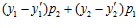равна либо нулю, либо р₁р₂. Тогда, в первом случае получаем, что 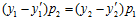. Следовательно, поскольку, по условию, числа р₁ и р₂ взаимно просты, то разность 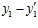делится на число р₁, а разность  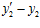делится на число р₂. Во втором случае, как нетрудно видеть, получаются точно такие же выводы.

Таким образом, в кольце Z имеют место сравнения: 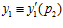, , 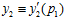и, значит, пары 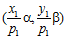и 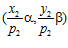 есть элементы группы G. 

Далее предположим, что для любого числа пар – слагаемых, меньшего числа k, лемма выполняется. Тогда, взяв сумму пар

,

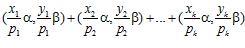и, разбив ее произвольным образом на сумму двух слагаемых, мы, используя предположение индукции и изложенные выше рассуждения, легко сможем показать, что каждая из пар 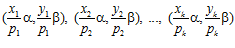принадлежит G. Следовательно, по принципу индукции, лемма выполняется для любого числа пар – слагаемых.

ТЕОРЕМА 3. 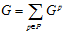, причем для любых различных простых чисел р и q справедливо равенство: 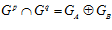, где группы G_A и G_B – ядра подпрямой суммы G групп А и В.

Доказательство. Легко видеть, что для любого простого числа р группа G^p является подгруппой группы G. Следовательно, .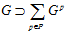

Обратно. По предложению 2 пара 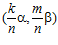, где числа k и т – целые, взаимно простые с числом п, может быть представлена в виде: 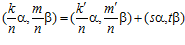, где s и t – целые числа, а k′  и m′  – наименьшие целые положительные числа такие, что    k′ сравнимо с k, а m′  сравнимо с т по модулю nZ в кольце целых чисел Z, а пара  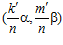может быть представлена в виде:

,

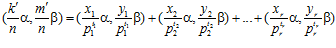где, по лемме, каждое слагаемое принадлежит группе G. Следовательно, 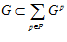. Таким образом, .

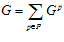Второе равенство в условии теоремы очевидно. Теорема доказана.

СЛЕДСТВИЕ. Пусть для каждого простого числа р, через Н ^р обозначим подпрямую сумму рациональных групп  A′  и B′ ,

изоморфных группе Q ^р и являющихся подгруппами групп А и В, соответственно, индуцированную группой Q ^р/Z, с одним и тем же базисом (α, β) . Тогда для каждого множества 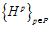, подпрямая сумма G групп А и B, индуцированная группой Q/Z, с базисом (α, β)  такая, что Н ^р= G ^p, существует и единственна.

Доказательство. Пусть дано некоторое множество 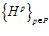подпрямых сумм рациональных групп A′  и B′ , изоморфных группам Q ^р, для каждого простого числа р, и являющихся подгруппами групп А и В, соответственно, индуцированных группами Q ^р/Z, с одним и тем же базисом (α, β). Тогда, применив рассуждения, аналогичные приведенным в теореме, мы получим, что .

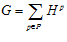ОПРЕДЕЛЕНИЕ. Последовательность целых положительных чисел

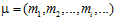
будем называть характеристической последовательностью группы G ^р для данного базиса (α, β) , если для каждого номера i, число т_i является наименьшим положительным, таким, что элемент 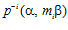принадлежит р-специальной подгруппе G ^р группы G, где р – простое число.

Поскольку, с точностью до знака, подпрямая сумма двух изоморфных рациональных групп имеет два базиса, то и характеристических последовательностей у такой подпрямой суммы будет две. Условие, описывающее характеристическую последовательность, и условие, связывающее характеристические последовательности одной и той же подпрямой суммы данных групп сформулированы в следующих предложениях.

ПРЕДЛОЖЕНИЕ 4. Последовательность целых положительных чисел 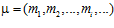является характеристической для некоторой р-специальной подгруппы G ^р группы G тогда и только тогда, когда выполняются условия:

1. 0 < т_i < рⁱ, для каждого номера i = 1, 2, …;
   
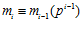2.  для каждого номера i = 2, 3, ….
   

Доказательство непосредственно следует из определения подпрямой суммы, характеристической последовательности.

СЛЕДСТВИЕ. Характеристическая последовательность группы G ^р сходится к некоторому целому р-адическому числу ρ  – единичному элементу кольца целых р-адических чисел.

Доказательство непосредственно следует из определения целого р-адического числа, а также из условия, что в данной последовательности отсутствуют нули.

Итак, на основании выше доказанных предложений мы можем сформулировать основную теорему.

ТЕОРЕМА 5. Для данного простого числа р существует взаимно-однозначное соответствие между множеством всех р-специальных групп с фиксированным базисом и мультипликативной группой обратимых элементов кольца целых р-адических чисел.

Существует взаимно-однозначное соответствие между множеством всех специальных групп с фиксированным базисом и мультипликативной группой обратимых элементов кольца универсальных чисел – 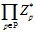, где 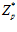 – кольцо целых р-адических чисел.

1. Trukhmanov V.B. On subdirect sums of abelian torsion-free groups of rank 1. // Journal of Mathematical Sciences. 2008. Т.154. №3. – С. 422-429.
2. Куликов Л.Я. О подпрямых суммах абелевых групп без кручения первого ранга // ХII Всес. алгебр. коллоквиум. – Свердловск. 1973. – С. 30.
3. Куликов Л.Я. Подпрямые разложения счетных абелевых групп без кручения // Х Всес. алгебр. коллоквиум. – Новосибирск. 1969. – С. 18-19.
4. Трухманов В.Б. Подпрямые суммы абелевых групп без кручения ранга 1. // Фундаментальная и прикладная математика. 2007. Т.13. №3. – С. 209-221.
5. Фукс Л. Бесконечные абелевы группы, т.1. – М. Мир, 1974.
6. Широков Л.В. О -бикомпактах. // Известия РАН. 1992. т. 56. № 6. – С. 1316-1327.
7. Широков Л.В. О продолжении непрерывных отображений и аппроксимативной связности // Проблемы современной науки, Центр научного знания «ЛОГОС». 2013. Выпуск 9. – С. 3-9.
8. Широков Л.В. Теория аналитических функций. Аспекты приложений / Л.В. Широков, Н.П. Ямпурин, В.Д. Садков. – Арзамас: АГПИ, 2004. – 188 с.

Все статьи автора «Трухманов Вячеслав Борисович»