Существуют два метода модификации полимеров путем введения пластифицирующих добавок – молекулярная пластификация и структурная пластификация. Первая подразумевает изменение механических свойств путем введения в них, в основном, низкомолекулярных веществ, совмещающихся с полимером на молекулярном уровне. Здесь, благодаря взаимодействию полимера с молекулами пластификатора, ослабляются силы взаимодействия макромолекул между собой. Из-за этого появляется возможность взаимной перегруппировки звеньев макромолекул под влиянием внешних механических полей и, соответственно, увеличивается податливость системы. Вторая связана с эффектом изменения механических свойств при введении относительно малых количеств низкомолекулярных веществ, практически не совместимых с полимером; пластификатор распределяется между элементами структуры в виде тонких слоев и оказывает эффект «смазки» (в качестве пластифицирующей добавки использовалось минеральное машинное масло (ММ)).
Химический состав минеральных и растительных масел очень сложен. Они содержат парафиновые, нафтеновые, ароматические, асфальто-смолистые вещества, а также смеси высоконепредельных, непредельных и предельных жирных кислот с рядом других углеводородов. Часть этих веществ по отношению к эпоксидной смоле являются реакционно-способными пластификаторами и осуществляют молекулярную пластификацию, другая же часть, практически несовместима с эпоксидной смолой и выступает в качестве структурного пластификатора. В случае использования модификаторов типа ММ имеет место комплексная пластификация. Некоторая часть молекул пластификатора вступает во взаимодействие с молекулами полимера, расслабляя силы взаимодействия макромолекул между собой. Одновременно другая часть молекул пластификатора ММ своими углеродными радикалами раздвигает цепи макромолекул полимера, создавая плоскости проскальзывания.
В [1,2] приводятся данные по определению зависимости вязкости В эпоксидного композита на основе эпоксидной смолы ЭД-16 от температуры t C и специальных добавок (ММ) в различных концентрациях x, % (табл.1).

Самой простой, но и достаточно грубой является ступенчатая аппроксимация. Ее можно применять или при мелкой сетке в пространстве аргумента x , или при специальном ступенчатом виде самой функции. Для приближения функции нескольких переменных можно воспользоваться ее представлением суммой функций одной переменной и методом наименьших квадратов. Для случая функции двух переменных  с прямоугольной областью изменения аргументов

соответствующее выражение имеет вид

.

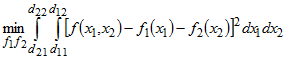Решение задачи получается в виде

где

,

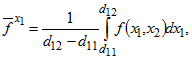
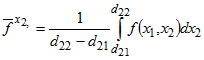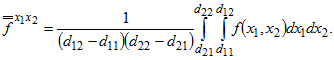
Задача приближения функции двух аргументов представлением в виде произведения двух одномерных аргументов сводится к только что рассмотренной. Действительно, если вместо исходной функции  рассмотреть функцию , выполнить приближение этой функции суммой , а затем образовать функцию

то

 

Существует относительно простой способ приближения многомерных таблично заданных функций обобщенными многочленами частного вида. В частности при двумерной аппроксимации аппроксимирующий многочлен определяется в виде

,

где  – выбранные из практических соображений функции,  – неизвестные коэффициенты. Для определения коэффициентов  можно воспользоваться методом наименьших квадратов; минимизация

,

где  – табличные значения . Здесь неизвестные  определяются из системы уравнений

где

.

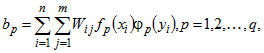
На основе предложенного подхода определялась оптимальной концентрации пластификатора – машинного масла; использовался метод сечений (результаты аппроксимации функций полиномами третьей степени на рис. 1 и 2; на рис. 3 – аппроксимация  функциями вида ; полиномиальная аппроксимация  при различных степенях полинома – на рис.4). Таким образом, с очевидностью следует возможность аппроксимации  в виде

Как видим, оптимальная концентрация пластификатора – машинного масла составляет 10 % (на 2–4 молекулы смолы приходится 1 молекула пластификатора).

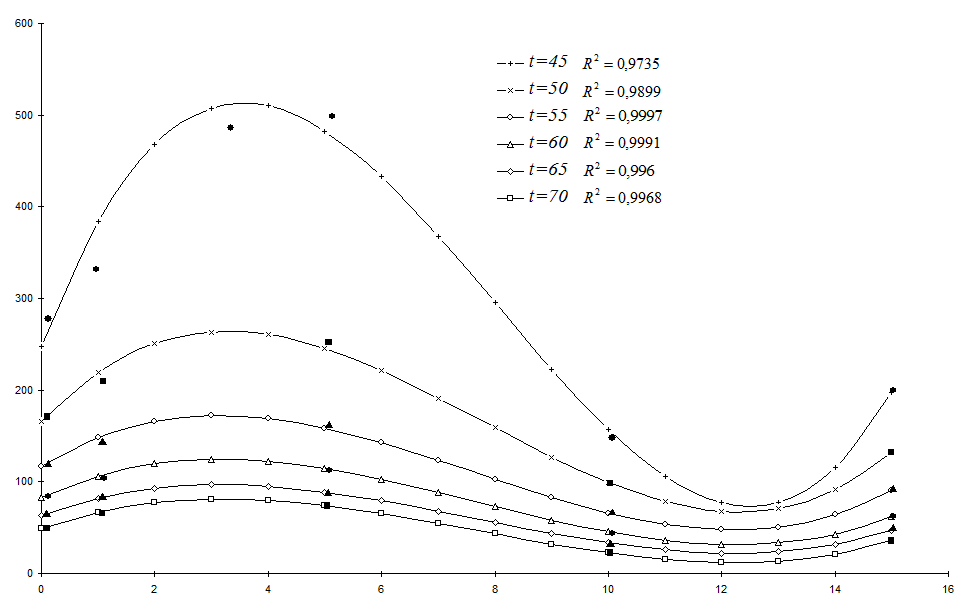Рис.1. Зависимость вязкости от температуры

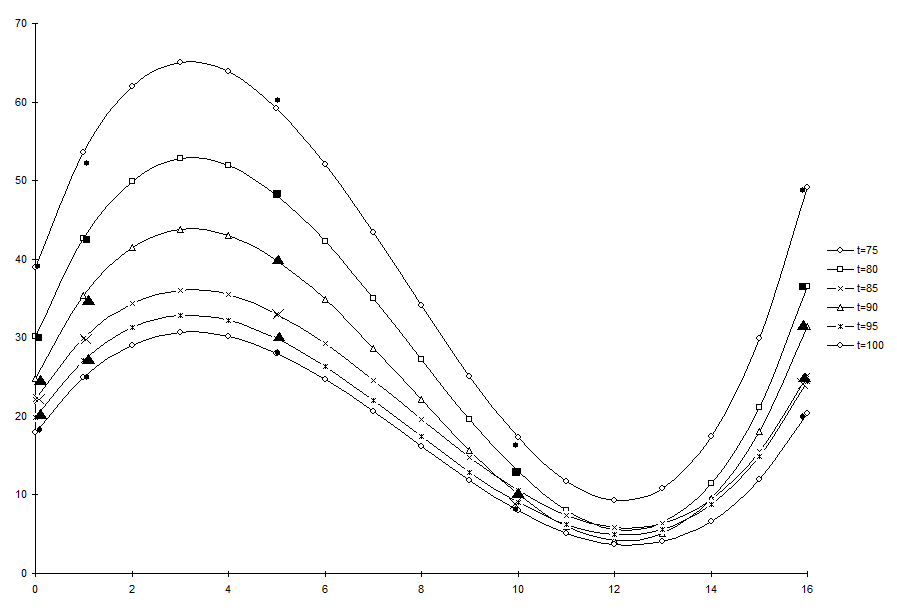
Рис.2

Рис. 3

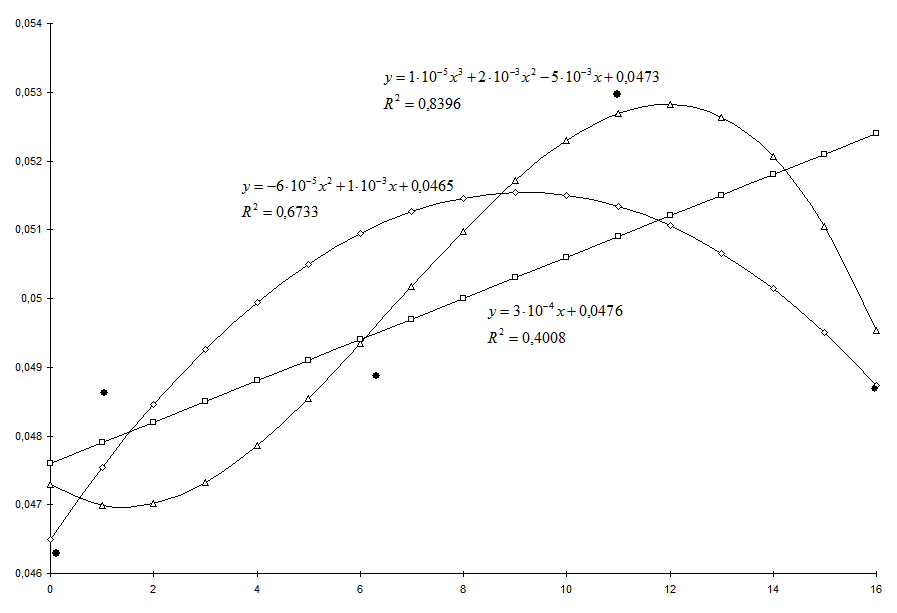
Рис. 4

Рассмотренный подход оказался эффективным и при решении других задач прикладного характера [3…7].

1. Бормотов А.Н., Прошин А.П., Данилов А.М. Разработка и управление качеством эпоксидных композитов для защиты от радиации (монография) / – Пенза: ПГУАС. – 2004. – 158 с.
2. Бормотов А.Н., Прошин И.А., Васильков А.В. Теоретические основы компьютерного моделирования структурообразования дисперсных систем / Вестник Тамбовского государственного технического университета. – 2011. -Т. 17. - № 2. -С. 542-551.
3. Данилов А.М., Гарькина И.А. Современная общая методология идентификации систем: моделирование свойств материалов / Региональная архитектура и строительство.  – 2010. – №1 (8). –  С.11-14.
4. Будылина Е.А., Гарькина И.А., Данилов А.М. Декомпозиция динамических систем в приложениях / Региональная архитектура и строительство. – 2013. – № 3. – С. 95-100.
5. Данилов А.М., Гарькина И.А. Интерполяция, аппроксимация, оптимизация: анализ и синтез сложных систем: монография. – Пенза: ПГУАС. –2014. – 168 с.
6. Гарькина И.А., Данилов А.М., Королев Е.В., Смирнов В.А. Преодоление неопределенностей целей в задачах многокритериальной оптимизации на примере разработки сверхтяжелых бетонов для защиты от радиации / Строительные материалы – Наука. – 2006. – № 8. – С.23-26.
7. Гарькина И.А., Данилов А.М., Петренко В.О. Проблема многокритериальности при управлении качеством сложных систем / Мир транспорта и технологических машин. –2013. –№ 2 (41). –С. 123-129.

Все статьи автора «fmatem»