Рассмотрим переходные процессы с короткой продолжительностью и отчетливо выраженными началом и концом. В инженерной практике часто анализ таких процессов допустим как детерминированных. Естественно, при этом требуется правильная интерпретация результатов. Теоретически такой процесс можно анализировать, как и любой нестационарный, путем осреднения по ансамблю. Аналогичные методы используются при определении нестационарных корреляционных функций, оценок плотности распределения, переменных во времени среднего значения и среднего значения квадрата. Практически изучение спектральной структуры переходных процессов во многих случаях можно и более простыми методами.
Действительно, рассмотрим реализацию  переходного процесса , принимающую значения, отличные от нуля, только в интервале . Пусть  поступает на вход системы с весовой функцией . Тогда 
при 0 > t > T₁,
 при ;
 - малая, но физически значимая, отличная от нуля величина. 
Спектром Фурье 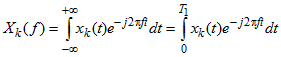 (преобразование Фурье функции) описываются спектральные свойства функции . В тригонометрической форме , - модуль, - аргумент .
Для энергетической спектральной плотности переходного процесса  справедливо:

;

а переходная взаимная спектральная плотность процессов ,  имеет вид:

.

Если

; 

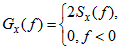
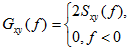
есть односторонние спектральные плотности, то при известной реализации  длительностью  имеет место

.

Откуда с учетом

,

оценку частотной характеристики можно определить в виде

.

Заметим, наиболее эффективное подавление случайных ошибок при оценке частотных характеристик достигается при осреднении по ансамблю оценок, вычисленных для независимых реализаций входных и выходных переходных процессов. Известно, оценка частотной характеристики не зависит от длины реализации T. Поэтому увеличение Т не приведет к повышению точности оценки. Скорее наоборот, при увеличении Т случайные ошибки могут возрасти, поскольку при этом увеличится вклад внешних помех при расчете функций  и .
Таким образом, очевидна последовательная процедура оценки частотной характеристики одномерной разомкнутой системы:

;
.

Для системы с одним выходом и со многими коррелированными входами частотные характеристики могут быть определены из решения системы линейных уравнений:

;

 - входные процессы,  - выходной процесс; целесообразно определять методом быстрого преобразования Фурье.
Далее. Детерминированная функция  определяет среднюю реакцию системы на некоторый средний входной сигнал (детерминированную функцию). Для уяснения физического смысла происходящих в системе процессов рассмотрим сглаживание реализаций  (рис. 1).

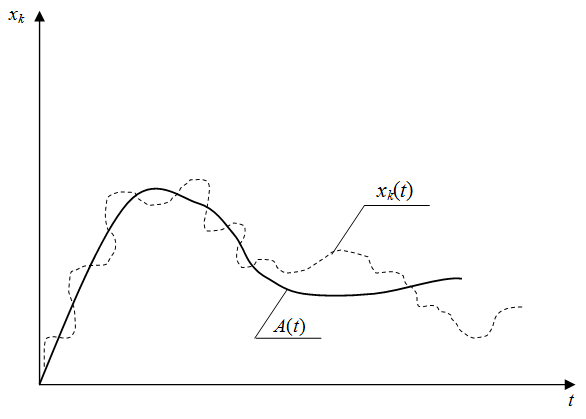
Рис. 1

Простейшим методом является осреднение ординат кривой на некотором интервале около фиксированного t (скользящая средняя). Получим следующую оценку математического ожидания случайного процесса  по одной реализации :

Разбив интервал Т₀ на m равных частей по формуле прямоугольников, получим:

.

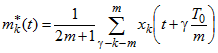Интервал Т₀ следует выбирать так, чтобы в интервале длиной 2Т₀ с центром в точке t математическое ожидание было приблизительно линейно (более строго требуется также малость среднего значения корреляционной функции ) в квадрате с центром в точке (t,t’) и стороной 2Т₀. При дополнительном усреднении по ансамблю N реализаций получим:

.

Одним из возможных способов определения по нескольким реализациям является одновременное сглаживание всех реализаций. Для применения этого способа следует построить все реализации случайной функции на одном графике. Тогда при правильно выбранном масштабе эти реализации образуют отчетливую полосу. Проведя на глаз среднюю линию этой полосы, получим кривую, которую можно принять за оценку математического ожидания. Способ глазомерного сглаживания обладает большей простотой. Однако недостатком этого способа является его субъективность. Предыдущий метод лишен этого недостатка. 
Изложенный прием сглаживания можно использовать для определения корреляционной функции, так как она представляет собой некоторое математическое ожидание. Для этого по экспериментальной кривой  случайного процесса  следует построить графики функции

для различных значений . Сгладив эти кривые, получим оценку значений корреляционной функции  (рис. 2).

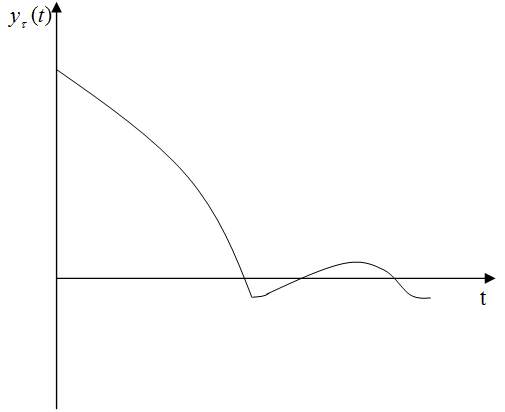
Рис. 2

Рассмотрим теперь разомкнутую линейную систему вида

Пусть

,

 и  получаются изложенным выше способом. Тогда в результате прямого преобразования Фурье получим комплексные частотные спектры детерминированных функций  и соответственно:

, ;

 характеризует в среднем частотную передаточную функцию системы для неустановившегося режима; .  могут быть получены методом БПФ. В частном случае, когда есть дельта-функция, будет представлять собой импульсную переходную функцию

.

Во многих случаях изложенные способы оказываются основными при анализе и синтезе человеко-машинных систем; входным сигналом здесь является управляющее воздействие (некоторая функция ошибки), выходом – регулируемая величина. Их апробация приводится в [1…10].

1. Будылина Е.А., Гарькина И.А., Данилов А.М. Декомпозиция динамических систем в приложениях / Региональная архитектура и строительство. – 2013. – № 3. – С. 95-100.
2. Гарькина И.А., Данилов А.М., Ермолаева Е.И., Зарецкий А.М. Сложные системы модульной структуры: композиты, автономные исследования сепаратных подсистем / Известия Казанского государственного архитектурно-строительного университета. – 2011. – № 1 (15). – С. 152-156.
3. Гарькина И.А., Данилов А.М., Домке Э.Р. Промышленные приложения системных методологий, теорий идентификации и управления / Вестник МАДИ. –  2009. – № 2(17). –  С.77-82.
4. Будылина Е. А., Гарькина И. А., Данилов А.М. Моделирование с позиций управления  в технических системах / Региональная архитектура и строительство. –2013. – № 2 (16). – С. 138-142.
5. Данилов А.М., Гарькина И.А. Интерполяция, аппроксимация, оптимизация: анализ и синтез сложных систем: монография. – Пенза: ПГУАС. –2014. – 168 с.
6. Будылина Е.А., Гарькина И.А., Данилов А.М., Пылайкин С.А. Аналитическое определение имитационных характеристик тренажных и обучающих комплексов // Фундаментальные исследования. – 2014. – № 6 (часть 4). – стр. 698-702.
7. Гарькина И.А., Данилов А.М., Пылайкин С.А. Тренажеры и имитаторы транспортных систем: выбор параметров вычислений, оценка качества / Мир транспорта и технологических машин. –№3(42). –2013. –С.115-121.
8. Данилов А.М., Гарькина И.А., Домке Э.Р. Математическое моделирование управляющих воздействий оператора в эргатической системе / Вестник МАДИ, №2, 2011. –С.18-23
9. Гарькина И.А., Данилов А.М., Королев Е.В., Смирнов В.А. Преодоление неопределенностей целей в задачах многокритериальной оптимизации на примере разработки сверхтяжелых бетонов для защиты от радиации / Строительные материалы – Наука. – 2006. – № 8. – С.23-26.
10. Гарькина И.А., Данилов А.М., Петренко В.О. Проблема многокритериальности при управлении качеством сложных систем / Мир транспорта и технологических машин. –2013. –№ 2 (41). –С. 123-129.

Все статьи автора «fmatem»