Постановка задачи
Рассмотрим гибридную стохастическую систему с последействием, описываемую уравнением
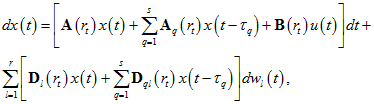
где ![]() – постоянные запаздывания;
– постоянные запаздывания; ![]() – независимые между собой и не зависящие от начального состояния системы (1) стандартные винеровские процессы;
– независимые между собой и не зависящие от начального состояния системы (1) стандартные винеровские процессы; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() – постоянные матрицы соответствующих размеров
– постоянные матрицы соответствующих размеров ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() – n-мерный вектор состояния;
– n-мерный вектор состояния; ![]() –мерный управляющий вектор;
–мерный управляющий вектор; ![]() - марковская цепь с дискретным множеством состояний
- марковская цепь с дискретным множеством состояний ![]() и матрицей вероятностей перехода
и матрицей вероятностей перехода ![]()
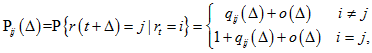
где ![]() ,
, ![]() для
для ![]() ,
, ![]() и
и ![]() называются интенсивностями перехода.
называются интенсивностями перехода.
Получим постоянное (не переключаемое) управление с обратной связью
![]()
которое гарантирует робастную устойчивость системы (1).
Основной результат
Подставим (2) в (1), получим:
.gif)
Сформулируем условия робастной стабилизации системы (1) на основе систем сравнения следующего вида:
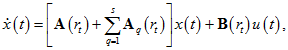
.gif)
Введем обозначения ![]()
Пусть матрицы Н > 0 и К удовлетворяют системе уравнений
![]()
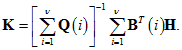
Тогда [1] закон управления (2) с матрицей управления (7) минимизирует функционал
.gif)
по отношению к системе
![]()
Справедлива следующая теорема.
Теорема 1. Пусть матрицы Н > 0 и К, для некоторых положительных симметричных матриц М(i), Q(i) и постоянной матрицы Q, удовлетворяют уравнениям (6), (7) и матрицы
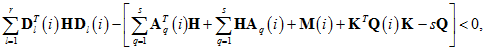

где
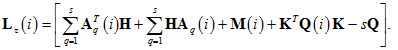
Тогда закон управления (2), (7) обеспечивает робастную устойчивость системы (1).
Доказательство. Выберем функционал Ляпунова-Красовского в форме:
.gif)
Тогда для производящего дифференциального оператора, примененного к функции V(x), с учетом (6), получим:
![]()
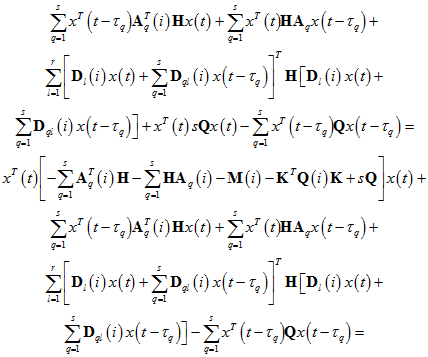
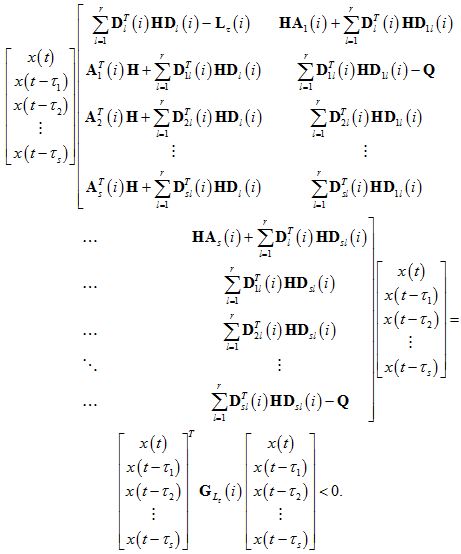
По теореме 11 раздела 2.3 [2] это неравенство гарантирует робастную устойчивость системы (3). Доказательство завершено.
Сформулируем аналогичную теорему на основе системы сравнения (5).
Теорема 2. Если для некоторых положительно определенных матриц ![]() и постоянной симметричной матрицы
и постоянной симметричной матрицы ![]() существуют матрицы Н > 0 и К, удовлетворяющие системе уравнений
существуют матрицы Н > 0 и К, удовлетворяющие системе уравнений
.gif)
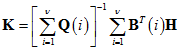
и системе неравенств
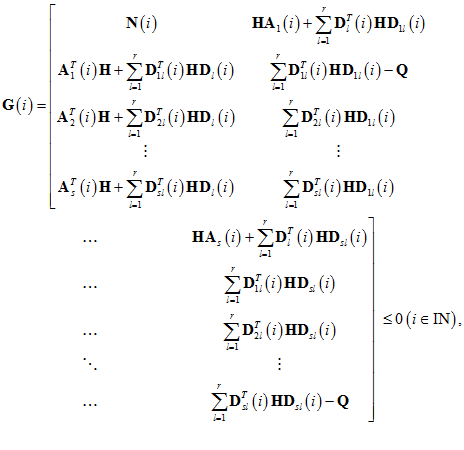
где
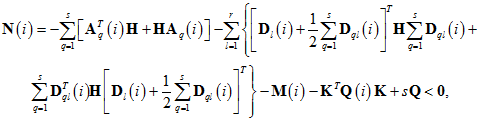
тогда закон управления (2) с матрицей К в виде (9) гарантирует робастную устойчивость системы (1).
Доказательство аналогично доказательству предыдущей теоремы.
Выводы.
В работе рассмотрена задача синтеза робастного управления с обратной связью по вектору состояния системами с запаздыванием.
Под робастным понимается управление с обратной связью, которое гарантирует асимптотическую устойчивость в среднем квадратическом (АУСК) системы при произвольных величинах запаздывания и при этом его структура остается постоянной для всех режимов, а параметры не зависят от вероятностных характеристик смены режимов.
Синтезированное управление является только стабилизирующим управлением, но когда в системе отсутствует запаздывание управление становится оптимальным. Можно сказать, что рассматривалась задача синтеза стабилизирующего управления системами с запаздыванием на основе оптимального управления систем сравнения без последействия.
Получены дополнительные условия, накладываемые на оптимальное управление системы без последействия, когда в системе появляется запаздывание.
Подобная проблема может возникнуть, например, при нарушении гипотезы стационарности обтекания плоскостей летательного аппарата. Гипотеза стационарности может нарушаться при возникновении скоса потока за крылом ЛА, что происходит при маневре с резким изменением угла атаки.
Аналогичные результаты, основанные на алгоритмах синтеза оптимального управления системами сравнения без последействия другого вида приведены в работе [3].
Библиографический список
- Pakshin P.V.: Robust stability and stabilization of the family of jumping stochastic systems // Nonlinear Analysis, Theory Methods & Apllications, 1997. V.30. P.2855-2866.
- Яблонский Д.В. Устойчивость и управление гибридными системами с запаздыванием. Germany: LAP LAMBERT Academic Publishing, 2012, 105 с.
- Яблонский Д.В. Синтез робастного управления гибридными стохастическими системами с запаздыванием // Актуальные проблемы гуманитарных и естественных наук. 2014. № 8.
