Определение всех используемых понятий, терминов и обозначений можно найти в работах 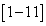 . Компакт – компактное хаусдорфово пространство, не обязательно метризуемое. Все пространства предполагаются вполне регулярными. В работе рассматриваются лишь такие спектры, проекции которых являются открыто-замкнутыми сюръективными отображениями.
. Компакт – компактное хаусдорфово пространство, не обязательно метризуемое. Все пространства предполагаются вполне регулярными. В работе рассматриваются лишь такие спектры, проекции которых являются открыто-замкнутыми сюръективными отображениями.
Определение 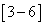 . Пусть
. Пусть 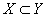 . Оператор продолжения е открытых множеств пространства
. Оператор продолжения е открытых множеств пространства 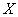 называется регулярным, если е удовлетворяет условиям:
называется регулярным, если е удовлетворяет условиям:
а) 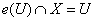 для любого открытого подмножества U пространства X;
для любого открытого подмножества U пространства X;
б) если U и V – открытые подмножества пространства X и 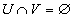 , то
, то 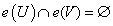 для любых
для любых 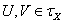 .
.
Определение. Отображение 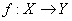 называется параллельным пространству Z, если существует регулярное вложение
называется параллельным пространству Z, если существует регулярное вложение 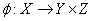 такое, что
такое, что 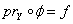 .
.
Следующее утверждение является основным результатом работы.
Теорема 1. Пусть 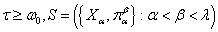 - непрерывный вполне упорядоченный спектр, причем сетевой вес
- непрерывный вполне упорядоченный спектр, причем сетевой вес 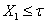 и все проекции
и все проекции 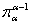 параллельны пространству сетевого веса
параллельны пространству сетевого веса 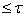 ,
, 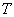 - всюду плотное подпространство
- всюду плотное подпространство 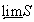
 и
и 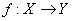 - непрерывное отображение
- непрерывное отображение 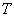 на пространство
на пространство 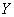 , причем характер
, причем характер 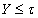 . Тогда сетевой вес
. Тогда сетевой вес 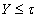 .
.
Доказательству теоремы 1 предпошлем несколько утверждений технического характера, которые, тем не менее, представляют и самостоятельный интерес.
Пусть 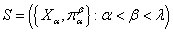 - непрерывный вполне упорядоченный спектр. Для любого
- непрерывный вполне упорядоченный спектр. Для любого 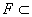
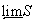 через
через 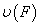 обозначим множество, содержащее 1 и все те непредельные
обозначим множество, содержащее 1 и все те непредельные 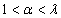 , что
, что
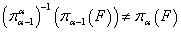 ,
,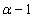 - предшествующий
- предшествующий 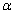 трансфинит. Если
трансфинит. Если 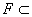
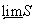 и
и 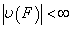 , то будем говорить, что множество
, то будем говорить, что множество 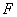 имеет конечный тип.
имеет конечный тип. Лемма 1. Естественное вложение предельного пространства непрерывного вполне упорядоченного спектра в произведение его элементов является регулярным.
Доказательство. Пусть
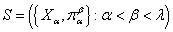 - непрерывный спектр с открытыми проекциями и
- непрерывный спектр с открытыми проекциями и 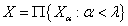 - произведение элементов спектра
- произведение элементов спектра 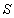 . Обозначим через
. Обозначим через 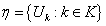 базу пространства
базу пространства 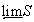 из открытых множеств конечного типа. Для каждого
из открытых множеств конечного типа. Для каждого 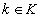 множество
множество
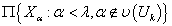
обозначим 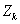 и положим
и положим
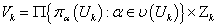 .
.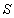 являются открытыми отображениями, то множество
являются открытыми отображениями, то множество 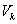 открыто в
открыто в 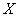 для любого
для любого 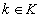 . Положим
. Положим 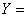
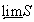 . Покажем, что для любого
. Покажем, что для любого 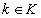 выполняется
выполняется 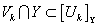 , т. е. что семейство
, т. е. что семейство 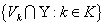 является базой пространства
является базой пространства 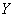 . Допустим, что существует
. Допустим, что существует 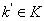 такое, что
такое, что 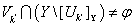 и пусть
и пусть 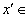
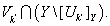 Выберем наименьшее
Выберем наименьшее 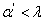 такое, что существует открытое множество
такое, что существует открытое множество  , содержащее
, содержащее 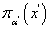 , причем
, причем 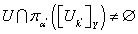 .
.Ясно, что
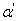 не является предельным и
не является предельным и 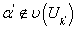 , но тогда
, но тогда 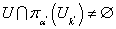 - противоречие. Покажем, что если
- противоречие. Покажем, что если 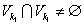 , то
, то 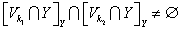 для любых
для любых 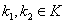 . Точку
. Точку 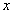 , принадлежащую множеству
, принадлежащую множеству
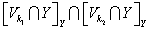 ,
,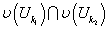 , обозначим через
, обозначим через 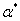 . Пусть
. Пусть 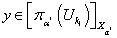
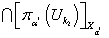 . Для каждого
. Для каждого 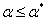 положим
положим 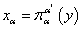 .
.Пусть
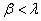 . Предположим, что для всех
. Предположим, что для всех 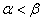 координаты
координаты 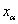 искомой точки найдены, причем
искомой точки найдены, причем
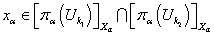 .
.1-й случай. 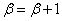 . Пусть
. Пусть 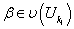 . Так как отображение
. Так как отображение 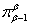 открыто-замкнуто, то
открыто-замкнуто, то
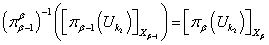
и
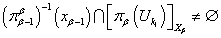 .
.Выберем некоторую точку
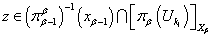
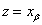 . Аналогично поступаем, если
. Аналогично поступаем, если 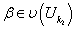 . Если
. Если 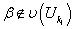 и
и 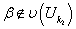 , то выберем произвольную точку
, то выберем произвольную точку 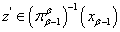 и положим
и положим 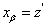 .
.2-й случай.
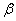 - предельное порядковое число. Выберем точку
- предельное порядковое число. Выберем точку 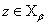 такую, что
такую, что 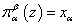 для любого
для любого 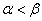 и положим
и положим 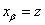 . Ясно, что
. Ясно, что
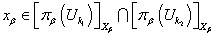 .
.Покажем, что точка
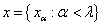 искомая. В самом деле, так как
искомая. В самом деле, так как 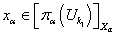 и
и 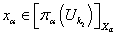 для любого
для любого 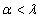 , то для любого
, то для любого 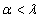 и любого отрытого множества
и любого отрытого множества 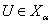 такого, что
такого, что 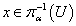 выполняется
выполняется 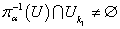 и
и 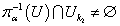 .
.Естественное вложение
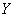 в
в 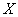 обозначим через
обозначим через 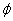 и для каждого открытого множества
и для каждого открытого множества 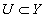 положим
положим 
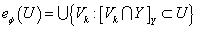 .
.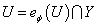 для любого открытого множества
для любого открытого множества 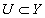 , причем, если
, причем, если 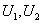 - открытые множества
- открытые множества 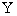 и
и 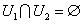 , то
, то 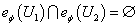 . Таким образом,
. Таким образом, 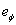 - искомый оператор продолжения открытых множеств. Лемма доказана.
- искомый оператор продолжения открытых множеств. Лемма доказана.Лемма 2. Пусть
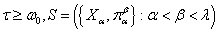 - непрерывный вполне упорядоченный спектр, причем
- непрерывный вполне упорядоченный спектр, причем  и для любого
и для любого 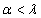 отображение
отображение 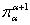 параллельно пространству
параллельно пространству 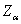 сетевого веса
сетевого веса 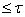 . Тогда существует регулярное вложение пространства
. Тогда существует регулярное вложение пространства 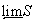 в тихоновское произведение
в тихоновское произведение 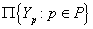 , причем сетевой вес
, причем сетевой вес 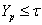 для любого
для любого 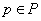 .
.Доказательство. Для каждого
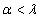 мы построим регулярное вложение
мы построим регулярное вложение 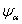 пространства
пространства 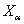 в тихоновское произведение
в тихоновское произведение 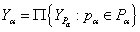 пространств сетевого веса
пространств сетевого веса 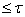 . Построение это проведем по трансфинитной индукции. Положим
. Построение это проведем по трансфинитной индукции. Положим 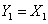 и
и 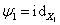 .
.Допустим, что для некоторого
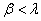 и всех
и всех 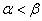 построение проведено.
построение проведено.1-й случай.
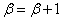 . Пусть
. Пусть 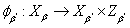 - регулярное вложение
- регулярное вложение 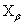 в
в 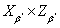 . Ясно, что вложение
. Ясно, что вложение 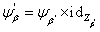 пространства
пространства 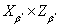 в пространство
в пространство 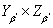 регулярно. Также очевидно, что вложение
регулярно. Также очевидно, что вложение 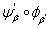 пространства
пространства 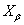 в пространство
в пространство  регулярно. Положим
регулярно. Положим 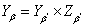 и
и 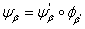 .
.2-й случай.
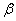 - предельный ординал. Обозначим через
- предельный ординал. Обозначим через 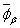 естественное вложение предельного пространства спектра
естественное вложение предельного пространства спектра 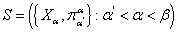 в произведение
в произведение  и положим
и положим 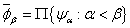 . Так как вложения
. Так как вложения 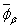 и
и 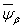 регулярны, то регулярно вложение
регулярны, то регулярно вложение 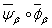 . Положим
. Положим 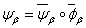 и
и 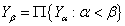 . Индукция завершена.
. Индукция завершена.Пусть
 - естественное вложение
- естественное вложение 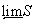 в
в 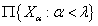 . Положим
. Положим 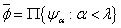 . Поскольку вложения
. Поскольку вложения 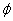 и
и 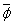 регулярны (для
регулярны (для 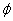 это следует из леммы 1), то регулярно вложение
это следует из леммы 1), то регулярно вложение 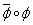 пространства
пространства 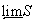 в тихоновское произведение
в тихоновское произведение 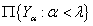 . Лемма доказана.
. Лемма доказана.Доказательство теоремы 1. По лемме 2 существует регулярное вложение
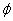 пространства
пространства 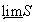 в тихоновское произведение
в тихоновское произведение 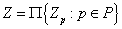 , причем
, причем 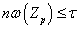 для любого
для любого 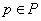 . Так как вложение
. Так как вложение 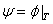 пространства
пространства 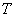 в
в 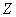 регулярно, то отображение
регулярно, то отображение 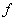 пространства
пространства 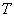 на пространство
на пространство  регулярно относительно
регулярно относительно 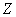 . Следовательно,
. Следовательно, 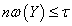 [1]. Теорема доказана.
[1]. Теорема доказана. Естественным продолжением обсуждаемых вопросов является следующее утверждение.
Теорема 2. Пусть
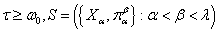 - непрерывный вполне упорядоченный спектр из компактов, причем
- непрерывный вполне упорядоченный спектр из компактов, причем 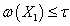 и все проекции
и все проекции 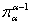 параллельны пространству веса
параллельны пространству веса 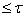 ,
, 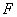 - замкнутое подмножество
- замкнутое подмножество 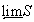 , причем
, причем 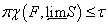 . Тогда существует замкнутое подмножество
. Тогда существует замкнутое подмножество 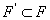 такое, что
такое, что 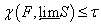 .
.Доказательство. Пусть
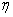 - определяющая система окрестностей множества
- определяющая система окрестностей множества 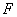 в пространстве
в пространстве 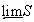 и
и 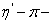 база множества
база множества 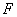 в
в 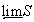 , причем
, причем 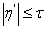 . Для каждого
. Для каждого  через
через 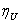 обозначим подсемейство семейства
обозначим подсемейство семейства 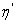 , состоящее из всех элементов
, состоящее из всех элементов 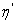 , содержащихся в
, содержащихся в 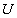 , и положим
, и положим 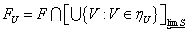 . Ясно, что для любого
. Ясно, что для любого 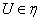 множество
множество 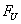 не пусто. Так как семейство
не пусто. Так как семейство 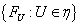 центрировано, то
центрировано, то 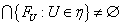 . Выберем точку
. Выберем точку 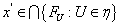 . По лемме 2 существует регулярное вложение
. По лемме 2 существует регулярное вложение 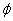 пространства
пространства  в тихоновское произведение
в тихоновское произведение 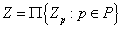 , причем
, причем  для каждого
для каждого 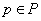 . Для каждого
. Для каждого  через
через 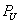 обозначим подмножество
обозначим подмножество 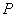 мощности
мощности 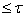 такое, что замыкание
такое, что замыкание 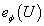 в
в 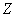 не зависит от
не зависит от 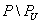 и положим
и положим 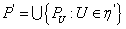 . Ясно, что
. Ясно, что 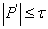 . Положим
. Положим 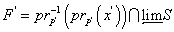 и покажем, что
и покажем, что 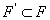 . Допустим, что существует точка
. Допустим, что существует точка 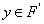 , не принадлежащая множеству
, не принадлежащая множеству 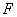 . Выберем
. Выберем  такое, что
такое, что 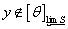 и положим
и положим 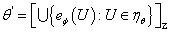 . Так как вложение
. Так как вложение 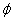 регулярно (лемма 1), то
регулярно (лемма 1), то 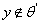 , и получаем противоречие с тем, что
, и получаем противоречие с тем, что 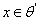 . Таким образом ,
. Таким образом , 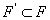 , а так как
, а так как 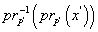 - слой в
- слой в 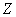 с основанием мощности
с основанием мощности 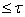 , то получаем , что
, то получаем , что 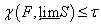 . Теорема доказана.
. Теорема доказана.Следствие. Пусть
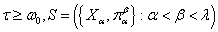 - непрерывный вполне упорядоченный спектр из компактов, причем
- непрерывный вполне упорядоченный спектр из компактов, причем 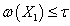 и все проекции
и все проекции 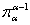 параллельны пространству веса
параллельны пространству веса 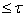 ,
, 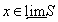 и
и 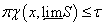 . Тогда
. Тогда  .
.Библиографический список
- Архангельский А.В. Об отображениях всюду плотных подпространств топологических произведений. // Докл. АН СССР. 1971. т. 197. № 4. С. 750 – 753.
- Дранишников А.Н. Абсолютные экстензоры в размерности n и n-мягкие отображения, повышающие размерность. // УМН. 1984. т. 39. вып. 5. С. 55 – 95.
- Широков Л.В. Внешняя характеристика пространств Дугунджи и -метризуемых бикомпактов. // Докл. АН СССР. 1982. т. 263. № 5. С. 1073-1077.
- Широков Л.В. О AE(n)-бикомпактах. // Известия РАН. 1992. т. 56. № 6. С. 1316 – 1327.
- Щепин Е.В. Топология предельных пространств несчетных обратных спектров. // УМН. 1976. т. 31. вып. 5. С. 191-226.
- Shirokov L.V. On some forms of embeddings of topological spaces. // Russian Mathematical Surveys 42, (2), 297-298.
- Широков Л.В. О продолжении непрерывных отображений и аппроксимативной связности // Проблемы современной науки, Центр научного знания «ЛОГОС». 2013. выпуск 9. С. 3–9.
- Широков Л.В. О -бикомпактах и -мягких отображениях. // Сиб. матем. журн. 1992. т. 33. № 2. С. 151-156.
- Широков Л. В. Теория аналитических функций. Аспекты приложений/Л. В. Широков, Н. П. Ямпурин, В. Д. Садков. -Арзамас: АГПИ, 2004. -188 с.
- Trukhmanov V.B. On subdirect sums of abelian torsion-free groups of rank 1. // Journal of Mathematical Sciences. 2008. Vol. 154. № 3. С. 422-429.
- Трухманов В.Б. Подпрямые суммы абелевых групп без кручения ранга 1. // Фундаментальная и прикладная математика. 2007. Т. 13. № 3. С. 209-221.
