Пусть Х- множество объектов, u={u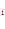 (x),…,u
(x),…,u (x)}-критерии первого уровня, к={к
(x)}-критерии первого уровня, к={к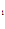 (х),…,к
(х),…,к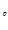 (х)
(х) } – критерии второго уровня, х
} – критерии второго уровня, х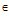 Х. При отсутствии критериев второго уровня задача поиска объекта решается на множестве Парето [1] x
Х. При отсутствии критериев второго уровня задача поиска объекта решается на множестве Парето [1] x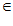 Argmin F(x), x
Argmin F(x), x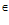 P
P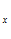 ,
,
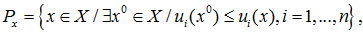
где F(x)-обобщенный критерий, представляющий свертку u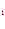 (x),…,u
(x),…,u (x).
(x).
В нашем случае задача решается следующим способом:
Шаг 1. Введем множество векторов предпочтения критериев первого уровня 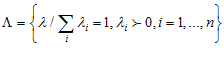 – представляющий собой n-1-мерный правильный симплекс. Для каждого
– представляющий собой n-1-мерный правильный симплекс. Для каждого 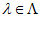 определим множества
определим множества
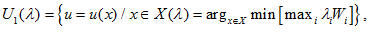
где 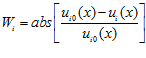 – нормированные критерии,
– нормированные критерии,
u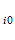 (x)= max u
(x)= max u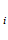 (x) или min u
(x) или min u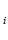 (x) если предпочтительно увеличение или уменьшение значения u
(x) если предпочтительно увеличение или уменьшение значения u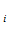 (x).
(x).
Если для фиксированного 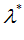
 получено несколько вариантов объекта
получено несколько вариантов объекта
Х (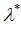 )
) 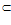 Х, то формируется множество
Х, то формируется множество
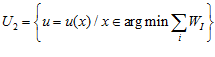 , для всех х
, для всех х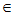 Х(
Х(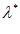 ).
).
Обозначим Р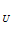 =
= 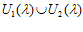 – множество не улучшаемых, с точки зрения по
– множество не улучшаемых, с точки зрения по 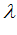 , векторов из U
, векторов из U 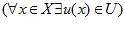 или вариантов объекта
или вариантов объекта 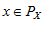 для которых
для которых 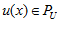 . Параметр
. Параметр 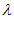 выполняет роль промежуточных переменных и определяет вариант объекта. Тогда поиск оптимального или точнее – рационального варианта объекта можно переформулировать как задачу поиска неизвестных
выполняет роль промежуточных переменных и определяет вариант объекта. Тогда поиск оптимального или точнее – рационального варианта объекта можно переформулировать как задачу поиска неизвестных  .
.
Шаг 2. Выбирая на симплексе точку 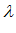 определяем для нее вариант объекта и с помощью моделирования определяем
определяем для нее вариант объекта и с помощью моделирования определяем
к (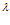 ) = {к
) = {к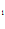 (
(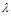 ),…,к
),…,к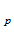 (
(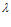 )
) }.
}.
Шаг 3. Обобщенный критерий представим в виде F(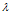 )=
)= 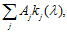 j=1,…,p, где
j=1,…,p, где 
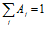 – коэффициенты предпочтения критериев второго уровня (назначают эксперты).
– коэффициенты предпочтения критериев второго уровня (назначают эксперты).
Шаг 4. Далее определяем 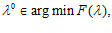 для
для 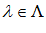 и соответствующий х
и соответствующий х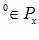 , для которого u(x
, для которого u(x )
)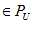 .
.
Данная постановка задачи формирует контур автоматизированного принятия решения, где эксперт на рекомендацию принять вариант объекта, имея информацию о u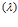 , k
, k 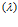 , F
, F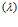 , за счет коррекции
, за счет коррекции 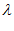 может получать и сравнивать варианты объекта, принадлежащие
может получать и сравнивать варианты объекта, принадлежащие 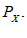 Для нахождения рационального варианта объекта на симплексе строят
Для нахождения рационального варианта объекта на симплексе строят 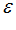 – сеть узлы которой есть компоненты вектора
– сеть узлы которой есть компоненты вектора 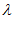 . Для
. Для 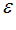 – сети формируют
– сети формируют 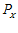 или
или 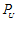 , что иногда представляет очень большую по объему вычислений задачу. Для преодоления этих трудностей воспользуемся симплексными планами Дрепера-Лоуренса [2,c.112]. В симплексной системе ими построен план, минимизирующий смещение (систематическую ошибку), связанное с тем, что истинная поверхность отклика описывается полиномом степени
, что иногда представляет очень большую по объему вычислений задачу. Для преодоления этих трудностей воспользуемся симплексными планами Дрепера-Лоуренса [2,c.112]. В симплексной системе ими построен план, минимизирующий смещение (систематическую ошибку), связанное с тем, что истинная поверхность отклика описывается полиномом степени 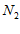 , а модель строится степени
, а модель строится степени 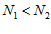 . Согласно плану на симплексе (для трех критериев) выбирается, по определенным правилам, семь точек. Для каждой точки вычисляют u (
. Согласно плану на симплексе (для трех критериев) выбирается, по определенным правилам, семь точек. Для каждой точки вычисляют u (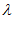 ), k (
), k (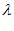 ), F(
), F(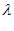 ). Далее определяем
). Далее определяем 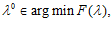 и соответствующий х
и соответствующий х . Вся информация передается экспертам, который может принять данный вариант или остановиться на любом другом из семи предложенных. Таким образом, определяется начальная, опорная, точка для дальнейшего поиска рационального варианта объекта.
. Вся информация передается экспертам, который может принять данный вариант или остановиться на любом другом из семи предложенных. Таким образом, определяется начальная, опорная, точка для дальнейшего поиска рационального варианта объекта.
Рассмотрим краткое описание нескольких процедур поиска рационального варианта объекта с учетом реакции эксперта.
Процедура 1 (метод “расширяющихся окрестностей”).
Рассматривается окрестность точки
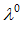
с радиусом
R=min{R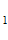 , R
, R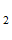 , R
, R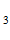 } / h
} / h , где R
, где R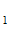 ,R
,R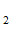 , R
, R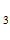 - расстояние от точки
- расстояние от точки 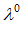
до сторон симплекса и целое h>1. Если координаты наилучшей точки в исходной системе координат 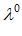 = {
= {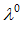
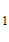 ,
, 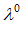
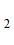 ,
, 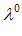
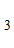 }, то в симплексной – надо умножить все компоненты на
}, то в симплексной – надо умножить все компоненты на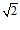 . Для заданного угла
. Для заданного угла  исследованию подлежат точки на окружности R с угловым шагом n
исследованию подлежат точки на окружности R с угловым шагом n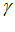 . Координаты точки
. Координаты точки 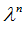 в симплексной системе вычисляются по формулам
в симплексной системе вычисляются по формулам
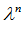
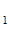 =
=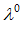
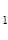 + R( cos n
+ R( cos n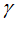 – sin n
– sin n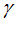 ),
),
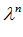
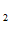 =
=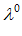
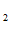
 - R
- R 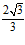 cos n
cos n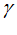 ,
,
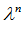
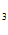 =
=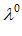
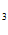 + R( sin n
+ R( sin n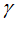 +
+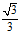 cos n
cos n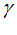 ).
).
При оценке решений х (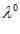 ) и х (
) и х (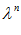 ) реакция эксперта может быть, например, вектор с компонентами +1, 0 , -1. Плюс 1 –если х (
) реакция эксперта может быть, например, вектор с компонентами +1, 0 , -1. Плюс 1 –если х (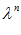 ) предпочтительнее х (
) предпочтительнее х (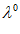 ) – тогда точка
) – тогда точка 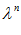 является исходной и процесс построения окрестностей R повторяется , 0 – в противном случае – процесс повторяется после выбора h
является исходной и процесс построения окрестностей R повторяется , 0 – в противном случае – процесс повторяется после выбора h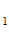 < h, минус 1 –если решения неразличимые. В последнем случае решение выбирается случайно.
< h, минус 1 –если решения неразличимые. В последнем случае решение выбирается случайно.
Процедура 2 (градиентный поиск).
Предположим, что в сколь угодно малой, локальной области симплекса функции К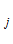 (
(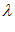 ) можно представить в виде полиномов первой степени
) можно представить в виде полиномов первой степени
К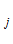 (
(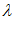 ) =
) =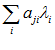 , (i=1,2,…,n
, (i=1,2,…,n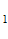 ; j=1,2,…n
; j=1,2,…n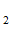 ). Доказано, что если градиенты функций К
). Доказано, что если градиенты функций К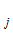 (
(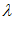 ) = С
) = С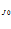 +
+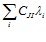 лежат в области симплекса, то градиент линейной свертки F(
лежат в области симплекса, то градиент линейной свертки F(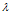 )=
)= 
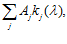 лежит в области симплекса, и направляющий вектор градиента имеет координаты
лежит в области симплекса, и направляющий вектор градиента имеет координаты
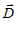 = {(А
= {(А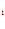 С
С +А
+А С
С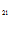 +…+А
+…+А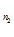 С
С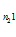 ), …,(А
), …,(А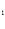 С
С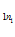 +А
+А С
С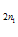 +…+А
+…+А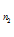 С
С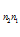 )}
)}
где С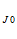 =
=
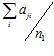 =
=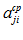 ,
, 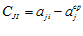 .
.
Около точки 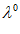 строится локальный симплекс АВС. Координаты точек
строится локальный симплекс АВС. Координаты точек 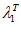 ,
, 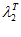 ,
, 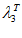 где Т
где Т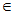 {А, В, С}, вычисляются для последовательных углов n
{А, В, С}, вычисляются для последовательных углов n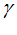 =0 , 2
=0 , 2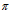 /3, 4
/3, 4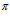 /3. С помощью моделирования в каждой точке вычисляем критерии второго уровня.
/3. С помощью моделирования в каждой точке вычисляем критерии второго уровня.
Запишем систему уравнений К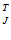 =
= 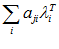 и решаем относительно
и решаем относительно 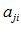 . Далее вычисляем С
. Далее вычисляем С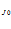 , С
, С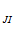 ,
, 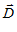 . Исходной точкой для движения по градиенту является центр локального симплекса. Движение осуществляется благодаря изменению компонент
. Исходной точкой для движения по градиенту является центр локального симплекса. Движение осуществляется благодаря изменению компонент 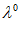 пропорционально координатам направляющего вектора
пропорционально координатам направляющего вектора 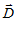 . Если найден вариант х (
. Если найден вариант х (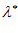 ) в точке
) в точке 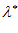 вокруг нее строится новый локальный симплекс А
вокруг нее строится новый локальный симплекс А В
В С
С и определяется новое направление движения.
и определяется новое направление движения.
Библиографический список
- Меркурьев В.В., Молдавский М.А. Семейство сверток векторного критерия для нахождения точек множества Парето. – Автоматика и телемеханика, 1979,№1,c.110-121.
- Зедгинидзе И.Г. Планирование эксперимента для исследования многокомпонентных систем. М.: Наука,1976.-377с.
