Используя модель автомобильной инфраструктуры региона, а также базу данных о состоянии дорог, возможно использование программы, предлагающей водителям оптимальный, с точки зрения времени, маршрут движения. Данная программа использует алгоритм Дейкстры и реализована в виде макроса в MS Excel.
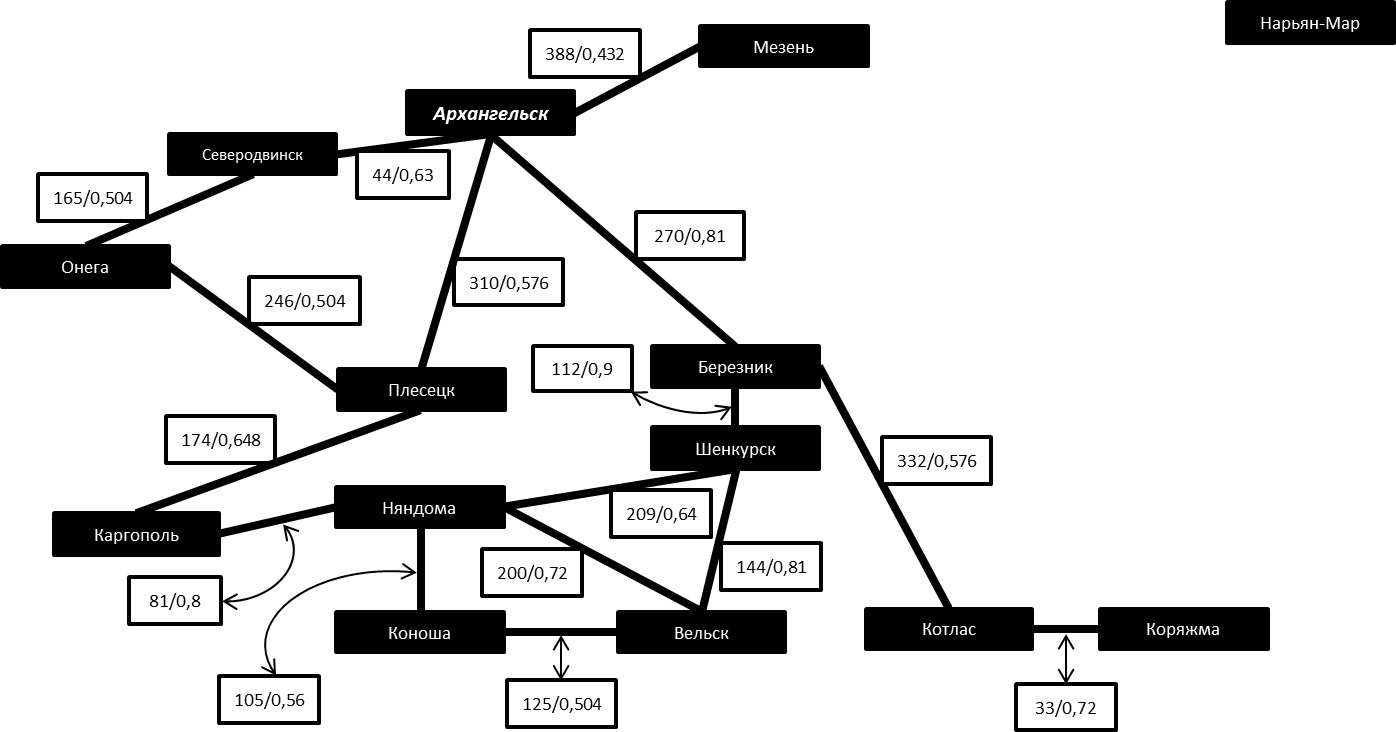
Рассмотрим моделирование транспортной сети на примере Архангельской области. Модель транспортной инфраструктуры Архангельского региона, представим в виде взвешенного графа, где вершины – населенные пункты, а ребра – дороги, имеющие в качестве «веса» 2 параметра: протяженность веток и понижающий коэффициент, определяющий среднюю скорость передвижения.
Рисунок 1- Граф автомобильных дорог
Для выполнения алгоритма необходимо представить граф в матричном виде. Используем в качестве способа матричного представления графа матрицу смежности.
Матрица смежности взвешенного графа – это квадратная матрица, значения элементов которой характеризуются смежностью вершин графа. В модели элемент матрицы смежности равен соответствующему весу ребра. Прочерк указывает на отсутствие ребра между вершинами . Весом ребра матрицы смежности является частное от деления расстояния на среднюю скорость движения на выбранном транспорте (таблица 1).
Таблица 1 – матрица смежности графа сети для грузовиков
|
Матрица смежности |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Мезень |
1 |
- |
- |
12,83 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
Северодвинск |
2 |
- |
- |
1,00 |
4,68 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
Архангельск |
3 |
12,83 |
1,00 |
- |
- |
4,76 |
7,69 |
- |
- |
- |
- |
- |
- |
- |
- |
|
Онега |
4 |
- |
4,68 |
- |
- |
- |
6,97 |
- |
- |
- |
- |
- |
- |
- |
- |
|
Березник |
5 |
- |
- |
4,76 |
- |
- |
6,88 |
1,78 |
- |
- |
0,16 |
- |
- |
- |
- |
|
Плесецк |
6 |
- |
- |
7,69 |
6,97 |
6,88 |
- |
- |
- |
0,07 |
- |
- |
- |
- |
- |
|
Шенкурск |
7 |
- |
- |
- |
- |
1,78 |
- |
- |
4,67 |
- |
- |
2,54 |
- |
- |
- |
|
Няндома |
8 |
- |
- |
- |
- |
- |
- |
4,67 |
- |
1,45 |
- |
3,97 |
2,68 |
- |
- |
|
Каргополь |
9 |
- |
- |
- |
- |
- |
3,84 |
- |
1,45 |
- |
- |
- |
- |
- |
- |
|
Котлас |
10 |
- |
- |
- |
- |
8,23 |
- |
- |
- |
- |
- |
- |
- |
0,65 |
- |
|
Вельск |
11 |
- |
- |
- |
- |
- |
- |
2,54 |
3,97 |
- |
- |
- |
3,54 |
- |
- |
|
Коноша |
12 |
- |
- |
- |
- |
- |
- |
- |
2,68 |
- |
- |
3,54 |
- |
- |
- |
|
Коряжма |
13 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,65 |
- |
- |
- |
- |
|
Нарьян-Мар |
14 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
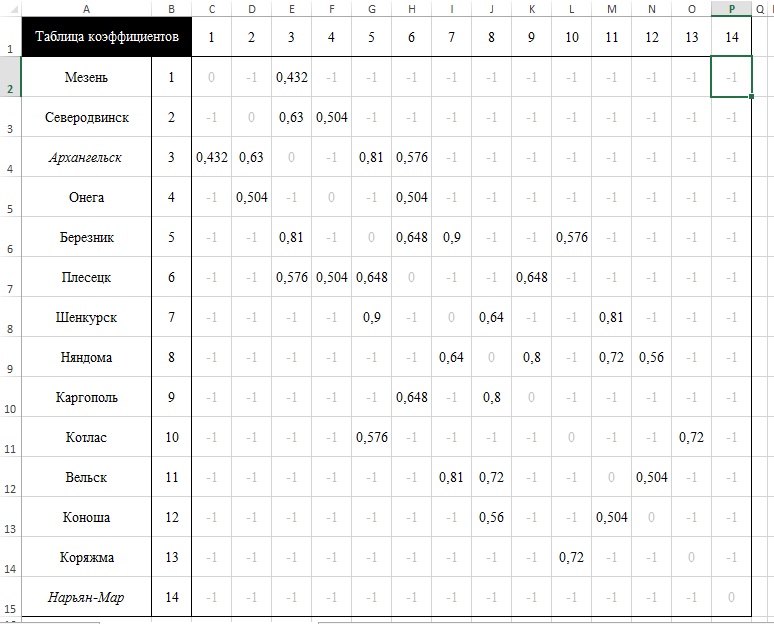
Значения матрицы смежности, с которой работает макрос, зависят от выбранного транспорта и коэффициента для соответствующего ребра (рисунок 2).
Рисунок 2 - Таблица коэффициентов
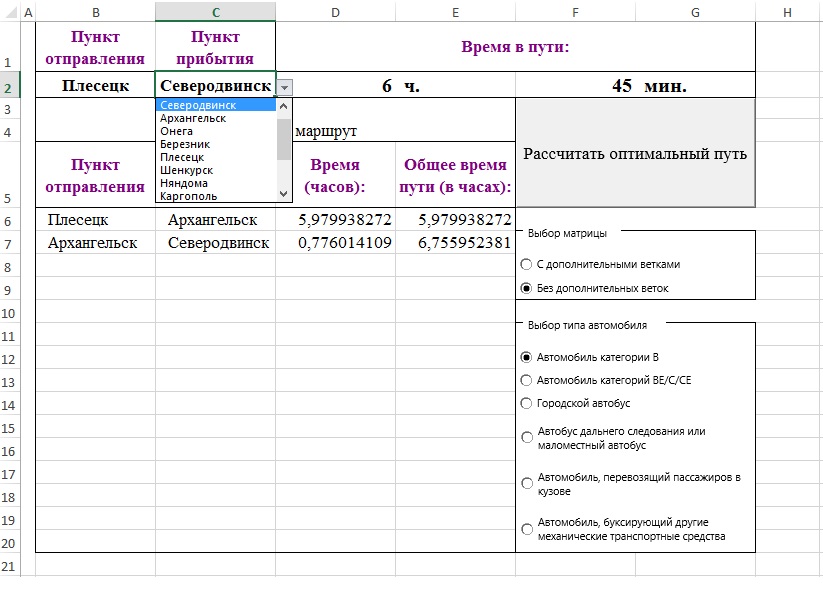
На рабочем листе имеются два раскрывающихся списка, с помощью которых выбираются пункты отправления и прибытия (рисунок 3).
Рисунок 3. Использование списка для выбора пунктов отправления и прибытия
Матрицы смежности, с которыми работает макрос, в зависимости от положения переключателя выбирают соответствующие диапазоны: Graph1 и Vertex1 при выборе модели с дополнительными ребрами и Graph2 и Vertex2 в ином случае. Graph1 и Graph2 – обозначение диапазона соответствующих значений матрицы смежности, а Vertex1 и Vertex2 – обозначение множества соответствующих имен вершин (рисунок 4).
Рисунок 4. Диспетчер имен в MS Excel
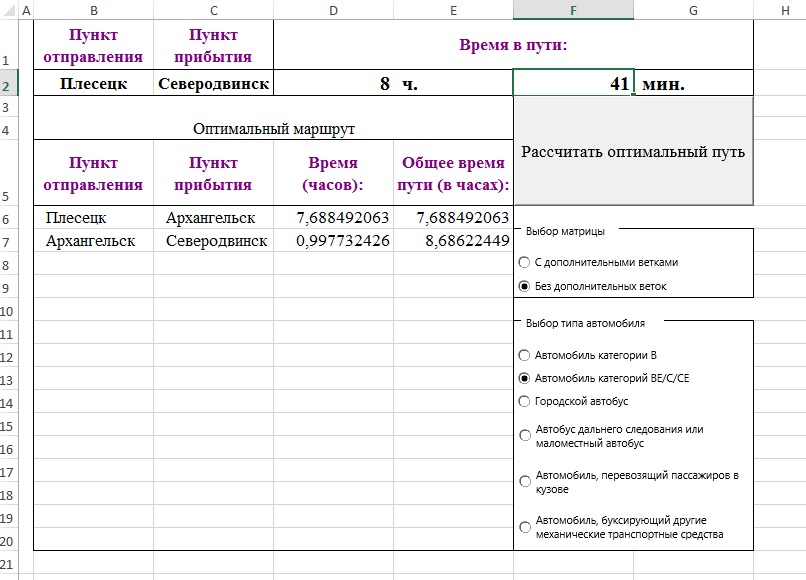
При нажатии на кнопку запускается макрос и выдается оптимальный маршрут и примерное время в пути (выводится в часах и минутах).
Рисунок 5. Пример расчета времени в MS Excel для выбранного маршрута
Библиографический список
- Домнин, Л.Н. Элементы теории графов: учеб. Пособие. Изд-во Пенз. Гос. Ун-та, 2007. – 144 с.
- Семенов В.В. Математическое моделирование динамики транспортных потоков мегаполиса. – М.: Институт прикладной математики им. М.В. Келдыша, 2004. – 44 с.
- Швецов В.И. Математическое моделирование транспортных потоков: Автоматика и телемеханика 2003.
- Алексеев В.Е., Таланов В.А. Графы. Модели вычислений. Структуры данных: Учебник. – Нижний Новгород: Изд-во ННГУ, 2005. 307 с.
- Демидова Л.А., Пылькин А.Н. – Программирование в среде Visual Basic for Applications: Практикум. – М.: Горячая линия – Телеком, 2004. – 175 с.
- Гасников А.В., Кленов С.Л., Нурминский Е.А., Холодов Я.А., Шамрай Введение в математическое моделирование транспортных потоков: Учебное пособие / Под редакцией Гасникова А.В. – М.: МЦНМО, 2012.
- Морозов И. И., Гасников А. В., Тарасов В. Н., Холодовa Я. А., Холодов А.С. Численное исследование транспортных потоков на основе гидродинамических моделей.
- Урыков В.А., Зеленина Л.И. Математические модели транспортных потоков // Современная техника и технологии. 2015. № 6 [Электронный ресурс]. URL: http://technology.snauka.ru/2015/06/6051 (дата обращения: 17.06.2015).