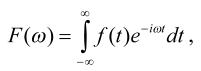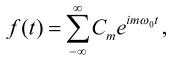Анализ зависимости напряжения или тока от времени широко используется для получения информации о качестве различных устройств. Однако просто зависимость определенных величин от времени в некоторых случаях не обладает достаточной чувствительностью к изменениям сигнала и не позволяет провести всесторонний анализ работы устройства. Более чувствительной является форма спектра сигнала, причем проводить спектральный анализ необходимо, например, при решении проблемы электромагнитной совместимости, когда требуется обеспечить работу многих радиоэлектронных средств в ограниченном диапазоне частот.
Если в спектре сигнала присутствует некоторое количество пиков и большая часть составляющих равна нулю, то становится возможно существенное сжатие информации, поскольку соответствующие пикам гармоники содержат практически всю информацию о характеристиках сигнала. Один из примеров использования сжатия динамического диапазона сигнала описан в [1]
Спектральный анализ оказывается полезным не только в радиотехнике. Использование преобразователей неэлектрических величин в электрические позволяет распространить использование анализа спектра сигнала на такие области как медицина, где выводы, сделанные в процессе обработки медицинских сигналов, помогают выявить диагностические признаки того или иного заболевания.
Как известно [2], любой периодический сигнал можно представить в виде комбинации гармонических колебаний. Совокупность амплитуд и частот гармоник, составляющих сигнал, называют спектром сигнала. Спектральный анализ основывается на преобразовании Фурье и заключается в том, что имеющийся сигнал разлагается на частотные или спектральные составляющие. В дальнейшем оцениваются спектральные характеристики сигнала – фаза, амплитуда, спектральная плотность мощности и другие.
Если характеристики сигнала в любой момент времени могут быть определены с вероятностью равной единице, то для изучения такого сигнала применяется гармонический анализ. Периодические сигналы можно разложить в ряд Фурье, а для непериодических используется интеграл Фурье. Примером описанного (детерминированного) сигнала может быть функция s(t), описывающая закон изменения напряжения между узлами цепи либо силы тока на участке цепи.
Преобразование Фурье определяется следующей функцией:
которую также называют спектральной плотностью сигнала. Сигнал в данном выражении определяется функцией f(t), а ω есть циклическая частота соответствующей составляющей сигнала.
Для периодической функции f(t) базисными функциями в преобразовании Фурье будут функции синуса и косинуса, поскольку . Тогда:
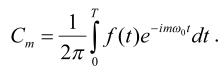 В этих выражениях циклическую частоту можно выразить через период сигнала: ω0 = 2π/Т.
В этих выражениях циклическую частоту можно выразить через период сигнала: ω0 = 2π/Т.
Если сигнал является случайным, то классический гармонический анализ для него провести нельзя, поскольку спектральные плотности на любой частоте не будут иметь конечных значений [3]. Тем не менее, гармонический анализ можно обобщить, усредняя средние разложения, которые были получены из отдельных выборок.
Рассмотрим некоторый стационарный случайный процесс, заданный функцией X(t). Для этого процесса будет справедлива теорема Винера-Хинчина, устанавливающая связь между корреляционной функцией R(τ) и энергетическим спектром сигнала F(ω) с помощью преобразований Фурье [4]:
 Функция F(ω) - это энергетический спектр стационарного случайного процесса, который позволяет проанализировать лишь усредненное распределение энергии сигнала по частотам, соответствующим элементарным гармоническим составляющим. При этом фазовая структура составляющих никак не учитывается и не может быть охарактеризована по функции F(ω). С физической точки зрения, величина F(ω) - это удельная мощность, которая приходится на спектральную составляющую сигнала в окрестности частоты ω. Очевидно, что физический смысл функция имеет лишь при положительных значениях частоты.
Функция F(ω) - это энергетический спектр стационарного случайного процесса, который позволяет проанализировать лишь усредненное распределение энергии сигнала по частотам, соответствующим элементарным гармоническим составляющим. При этом фазовая структура составляющих никак не учитывается и не может быть охарактеризована по функции F(ω). С физической точки зрения, величина F(ω) - это удельная мощность, которая приходится на спектральную составляющую сигнала в окрестности частоты ω. Очевидно, что физический смысл функция имеет лишь при положительных значениях частоты.
В программном пакете MathCad для практической реализации спектрального анализа используется алгоритм быстрого преобразования Фурье, который осуществляется через встроенные функции программы: fft(y) – вектор прямого преобразования Фурье, cfft(y) – вектор прямого комплексного преобразования Фурье и другие.
Осуществим прямое преобразование Фурье сигнала, заданного в виде следующей функции: 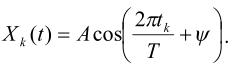 Параметры будем считать заданными: амплитуда сигнала А = 3, начальная фаза ψ = π/8, период сигнала Т = 100, а k = 0,1,…1023 – отсчеты времени. На рис. 1 представлено задание функции в среде MathCad.
Параметры будем считать заданными: амплитуда сигнала А = 3, начальная фаза ψ = π/8, период сигнала Т = 100, а k = 0,1,…1023 – отсчеты времени. На рис. 1 представлено задание функции в среде MathCad.
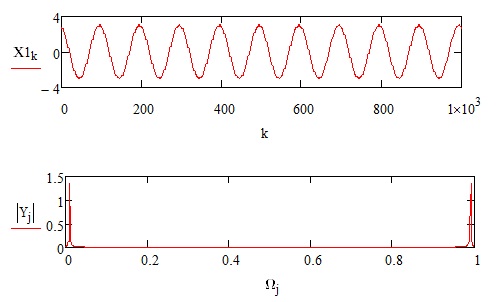
На рис. 2 приведены графики заданного сигнала и результат прямого преобразования Фурье.
Итак, численный анализ сигналов с помощью описанных выше формул можно проводить в программных пакетах MathCad, MathLab и других аналогичных пакетах. О практическом приложении полученных результатов сказано выше. Приведем некоторые примеры использования в радиотехнике при работе с речевыми сигналами. В [5] с помощью численного анализа спектральной характеристики сигнала в программе MathCad было определено минимальное время задержки в цифровом транспозиторе спектра сигнала, при котором сжатие фрагмента речевого сигнала происходит с минимальными искажениями. В [6] был проведен анализ математических моделей сигналов в прикладной программе MathLab, который позволил сделать выводы относительно возможностей компенсации помех акустической обратной связи в конференц-системах.
Анализ спектров отдельных звуков русского языка позволяет выявить некоторые способы распознавания слитной речи и построить алгоритмы перевода речевых сигналов в цифровые коды [7,8].
Также исследования амплитудно-частотной структуры речевого сигнала и его спектральных характеристик позволяют сформулировать частные критерии устойчивости, устанавливающие признаки начала процесса самовозбуждения электроакустических систем, ориентированных на усиление и воспроизведение речевых сигналов [9,10].
Библиографический список
- Галиев А.Л., Шишкина А.Ф. Устройство ослабления акустической обратной связи с компандированием огибающей речевого сигнала // Промышленные АСУ и контроллеры. – 2011. – № 6. – С. 48-50.
- В.И. Исаков. Статистическая теория радиотехнических систем. http://strts-online.narod.ru/
- П.В. Короленко, М.С. Маганова. Основы статистических методов в оптике. Учебное пособие. – М.: Изд-во Университетская книга, 2010, 164 с.
- В.Н. Бондарев, Г. Трестер, В.С. Чернега. Цифровая обработка сигналов: методы и средства. Учебн. пособие для вузов. 2-е изд. – X.: Изд-во Конус, 2001, 398 с.
- Шишкина А.Ф. Транспозитор спектра сигнала с минимальным временем задержки // Современные проблемы физики и математики: Труды Всероссийской научной конференции (16-18 сентября 2004 г., г. Стерлитамак)/Отв. ред. К.Б. Сабитов. – Уфа: Гилем, 2004. – Т. 2. – 203 с. – С. 200-203.
- Кондратьев К.В., Непомнящий О.В., Шишкина А.Ф., Сергеевич В.Н. Адаптивная компенсация помех обратного акустического тракта в процессе эксплуатации конференц-систем // Приборы и системы: управление, контроль, диагностика. – 2014. – № 3. – С. 53-59.
- Шишкина А.Ф., Антипин А.Ф. Способ цифрового анализа гласных звуков русского языка // Информационные технологии. Радиоэлектроника. Телекоммуникации (ITRT-2013): сб. ст. III международной заочной научно-технической конференции. / Поволжский гос. ун-т сервиса. – Тольятти: Изд-во ПВГУС, 2013. – 424 с. – С. 387-390.
- Антипин А.Ф., Шишкина А.Ф. Об одном пути решения проблемы автоматического распознавания речи // Информационные технологии. Радиоэлектроника. Телекоммуникации (ITRT-2012): сб. ст. II международной заочной научно-технической конференции. Ч. 1. / Поволжский гос. ун-т сервиса. – Тольятти: Изд-во ПВГУС, 2012. – 440 с. – С. 48-53.
- Шишкина А.Ф., Галиев А.Л., Галиева Р.Г. Частные критерии устойчивости электроакустических систем // Информационные технологии. Радиоэлектроника. Телекоммуникации (ITRT-2013): сб. ст. III международной заочной научно-технической конференции. / Поволжский гос. ун-т сервиса. – Тольятти: Изд-во ПВГУС, 2013. – 424 с. – С. 391-394.
- Галиев А.Л., Шишкина А.Ф. Лабораторный стенд для проведения экспериментов по оценке устойчивости локальных электроакустических систем // Информационные технологии. Радиоэлектроника. Телекоммуникации (ITRT-2012): сб. ст. II международной заочной научно-технической конференции. Ч. 1. / Поволжский гос. ун-т сервиса. – Тольятти: Изд-во ПВГУС, 2012. – 440 с. – С. 363-368.