Система массового обслуживания (СМО) представляет собой динамическую систему, используемую в условиях ограниченности ресурсов в целях быстрого обслуживания поступаемых заявок.
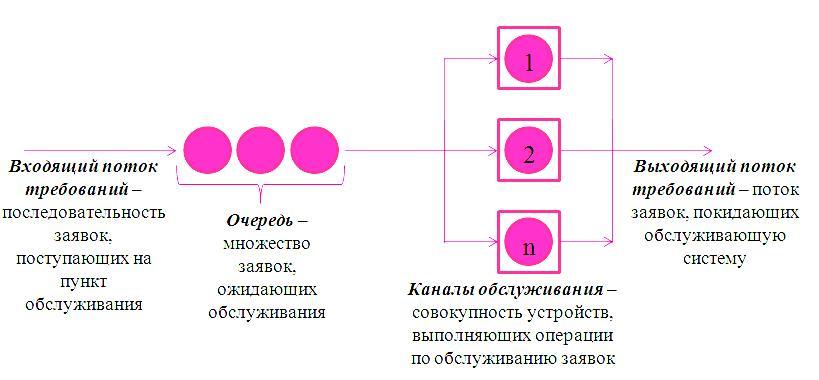
В общем случае СМО может быть представлена таким образом:
Рисунок 1- Схема СМО
При этом, если все каналы заняты, а заявки продолжают поступать, рассматривается СМО с ожиданием. Вновь поступаемые заявки могут обслуживаться последовательно и организованно, либо хаотично (учитывая преимущество одних заявок перед другими). Виды различных СМО приведены на рисунках 2-4.
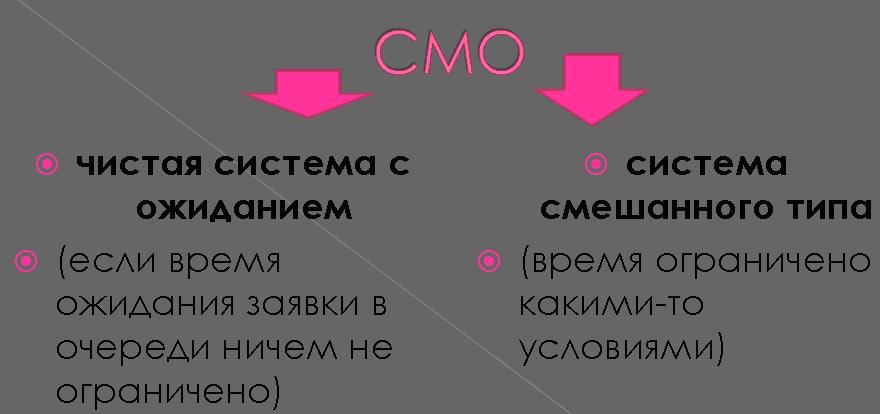
Рисунок 2- Виды СМО
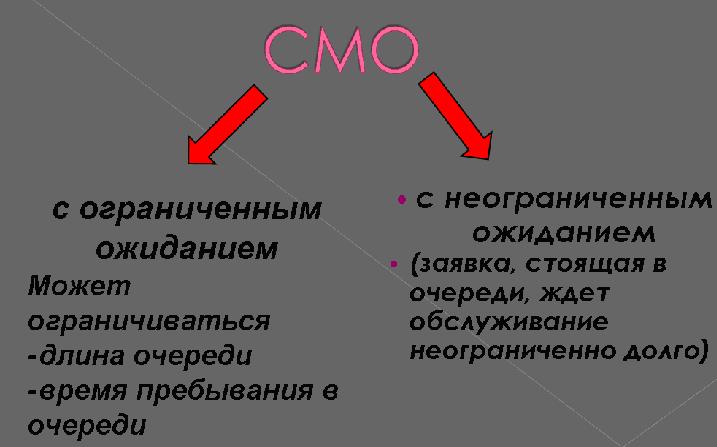
Рисунок 3- СМО в зависимости от условий ожидания
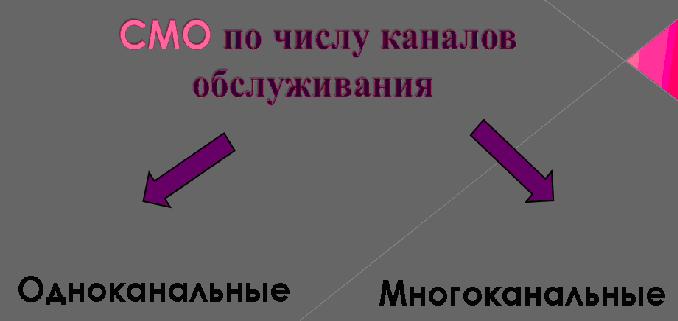
Рисунок 4- Виды СМО по числу каналов
Для одноканальных СМО с ожиданием рассматривают поток заявок с интенсивностью λ ; интенсивность обслуживания µ. При этом скорость обслуживания каналом заявок будет равна λ /μ .
Для ожидающих обслуживания заявок (канал обслуживания занят) выделяют СМО с ограниченным и неограниченным ожиданием (рисунок 5).
Рисунок 5- СМО с ограниченным и неограниченным ожиданием
При этом в зависимости от числа заявок, находящихся в системе могут использоваться следующие обозначения (рисунок 6):
Рисунок 6- Обозначения состояния каналов системы
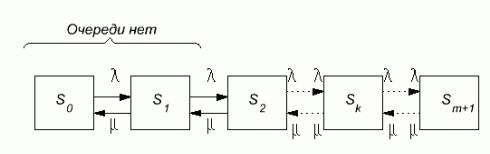
Рисунок 7- Система массового обслуживания с ожиданием (используется один канал)
Основными критериями эффективности функционирования СМО являются:
- вероятность немедленного обслуживания поступившей заявки;
- вероятность отказа в обслуживании поступившей заявки;
- пропускная способность СМО;
- доля заявок, получивших отказ в обслуживании;
- среднее время ожидания в очереди;
- средняя длина очереди и т.п.
Рассмотрим основные характеристики СМО на конкретном примере:
АЗС (с двумя колонками) обслуживает поток машин с интенсивностью = 0,8 (машин в минуту), среднее время обслуживания одной машины 2 мин. Рассчитать характеристики СМО, если конкуренции АЗС в рассматриваемом районе нет.
Рисунок 8- Расчет характеристик СМО
Таким образом, анализ СМО позволяет оптимизировать работу системы и эффективно регулировать обслуживание поступаемых заявок.
Библиографический список
- Гармаш А.Н., Орлова И.В. Математические методы в управлении: учебное пособие. – М.: Вузовский учебник, 2011.
- Математические методы в управлении: Компьютерный практикум и методические указания по выполнению лабораторной работы для магистрантов первого года обучения, направление 080500.68 «Магистр менеджмента». Части 1, 2 / А.Н. Гармаш, И.В. Орлова, Е.Н. Горбатенко, В.А. Большаков. – М.: ВЗФЭИ, 2011.
- Федосеев В.В., Гармаш А.Н., Орлова И.В. Экономико-математические методы и прикладные модели: учебное пособие для вузов. – 3-е изд. – М.: Юрайт-издат : Высшее образование, 2011.