Уравнения Нильсена
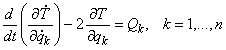 , (1)
, (1)будучи менее известными, чем уравнения Лагранжа, столь же быстро как последние (а для систем со многими степенями свободы ещё быстрее) позволяют получить дифференциальные уравнения движения несвободной механической системы, пригодные для последующего аналитического либо численного интегрирования.
Здесь: T – кинетическая энергия системы, qk – k-я обобщенная координата, Qk – обобщенная сила, соответствующая k-й обобщенной координате, n – число степеней свободы системы.
Рассмотрим механическую систему с одной степенью свободы, кинетическая энергия которой определяется выражением:
где A(q) – коэффициент инерции системы, ![]() – обобщённая скорость.
– обобщённая скорость.
Вычислим производные, входящие в уравнение (1):
Подставляя выражения (2) в формулу (1), получаем дифференциальное уравнение движения механической системы:
 |
|
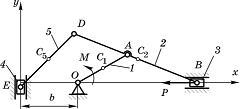
Рис. 1 Схема плоского механизма с одной степенью свободы
|
В качестве учебного примера рассмотрим механизм, представленный на рис. 1. Кривошип OA длины l1=0,3 м и массы m1=2 кг вращается вокруг оси, перпендикулярной плоскости чертежа и проходящей через точку O, под действием постоянного вращающего момента M=20 Н·м. К ползуну B приложена сила вязкого сопротивления ![]() , модуль которой прямо пропорционален скорости движения ползуна
, модуль которой прямо пропорционален скорости движения ползуна ![]() , где
, где ![]() =1,5 Н·м/с коэффициент вязкого сопротивления,
=1,5 Н·м/с коэффициент вязкого сопротивления, ![]() скорость ползуна B. Массы всех звеньев (mBD=m2=5 кг; mB=m3=1 кг; mE=m4=1 кг; mDE=m5=2,5 кг) и их размеры (lAB=l21=0,4 м; lAD=l22=0,5 м; lDE=l5=0,5 м, b=0,3 м) считаются известными. Механизм расположен в вертикальной плоскости. Ползуны 3 и 4 считать материальными точками, а звенья 1, 2 и 5 однородными тонкими стержнями. Силы трения в подвижных соединениях не учитываются. В начальный момент времени (t=0) известны положение и угловая скорость ведущего звена:
скорость ползуна B. Массы всех звеньев (mBD=m2=5 кг; mB=m3=1 кг; mE=m4=1 кг; mDE=m5=2,5 кг) и их размеры (lAB=l21=0,4 м; lAD=l22=0,5 м; lDE=l5=0,5 м, b=0,3 м) считаются известными. Механизм расположен в вертикальной плоскости. Ползуны 3 и 4 считать материальными точками, а звенья 1, 2 и 5 однородными тонкими стержнями. Силы трения в подвижных соединениях не учитываются. В начальный момент времени (t=0) известны положение и угловая скорость ведущего звена:![]() и
и ![]() с-1.
с-1.
Рассматриваемый механизм имеет одну степень свободы. За обобщённую координату примем угол поворота 1 кривошипа ОА.
Разобьем механизм на три части (подсистемы): а) звено 1 (рис. 2), б) звенья 2-3 (рис. 3), в) звенья 4-5 (рис. 4). Для каждой из подсистем выберем обобщенные координаты.
 |
 |
|
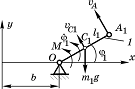
Рис. 2 Схема подсистемы механизма, состоящей из звена 1
|
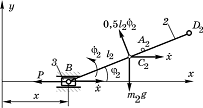
Рис. 3 Схема подсистемы механизма, состоящей из звеньев 2-3
|
Подсистема а стержень 1, обобщенная координата 1.
Подсистема б звенья 2 и 3, обобщенные координаты x и 2.
Подсистема в звенья 4 и 5, обобщенные координаты y и 5.
 |
|
Рис. 4 Схема подсистемы, состоящей из звеньев 4-5
|
Обобщённую координату 1 будем называть основной, а остальные (![]() ) – избыточными. Для определения избыточных координат составим уравнения связей.xА1=xА2,
) – избыточными. Для определения избыточных координат составим уравнения связей.xА1=xА2, ![]() yА1=yА2,
yА1=yА2, ![]()
xD2=xD5, ![]() yD2=yD5,
yD2=yD5, ![]()
Систему уравнений (4)-(7) запишем в матричной форме:
где
.gif) ;
;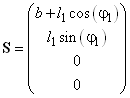 .
.
Решение матричного уравнения (8) проведём при помощи математического пакета Mathcad и получим начальные значения избыточных координат при заданной сборке механизма:
Продифференцируем уравнение (8) по основной обобщённой координате и получим матричное уравнение, из которого можно определить значения аналогов скоростей (впервые были использованы Л.В. Ассуром) для избыточных обобщённых координат:
где
.gif) – матрица Якоби;
– матрица Якоби; .gif) ;
;
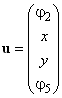 – матрица избыточных обобщённых координат;
– матрица избыточных обобщённых координат;.gif) – матрица аналогов избыточных обобщённых скоростей (штрихами обозначены частные производные от избыточных координат по основной координате 1).
– матрица аналогов избыточных обобщённых скоростей (штрихами обозначены частные производные от избыточных координат по основной координате 1).
Если матрица Якоби не особенна, то из уравнения (9) находим матрицу аналогов скоростей:
В результате вычислений в программе Mathcad получаем следующие начальные значения начальных избыточных обобщённых скоростей:
Избыточные обобщённые скорости связаны с аналогами скоростей формулами:
Эти соотношения можно записать в матричной форме:
Здесь: .gif) – избыточные обобщённые скорости системы.
– избыточные обобщённые скорости системы.
Аналогично, вычислив производную от выражения (9) по основной обобщённой координате 1, получим уравнение
где
.gif) ;
; 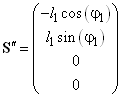 ;
; .gif) .
.
Из уравнения (13) определим матрицу аналогов ускорений:
Избыточные обобщённые ускорения связаны с аналогами скоростей и ускорений формулами:
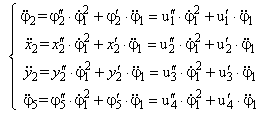 . (14)
. (14)Эти соотношения можно записать в матричной форме:
где .gif) – избыточные обобщённые ускорения системы.
– избыточные обобщённые ускорения системы.
На следующем этапе решения задачи для каждой из подсистем составим выражения для кинетической энергии.Кинетическая энергия кривошипа 1:
Кинетическая энергия звеньев, входящих в подсистему б:
Кинетическая энергия звеньев, входящих в подсистему в:
Кинетическая энергия всей системы с учётом соотношений (10) и (11) принимает вид:
где ![]()
– коэффициент инерции системы.
В дифференциальное уравнение (3) входит производная ![]() :
:
Сообщим кривошипу ОА возможную скорость ![]() и определим сумму мощностей внешних сил, действующих на механизм:
и определим сумму мощностей внешних сил, действующих на механизм:
Отсюда следует выражение для обобщённой силы Q:
Подставляя выражения (16)-(18) в уравнение (3), получаем дифференциальное уравнение:
Отсюда нетрудно выразить угловое ускорение ведущего звена механизма:
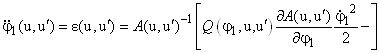 .
.Приведём полученную систему дифференциальных уравнений к нормальному виду и подготовим её к численному интегрированию методом Рунге-Кутты в пакете Mathcad (разумеется, для численного решения задачи можно использовать любой из существующих математических пакетов программ; в рассматриваемом случае пакет Mathcad применен в качестве примера).
Для этого создадим матрицу начальных значений фазового вектора:
и, следуя алгоритму интегрирования системы дифференциальных уравнений, зашитому в пакете Mathcad, сформируем вектор-столбец правых частей этой системы:
Для решения задачи используем процедуру численного интегрирования системы дифференциальных уравнений методом Рунге-Кутты с фиксированным шагом:
Результаты расчетов представим в виде хронограмм обобщенных координат и обобщенных скоростей.
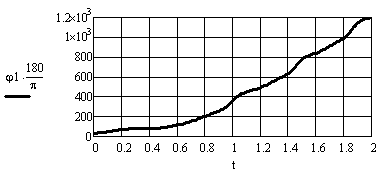
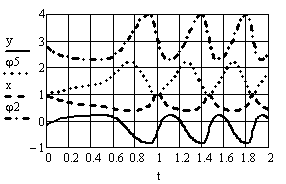
На рис. 5 и 6 показаны хронограммы обобщённых координат (основной и избыточных), а также угловой скорости и углового ускорения ведущего звена механизма.
  |
|
Рис. 5 Зависимости основной и избыточных обобщённых координат от времени
|
  |
|
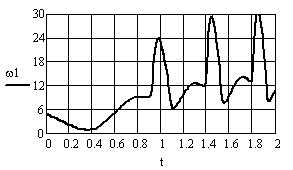
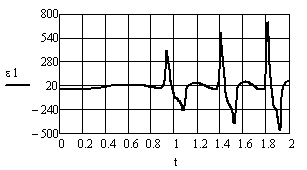
Рис. 6 Зависимости угловой скорости 1 и углового ускорения e1 ведущего звена от времени
|
Для получения хронограмм внутренних усилий в шарнирных соединениях механизма требуется рассмотреть движение подсистем ОА1, BD2 и ED5.
Библиографический список
- Доронин Ф.А., Доев В.С. Исследование движения плоского механизма с помощью пакета Mathcad. // Теория механизмов и машин. 2011. №1(17). С. 77-87.
- Зиборов К.А. Силовой анализ механизмов с помощью программы Mathcad. / Зиборов К.А., Мацюк И.Н., Шляхов Э.М. // Теория механизмов и машин. 2010. №1(15). С. 83-88.
- Мацюк И.Н., Шляхов Э.М. Кинетостатика плоских стержневых механизмов произвольной структуры // Теория механизмов и машин. 2013. №1(21). Том 11. С. 71-77.
- Мкртычев О.В. Компьютерное моделирование при силовом расчёте плоских механизмов. // Теория механизмов и машин. 2013. №1(21). Том 11. С. 77-84.
- Мацюк И.Н., Шляхов Э.М. Принцип возможных перемещений в исследовании механизмов.// Теория механизмов и машин. 2014. №1(23). С. 51-58.
- Доев В.С., Доронин Ф.А. Сборник заданий по теоретической механике на базе Mathcad: Учебное пособие. СПб.: Издательство «Лань», 2010. 592 с.
- Елисеев В.В. О рамках специальности «Теория механизмов и машин»// Теория механизмов и машин. 2009. №1(17). С. 60-63.
