Адаптивные фильтры являются неотъемлемой частью многих технических систем, где требуется восстановление сигнала от искажений, оценка параметров модели, управление в условиях неопределенности и нестационарности. Без адаптивной фильтрации совершенно невозможна высокоскоростная передача сигналов, мобильная связь, радиолокация, современная медицинская техника [1-4].
Алгоритмы адаптации для цифровых фильтров – значительная и сформировавшаяся область исследований, представление о которой дают монографии отечественных и зарубежных авторов [1,2].
В настоящей работе предлагается рекурсивный алгоритм для идентификации весовых коэффициентов линейного сумматора, который отличается тем, что инверсия матрицы наблюдений вычисляется рекурсивно с квадратичной вычислительной сложностью одной итерации. Приведено доказательство рекурсивных соотношений, на которых основано итеративное вычисление инверсии матрицы наблюдений. С помощью MATLAB продемонстрировано применение разработанного алгоритма к идентификации цифрового КИХ-фильтра со смещением по выходу и нестационарными параметрами.
Обратная свертка как метод идентификации
Пусть – значение сигнала в дискретный момент времени k. Если
— вектор весовых коэффициентов, то выход КИХ-фильтра порядка
определяется сверткой:
(1)
В данной работе мы обобщим объект исследования, устранив зависимость элементов друг от друга и подразумевая что сумма (1) вычисляется от независимых переменных
, которые могут быть, например, попарно ортогональными функциями. В результате получаем многоканальный линейный сумматор:
или
где понимается как значение входной переменной
в момент времени
, а
– вектор значений входов в момент
.
Рассмотрим квадратную матрицу следующего вида
,
которую будем называть матрицей наблюдений.
Как видно, вектор весов однозначно определяется решением матричного уравнения
, (2)
где – вектор текущего и предыдущих значений выхода.
Решение уравнения (2) единственно только если матрица не вырождена:
.
Это требование известно как условие неисчезающего возбуждения (persistent excitation). Применительно к КИХ-фильтрам, процедура решения уравнения (2) называется обратной сверткой или деконволюцией.
Рекуррентные соотношения для вычисления обратной свертки
В этом разделе мы покажем как уравнение (2) может быть решено без использования инверсии матрицы для
.
Определим матрицу
и вектор
.
Легко видеть, что
, (3)
поскольку (3) – это все равно что уравнение (2), домноженное слева и справа на .
Теорема 1. Пусть для момента времени известны
и
. Тогда для момента времени
и текущего вектора входов
верны следующие рекуррентные соотношения:
, (4.1)
. (4.2)
Доказательство.
Для начала заметим, что матица может быть представлена как конкатенация вектор-стобцов
.
Докажем (4.2). По определению , можно записать следующее
,
.
Вычитая , сразу получаем (4.2):
.
Аналогично можно доказать (4.1). Для этого заметим, что
.
Отсюда, раскрывая скалярное произведение векторов, получаем
,
одновременно с этим
.
Вычитая , сразу получаем (4.1):
.
Доказательство закончено.
Рекурсивный алгоритм
Соотношения (4) является основой рекурсивного алгоритма идентификации. Введем в рассмотрение дополнительную матрицу
, (5.1)
. (5.2)
Применив к (5) матричное тождество Вудбери [1], получаем
, (6.1)
. (6.2)
Таким образом, задав для
, можно вычислить с помощью рекуррентных соотношений (6) все
без необходимости обращения матрицы
. Отсюда, одна итерация алгоритма имеет вычислительную сложность, определяемую только сложностью перемножения матриц, т.е.
в худшем случае, что существенно лучше вычисления инверсии
, которая занимает
вычислительных операций.
Алгоритм на каждой итерации по текущему вектору входов
вычисляет
по (6), также на основе (4.2) по
вычисляется
, далее осуществляется расчет оценки весовых коэффициентов
, после чего происходит переход к новой итерации
и сохраняются новые значения
и
.
Пример применения метода
Для демонстрации возможности алгоритма рассмотрим простой вычислительный пример идентификации параметров КИХ-фильтра второго порядка с медленно меняющимися коэффициентами и смещением на выходе
:
Каждую итерацию коэффициенты изменяются следующим образом: , где
– общее количество итераций моделирования алгоритма,
.
В качестве начальных значений весовых коэффициентов выбраны . Работа алгоритма моделировалась в течение
итераций. В качества источника тестового входного сигнала
использовался генератор псевдослучайных чисел, равномерно распределенных на интервале [0, 10].
Для проверки устойчивости алгоритма к зашумленным данным к значениям выходной переменной был добавлен аддитивный шум амплитудой 0.1.
На рисунке 1 приведены входной и выходной сигнал системы. На рисунке 2 показаны идентифицированные оценки параметров (зеленым цветом) вместе с их истинными значениями (синим цветом).
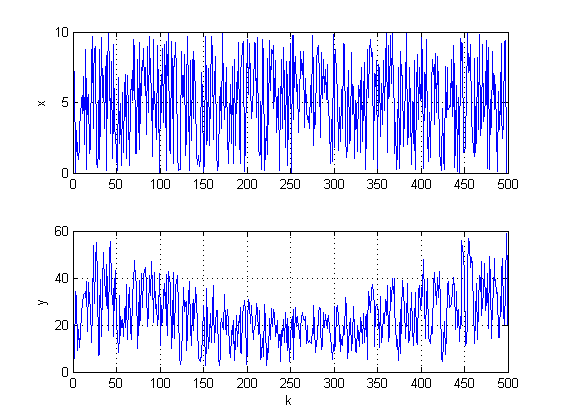
Рисунок 1 – Входной сигнал и отклик системы.
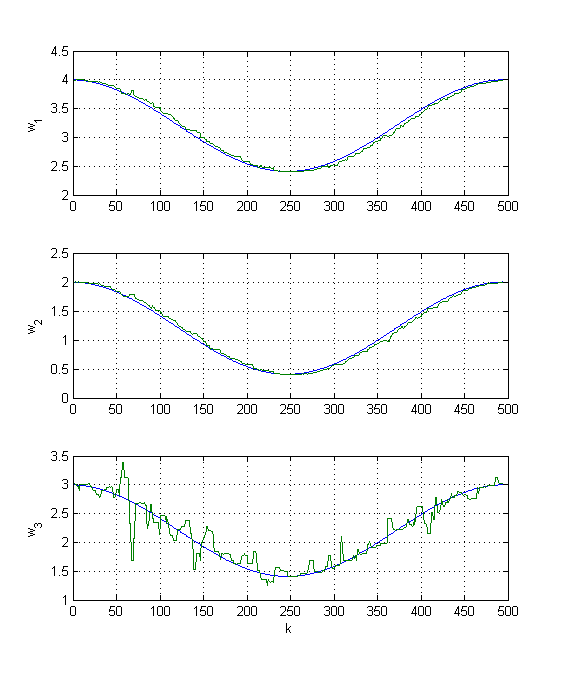
Рисунок 2 – Весовые коэффициенты и их идентифицированные оценки.
Как видно из результатов моделирования, алгоритм численно устойчив и показывает удовлетворительную точность идентификации ошибок.
Заключение
В настоящей работе был предложен и проанализирован метод идентификации параметров линейного взвешенного сумматора, основанный на рекурсивном вычислении инверсии матрицы наблюдений. Итерация алгоритма имеет квадратичную вычислительную сложность. При этом алгоритм полностью эквивалентен по результату методу обратной свертки (деконволюции) с фиксированным скользящим окном. Работоспособность метода продемонстрирована на примере КИХ-фильтра с медленно меняющимися коэффициентами и смещением на выходе.
Дальнейшая работа будет сосредоточена на применении разработанного алгоритма к реальным техническим задачам, а именно идентификации параметров модели литий-ионных аккумуляторов для оценки состояния заряда и контроля годности батареи [5]. Также алгоритм будет реализован программно для процессора цифровой обработки сигналов.
В заключение, стоит сказать, что программная реализация алгоритма в MATLAB можно скачать в архиве по ссылке
https://sites.google.com/site/akpc806a/Matlab_RLS_2.rar
Библиографический список
- Widrow B., Walach E. Adaptive Inverse Control, Reissue Edition: A Signal Processing Approach. – John Wiley & Sons, 2008. – 508 pp.
- Джиган В. И. Адаптивная фильтрация сигналов: теория и алгоритмы – М.: Техносфера, 2013. – 528 с
- Джиган В. И. Адаптивные антенные решетки для систем цифровой связи: проблемы и их решение //Всероссийская научно-техническая конференция” Проблемы разработки перспективных микро-и наноэлектронных систем (МЭС)”. Сборник трудов. – Институт проблем проектирования в микроэлектронике РАН, 2008. – №. 1.
- Ribeiro R. A., Serralheiro A. J., Piedade M. S. Application of Kalman and RLS adaptive algorithms to non-linear loudspeaker controller parameter estimation: a case study //Acoustics, Speech, and Signal Processing, 2005. Proceedings.(ICASSP’05). IEEE International Conference on. – IEEE, 2005. – Т. 3. – С. iii/145-iii/148 Vol. 3.
- Борисевич А.В. Подход к адаптивному оцениванию напряжения холостого хода литий-ионных аккумуляторов в динамическом режиме // Оптимизация производственных процессов – Севастополь:Изд-во СевНТУ, 2014 – Выпуск 15/2014 – С. 149-153
