В современном мире человек каждый день сталкивается с проблемой выбора. Причем выбор осложняется рассмотрением множества альтернатив. Где получать образование или работать, как поступать в том или ином случае, даже обычная покупка ставит обывателя в затруднительное положение. Причем, последний случай осложняется еще и субъективной оценкой предмета выбора: советы продавцов или знакомых людей, цвет покупки, размер и, в большинстве случаев, цена сбивают с толку и зачастую заставляют покупателя останавливаться совсем не на том варианте. Именно для решения подобных проблем выбора и существуют различные методы принятия решений.
Объектом исследования является выбор одного из пяти планшетных компьютеров: Samsung Galaxy Tab 2 7.0 P3110 8Gb, ViewSonic ViewPad 10e, Lenovo IdeaTab A1000 16Gb, ASUS Google Nexus 7 32Gb и Apple iPad mini 16Gb.
В данной статье рассматривается критерий Парето, он же Принцип Парето, являющийся наиболее оптимальным для решения многокритериальной задачи выбора. Примерами подобного утверждения служат различные исследования и частные применения принципа Парето. Так, В.В.Подинский, В.Д.Ногин [1] подробно изложили применение метода для решения многокритериальных задач. А.С.Винокуров и др. [2, 3], Шуршев В.Ф. и Л.В.Буй [4] применяли критерий Парето для решения частных задач, подробно расписывая ход решения, чем доказали его оптимальность для применения в повседневной жизни. Р.Кох [5] раскрыл важность Принципа 80/20, или принципа Парето, для его применения в среде финансов. Этот же критерий возможен и для применения к задачам прикладной математики, что доказали А.В.Богданова и В.Д.Ногин [6]. Р.И.Баженов и др. [7-13] применяли многокритериальные методы выбора решений в практике обучения студентов. А.А.Наумов и Р.Баженов исследовали применимость метода нормализации критериев решения многокритериальных задач оптимизации [14-17]. А.Афанасьев [18] и М.С.Гоерес [19] применяли метод Парето в различных областях.
В ходе исследования были выбраны критерии для сравнения: емкость аккумулятора, процессор, размер оперативной памяти, встроенная память, разрешение экрана [20].
Обозначим множество альтернатив планшетов A={ai}, i=1,2, 3,…,n, где ai – планшеты, выбранные по критериям; ai={ej}, j=1,2, 3,…,m , где ej – показатели качества a [21].
В качестве модели данных используется реляционное отношение для описания вариантов на множестве A (табл.1).
Таблица 1 – Критерии для применения критерия Парето
|
Альтернатива
|
Показатели альтернатив ej и их значения
|
||||
| e1 Емкость аккумулятора ^ |
e2 Производительность процессора ^ |
e3 Размер оперативной памяти ^ |
e4 Встроенная память ^ |
e5 Разрешение экрана ^ |
|
| a1 Samsung Galaxy Tab 2 7.0 P3110 8Gb |
4000 мАч
|
1000 МГц
|
1 Гб
|
8 Гб
|
1024х600
|
| a2 ViewSonic ViewPad 10e |
5400 мАч
|
1000 МГц
|
512 Мб
|
4 Гб
|
1024х768
|
| a3 Lenovo IdeaTab A1000 16Gb |
3500 мАч
|
1200 МГц
|
1 Гб
|
16 Гб
|
1024х600
|
| a4 ASUS Google Nexus 7 32Gb |
3950 мАч
|
1,5 ГГц
|
2 Гб
|
32 Гб
|
1920х1200
|
| a5 Apple iPad mini 16Gb |
4430 мАч
|
1000 МГц
|
512 Мб
|
16 Гб
|
1024х768
|
В названии показателей указывается их направленность: ^ – направленность на максимум, v – направленность на минимум. В данной статье все показатели исследуются на максимум.
Показатели качества {ej}, j=1,2, 3,…,m вариантов A={ai} описываются их значениями {ei,j} по строкам.
Фундаментом алгоритма выбора по принципу Парето служит модель, основанная на описании множеств возможных вариантов с помощью фактор-множества F(A/e), которым являются множества окрестностей единичного радиуса, взятых для всех ai ![]()
![]() A, i=1,2, 3,…,n. При этом окрестность Oi элемента ai – это множество элементов {ai*}, доминирующих или эквивалентных ai (ai* >= ai) [21].
A, i=1,2, 3,…,n. При этом окрестность Oi элемента ai – это множество элементов {ai*}, доминирующих или эквивалентных ai (ai* >= ai) [21].
Для решения проблемы необходимо построить ассоциативные матрицы линейного порядка по показателю качества в виде реляционного отношения:
L(A/e) = <ai+1, ai,…, an>, i=1,2, 3,…,n, ai+1 > ai по ej, j=1,2, 3,…,m.
Если альтернатива ai доминирует альтернативу ak, то элемент ассоциативной матрицы dji,k принимает значение 1, иначе элемент dji,k принимает значение 0. Если альтернативы ai, ak несравнимы по показателю качества, то элементы dji,k = djk,i = 1. Элементы, расположенные на главной диагонали ассоциативной матрицы всегда принимают значение 0. Отсюда следует, что:
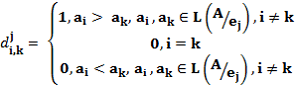
На основе поставленных условий производится построение линейных порядков по e1, e2, e3, e4, e5, после чего осуществляется построение ассоциативных матриц (табл.2-6):
L(A/e1) = {a1, a2, a3, a4, a5}
L(A/e2) = {{a1, a2, a5}, a3, a4}
L(A/e3) = {{a1, a3}, {a2, a5}, a4}
L(A/e4) = {a1, a2, {a3, a5}, a4}
L(A/e5) = {{a1, a3}, {a2, a5}, a4}
Таблица 2 – Ассоциативная матрица АсМ1 фактор-множества F(A/e1) линейного порядка L(A/e1)
| Альтернатива | Окрестность | ||||
| O1(a1/e1) | O2(a2/e1) | O3(a3/e1) | O4(a4/e1) | O5(a5/e1) | |
| a1 | 0 | 1 | 1 | 1 | 0 |
| a2 | 1 | 0 | 1 | 1 | 1 |
| a3 | 1 | 1 | 0 | 0 | 0 |
| a4 | 1 | 1 | 1 | 0 | 0 |
| a5 | 1 | 1 | 1 | 1 | 0 |
Таблица 3 – Ассоциативная матрица АсМ2 фактор-множества F(A/e2) линейного порядка L(A/e2)
| Альтернатива | Окрестность | ||||
| O1(a1/e2) | O2(a2/e2) | O3(a3/e2) | O4(a4/e2) | O5(a5/e2) | |
| a1 | 0 | 0 | 0 | 0 | 1 |
| a2 | 0 | 0 | 0 | 0 | 1 |
| a3 | 1 | 1 | 0 | 0 | 1 |
| a4 | 1 | 1 | 1 | 0 | 1 |
| a5 | 0 | 0 | 0 | 0 | 0 |
Таблица 4 – Ассоциативная матрица АсМ3 фактор-множества F(A/e3) линейного порядка L(A/e3)
| Альтернатива | Окрестность | ||||
| O1(a1/e3) | O2(a2/e3) | O3(a3/e3) | O4(a4/e3) | O5(a5/e3) | |
| a1 | 0 | 1 | 1 | 0 | 1 |
| a2 | 0 | 0 | 0 | 0 | 1 |
| a3 | 1 | 1 | 0 | 0 | 1 |
| a4 | 1 | 1 | 1 | 0 | 1 |
| a5 | 0 | 1 | 0 | 0 | 0 |
Таблица 5 – Ассоциативная матрица АсМ4 фактор-множества F(A/e4) линейного порядка L(A/e4)
| Альтернатива | Окрестность | ||||
| O1(a1/e4) | O2(a2/e4) | O3(a3/e4) | O4(a4/e4) | O5(a5/e4) | |
| a1 | 0 | 1 | 0 | 0 | 0 |
| a2 | 0 | 0 | 0 | 0 | 0 |
| a3 | 1 | 1 | 0 | 0 | 1 |
| a4 | 1 | 1 | 1 | 0 | 1 |
| a5 | 1 | 1 | 1 | 0 | 0 |
Таблица 6 – Ассоциативная матрица АсМ5 фактор-множества F(A/e5) линейного порядка L(A/e5)
| Альтернатива | Окрестность | ||||
| O1(a1/e5) | O2(a2/e5) | O3(a3/e5) | O4(a4/e5) | O5(a5/e5) | |
| a1 | 0 | 0 | 1 | 0 | 0 |
| a2 | 1 | 0 | 1 | 0 | 1 |
| a3 | 1 | 0 | 0 | 0 | 0 |
| a4 | 1 | 1 | 1 | 0 | 1 |
| a5 | 1 | 1 | 1 | 0 | 0 |
Результирующая матрица АсМрез строится на основании ассоциативных матриц АсМ1, АсМ2, АсМ3, АсМ4 и АсМ5, путем пересечения фактор-множеств по каждому из показателей. Элементы матрицы АсМрез определяются по следующей формуле:
![]()
Таблица 7 – Результирующая матрица АсМрез
| Альтернатива | Окрестность | ||||
| O1(a1) | O2(a2) | O3(a3) | O4(a4) | O5(a5) | |
| a1 | 0 | 0 | 0 | 0 | 0 |
| a2 | 0 | 0 | 0 | 0 | 0 |
| a3 | 1 | 0 | 0 | 0 | 0 |
| a4 | 1 | 1 | 1 | 0 | 0 |
| a5 | 0 | 0 | 0 | 0 | 0 |
В результате построения матрицы АсМрез некоторые окрестности Оh(ah/{e1, e2,…,en}) могут принимать нулевое значение для всех альтернатив:
![]()
Тогда во множество оптимальных вариантов включается альтернатива ah и используется метод удаления столбцов и строк из результирующей матрицы.
В данном случае матрица АсМрез(табл.7) содержит окрестности О4 и О5 с результатами Z4=Z5=0, из чего следует, что альтернативы а4 и а5 являются наихудшими вариантами и подлежат удалению для последующего исследования оставшихся вариантов.
Таблица 8 – Результирующая матрица АсМрез после удаления наихудших альтернатив а4 и а5
|
Альтернатива
|
Окрестность | ||
| O1(a1) | O2(a2) | O3(a3) | |
| a1 | 0 | 0 | 0 |
| a2 | 0 | 0 | 0 |
| a3 | 1 | 0 | 0 |
После удаления столбцов окрестностей О4(а4) и О5(а5) получается новая результирующая матрица (табл.8) и подвергается дальнейшему исследованию.
Таблица 9 – Результирующая матрица АсМрез после удаления наихудших альтернатив а2 и а3
|
Альтернатива
|
Окрестность |
| O1(a1) | |
| a1 | 0 |
Результатом исследования является построение отношения порядка
<{a4, a5}, {a2, a3}, a1> ,
которое показывает очередность рассмотренных альтернатив от наихудшего (в данном случае – наихудших) к оптимальному, которым является a1 - планшетный компьютер Samsung Galaxy Tab 2 7.0 P3110 8Gb.
Основанный на бинарных отношениях и алгебре множеств, изучаемых в школьном курсе информатики и математики, Критерий Парето достаточно прост в применении, так как не требует сложных вычислений и построения многоярусных формул. Этим он и привлекателен для большинства людей, стоящих перед проблемой выбора и не умеющих применять различные методы принятия решений на практике, более того, даже не знакомых с ними.
Библиографический список
- Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. М.: Наука, 1982. 255 с.
- Винокуров А.С., Белов И.В., Баженов Р.И. Использование критерия Парето для принятия оптимального решения по выбору цифрового фотоаппарата // Современная техника и технологии. 2014. № 10 [Электронный ресурс]. URL: http://technology.snauka.ru/2014/10/4660
- Винокуров А.С., Баженов Р.И. Использование метода анализа иерархий для принятия оптимального решения по выбору цифрового фотоаппарата // Современная техника и технологии. 2014. № 9 (37). С. 11-17.
- Шуршев В.Ф., Буй Л.В. Использование критерия Парето при рациональном выборе сканирующих приемников и трансиверов // Вестник Астраханского Государственного Технического Университета. Серия: управление, вычислительная техника и информатика. 2014. №1. С. 112-120.
- Koch R. The 80/20 principle: the secret to achieving more with less. Random House LLC, 2011.
- Богданова А.В., Ногин В.Д. Сужение множества Парето на основе простейших наборов нечеткой информации об относительной важности критериев // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. 2007. № 2. С. 1-17.
- Баженов Р.И. О методике преподавания метода анализа иерархий в курсе «Информационная безопасность и защита информации» // Современные научные исследования и инновации. 2014. №4 (36). С. 76.
- Баженов Р. И. Информационная безопасность и защита информации: практикум. Биробиджан: Изд-во ГОУВПО «ДВГСГА», 2011. 140 с.
- Vexler V.A., Bazhenov R.I., Bazhenova N.G. Entity-relationship model of adult education in regional extended education system // Asian Social Science. 2014. Т.10. №20. С.1-14.
- Баженов Р.И. Проектирование методики обучения дисциплины «Информационные технологии в менеджменте» // Современная педагогика. 2014. №8(21). С. 24-31.
- Баженов Р.И. О методике обучения проектированию информационных систем будущих менеджеров // Психология, социология и педагогика. 2014. № 8 (35). С. 30-38.
- Баженов Р.И. Об организации научно-исследовательской практики магистрантов направления «Информационные системы и технологии» // Современные научные исследования и инновации. 2014. № 9-2 (41). С. 62-69.
- Баженов Р.И. О методике преподавания дисциплины «Управление проектами информационных систем» // Современные научные исследования и инновации. 2014. № 3 (35). С. 55.
- Наумов А.А. К проблемам метода нормализации критериев в задачах векторной оптимизации // Theoretical & Applied Science. 2013. № 8 (4). С. 24-27.
- Наумов А.А. К S_P-неустойчивости метода нормализации критериев решения многокритериальных задач оптимизации // Theoretical & Applied Science. 2013. № 9. С. 14-17.
- Наумов А.А. К свойству S_P-инвариантности методов решения многокритериальных задач оптимизации // Theoretical & Applied Science. 2013. № 10 (6). С. 1-4.
- Наумов А.А., Баженов Р.И. О неустойчивости метода нормализации критериев // Современные научные исследования и инновации. 2014. № 11 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/11/40408 (дата обращения: 10.11.2014).
- Afanasiev A. Pareto-efficiency, cost minimisation, and innovations: the key Gazprom policies targeting gas production // GAS Industry of Russia. 2009. № 3. С. 30-37.
- Goeres M. Revisiting Pareto: A Re-analysis of the Specific Requirements of Pareto’s Law: дис. Nova Southeastern University, 2005.
- Кардаш А.С., Винс А.А., Баженов Р.И. Об оптимальном выборе планшетного компьютера для младшего школьника // Современная техника и технологии. 2014. №10 [Электронный ресурс]. URL: http://technology.snauka.ru/2014/10/4712 (дата обращения: 10.11.2014).
- Лотов А.В., Поспелова И.И. Многокритериальные задачи принятия решений: Учебное пособие. М.: Макс Пресс, 2008. 197 с.


