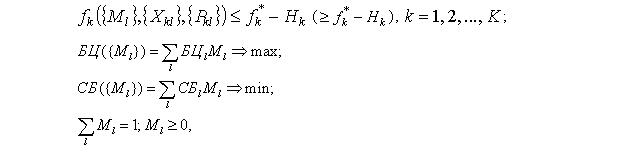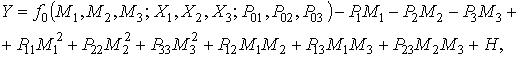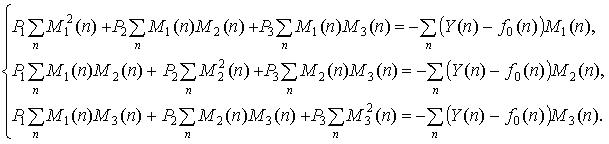Под смесью понимается система, состоящая из нескольких компонентов, которые являются независимыми и не вступающими в реакции физической и химической природы, в результате которых бы менялись массовые доли исходных компонентов или  образовывались новые компоненты. В качестве пищевой смеси в дальнейшем рассмотрим мясной фарш.

В целях управления качеством смеси, рассматривается ее модель.В общем случае задают некоторую модель смеси. Так, если  X_kl– k-я характеристика l-го компонента (k=1,…K; l=1,..,L ), а  M_l– массовая доля l-ого компонента , то k-я характеристика смеси может быть записана в виде аддитивной стохастической модели [1]

                                            (1)

где  – неизвестная функциональная зависимость с параметрами P_kl;  H_k– ошибка или погрешность вычислений, показывающая величину отклонения расчетных значений от эмпирических данных. Тогда модель оптимизации смеси, будет определяться следующими ограничениями:

  (2)

 где  ‑ граничные значения характеристик смеси, которые устанавливаются экспериментально или пользуясь соответствующей нормативной документацией;    – функциональные критерии (биологическая ценность и себестоимость l-го компонента соответственно).

Модель (1) может быть представлена следующими видами:

1)              (3)

где  Y ‑ измеряемая физическая величина.

Это модель смеси, в состав которой входит  большое число компонентов различных L типов , которые могут взаимодействовать.

2)        (4)

Это модель смеси, в состав которой входит  три (в данном случае) равноправных  компонента

3)      (5)

       где  – i-я характеристика доминирующего компонента;  – параметры модели без учёта взаимодействия компонентов;  ‑ параметры модели, учитывающие взаимодействие компонентов;  – помеха, обусловленная неидеальностью модели и ошибкой эксперимента.

Это модель смеси, в которой один компонент является основным, а остальные добавляются в смесь последовательно, но на свойства смеси не влияют.

Для определения коэффициентов модели смеси могут быть использованы разные методы, рассмотрим один из них – метод наименьших квадратов, суть которого продемонстрируем на модели трехкомопонентной смеси с равноправными компонентами.

Составляется несколько смесей с различными массовыми долями  (n ‑ номер комбинации смеси) и при каждой n-й комбинации смеси измеряется значения  физической величины Y, вычисляется значение  при известных параметрах  .

Применяя, например, линейное приближение зависимости поправки от массовых долей (), получим систему определяющую искомые коэффициенты:

При моделировании смеси немаловажно определить и оптимальное соотношение исходных компонентов смеси, так как качественные характеристики компонентов смеси являются параметрами  управляемыми [1].

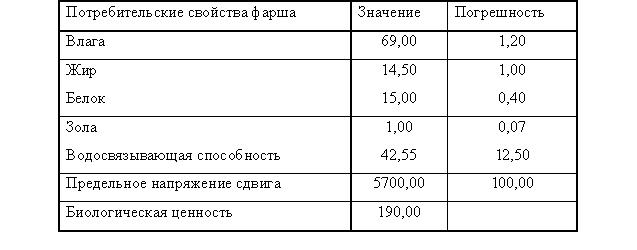
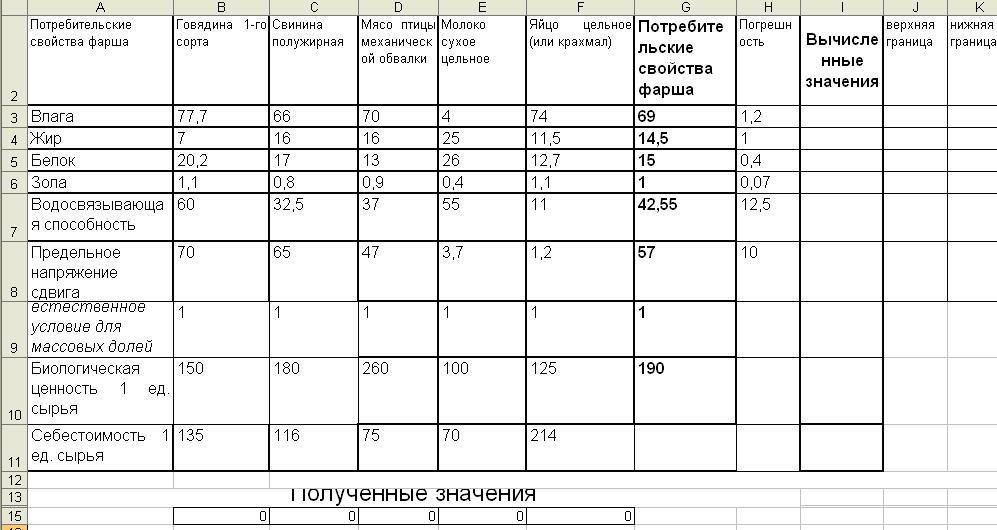
Рассмотрим пример моделирования мясного фарша. Ранее данная смесь определялась 4 компонентами, запланировано введение в состав смеси 5-го компонента (мясо птицы).  Моделируемая смесь по потребительским свойствам должна соответствовать стандартам. Опорные требования (стандарты) мясного фарша определены  в таблице 1;  компоненты  и их потребительские свойства – рисунок 1:

Таблица 1

Стандартные требования к качественным свойствам мясного фарша [1],[2]

1. Математическая модель смеси:

Введем обозначения:

x₁  - оптимальное содержание 1-го компонента

x₂ ‑ оптимальное содержание 2-го компонента

x₃ ‑ оптимальное содержание вводимого (3-го) компонента

x₄ ‑ оптимальное содержание 4-го компонента

x₅  ‑ оптимальное содержание 5-го компонента

Целевая  функция (себестоимость): 

Система ограничений:

2. Результаты моделирования (пакет Поиск решения в Microsoft Excel)

Рисунок 1 – Шаблон решения  задачи

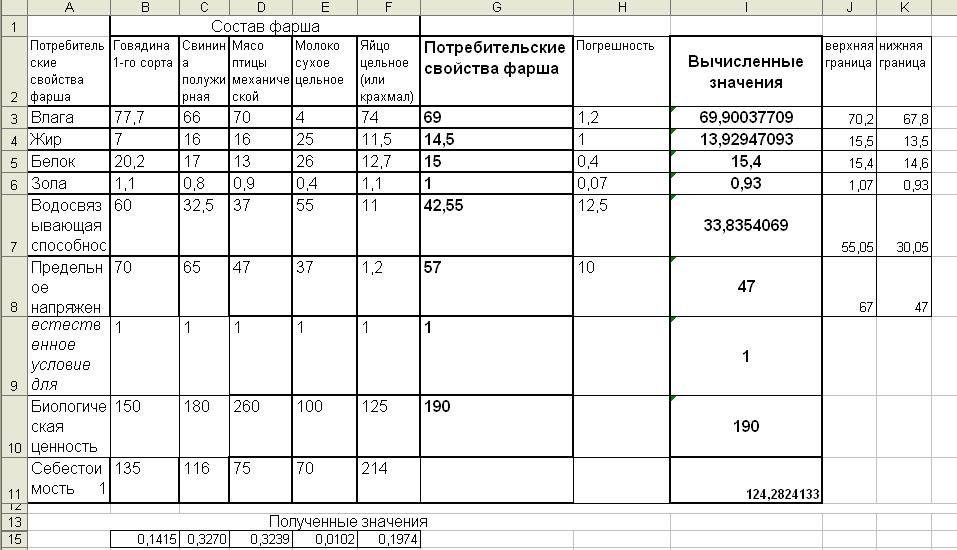
Рисунок 2 – Окно результатов

Таким образом, получено оптимальное соотношение компонентов технологической смеси (полученного фарша), рассчитано минимальное значение его себестоимости.

Моделирование количественного соотношения компонентов смеси является важным процессом, так как качественные характеристики конечного продукта являются е параметрами  неуправляемыми [3].

1. Краснов А.Е., Красуля О.Н., Большаков О.В., Шлёнская Т.В. Информационные технологии пищевых производств в условиях неопределённости.  М.: ВНИИМП, 2001. 496 с.
2. Зеленина Л.И. Разработка и применение численных методов для комплексных программ актуальных задач пищевой промышленности.: Диссертация на соискание ученой степени кандидата технических наук. Москва, 2006. 167с.
3. Сысоев В.В., Матвеев М.Г., Бугаев Ю.В. Математическое моделирование детерминированных технологических систем. Учебное пособие, – Воронеж: 2004.  77 с.
4. Комарова Н.В., Рубчинский А.А. Моделирование и оптимизация технологических систем. Учебное пособие – М.: ВЗПИ, 2000.  175 с.

Все статьи автора «Зеленина Лариса Ивановна»