Среднегодовая температура приземного слоя атмосферы являются одной из важнейших характеристик любого ландшафта, во многом определяющей особенности и состояние образующих его биоценозов, почв и водных объектов. Поэтому совершенствование методик прогнозирования характеристик ее изменчивости является актуальной проблемой не только климатологии, но также физической географии и геофизики ландшафтов.
Учитывая существенную инерционность динамики большинства компонентов ландшафтов, значительный практический интерес представляет прогнозирование такой характеристики изменчивости рассматриваемой характеристики, как ее климатическая норма. Упомянутая характеристика рассчитывается как среднее арифметическое среднегодовых температур приземного слоя атмосферы в пункте наблюдения, относящихся к некоторому промежутку времени продолжительностью 30 лет. Поэтому она является характеристикой местного климата этого пункта на подобном промежутке времени.
Как и любая другая характеристика местного климата, климатическая норма среднегодовой температуры воздуха над той или иной местностью обусловлена действием глобальных, крупномасштабных, и региональных факторов.
К числу наиболее существенных глобальных факторов изучаемого процесса относятся изменения климатических норм среднегодовых значений средней концентрации в воздухе диоксида углерода, а также средней глобальной температуры подстилающей поверхности нашей планеты, фактически определяющих парниковый эффект в земной атмосфере [1].
Одним из важнейших крупномасштабных факторов изменчивости температурного режима той или иной местности является состояние атмосферной циркуляции, которое в любом регионе Северного полушария, расположенном в зоне влияния Атлантики, определяется значениями циркуляционных индексов: – индекса Североатлантического колебания (далее САК), а также Атлантической мультидекадной моды (далее АМО).
Индекс САК определяется значением разности атмосферных давлений в Азорском максимуме и Исландском минимуме. Он влияет на отклонения от зонального направления траекторий движения на Европу воздушных масс и циклонов, сформировавшихся над Атлантикой [2,3]. При его положительных значениях смещения подобных траекторий к северу увеличивается, а при отрицательных – уменьшается, что способно существенно влиять на теплосодержание воздуха господствующего над той или иной местностью.
Индекс АМО характеризует среднюю поверхностную температуру акватории Атлантического океана, расположенной к северу от экватора. Увеличение его значений приводит к увеличению температуры и абсолютной влажности воздуха, движущегося с Атлантики на Европу, и тем самым способствует потеплению климата в любом ее регионе [4].
К региональным факторам изменений климатических норм среднегодовых температур в некотором пункте наблюдения относятся вариации характеристик подстилающей поверхности, влияющих на тепловой баланс изучаемого сегмента приземного слоя атмосферы. Их совместное действие приводит к тому, что между изменениями этих характеристик в пунктах, относящихся к одной и той же ландшафтной области, существует значимая статистическая связь [5].
Наряду с подобными факторами, на рассматриваемый процесс действуют также многие другие ненаблюдаемые факторы, вследствие чего его целесообразно рассматривать как многофакторный случайный процесс.
Одним из наиболее универсальных методов моделирования подобных процессов является метод множественной регрессии. Упомянутый метод применим и для их прогнозирования, в случае, если имеются достаточные основания полагать, что характеристики статистических связей изучаемого процесса и его факторов с течением времени изменяются несущественно. Последнее позволяет рассчитать по предысториям данного процесса и его факторов коэффициенты соответствующего уравнения множественной регрессии, а также применять это уравнение как прогностическое [6].
В задачах прогнозирования изменений климатических норм среднегодовых температур приземного слоя атмосферы, условия, позволяющие применить упомянутый метод, выполняются лишь приближенно, а построенные с его помощью прогнозы всегда характеризуются некоторой ошибкой, среднеквадратическое отклонение которой, как правило, увеличивается по мере увеличения их упреждения.
Поэтому возможность применения данного метода для прогнозирования рассматриваемого процесса в том или ином районе мира существенно зависит от его географического положения, а также наличия вблизи от него (в той же ландшафтной области) пунктов, в которых ведутся аналогичные наблюдения.
Оценка указанных возможностей наиболее актуальна для районов, обладающих высоким рекреационным и сельскохозяйственным потенциалом и традиционно являющихся курортами. Одним из таких районов является Южный берег Крыма, имеющий международное значение, район выращивания уникальных сортов винограда, садовых и эфиромасличных культур, важнейший район виноделия. Эстетическая привлекательность ландшафтов ЮБК обусловлена расположением на границе контрастных сред суша – море. Известняковые массивы в сочетании с субсредиземноморской растительностью, обладают высокой привлекательностью для туристической и рекреационной деятельности. Лесные массивы ЮБК обладают высоким средообразующим потенциалом. Социально-экономические функции ландшафтного уровня Южного берега Крыма трудно переоценить, так как они имеют не только общегосударственное, но и международное значение [7].
На Южном берегу Крыма за изменениями температур приземного слоя атмосферы режимные наблюдения ежесуточно и практически непрерывно, с 80-х годов XIX века, осуществляются в пунктах Ялта, Алушта, Феодосия. В непосредственной близости от Ялты аналогичные наблюдения ведутся на метеостанции Ай-Петри, расположенной на яйле. С конца XIX века до 2008 года данные были получены с сайта European Climate Assessment & Dataset [8], а с 2009 по 2014 годы – из архивов российского сайта rp5.ru [9]. Это позволило сформировать весьма представительные временные ряды изучаемых характеристик.
На соответствующих Интернет-сайтах [10-11] представлены временные ряды изменений упомянутых глобальных и крупномасштабных индексов рассматриваемого процесса. Тем не менее, возможности применения метода множественной регрессии для прогнозирования климатических норм среднегодовых температур приземного слоя атмосферы над пунктами Южного берега Крыма ныне изучены недостаточно. Это не позволяет использовать данный метод для построения соответствующих прогнозов, необходимых для эффективного социально-экономического развития данного региона.
Учитывая изложенное, в качестве объекта исследования в данной работе выбраны изменения среднегодовых температур приземного слоя атмосферы в пунктах Южного берега Крыма.
Предметом исследования является эффективность прогнозирования изменений климатических норм среднегодовых температур приземного слоя атмосферы на Южном берегу Крыма, с использованием метода множественной регрессии.
Целью работы является разработка методики прогнозирования рассматриваемых характеристик, а также оценка адекватности подобных прогнозов.
Фактический материал и методика исследования.
Для достижения указанной цели в качестве фактического материала использованы временные ряды среднегодовых значений: средней концентрации в земной атмосфере диоксида углерода [10], индекса глобальной температуры подстилающей поверхности нашей планеты, индекса САК, индекса АМО [11], температур приземного слоя атмосферы в пунктах Ялта, Алушта, Феодосия, Ай-Петри, Херсонесский маяк и Севастополь [7, 8].
Как известно, эффективность моделирования с помощью метода множественной регрессии многофакторных временных рядов, обладающих свойствами близкими к изучаемым, тем выше, чем больше размерность уравнения регрессии (чем больше факторов в нем учитывается). Статистической устойчивостью коэффициенты этого уравнения обладают, если длина фрагмента каждого временного ряда, учитываемого при их расчете превышает размерность уравнения регрессии не менее чем в 2 раза [6].
Как прогностическое уравнение для каждого изучаемого процесса рассматривалось линейное уравнение регрессии максимально возможной размерности. Учитывая имеющийся фактический материал, в качестве такого уравнения выбрано линейное уравнение, связывающее изучаемый процесс с 38 факторами. При вычислении коэффициентов для каждого фактора использованы фрагменты временных рядов, содержащие 78 членов.
При построении прогнозов климатических норм среднегодовых температур в г. Ялта и г. Алушта итеративно решалась система уравнений, которая имеет вид:
Тяк+1= с0+с1* Тяк-13+…+с13*Тяк + с14*GTк+1+…+с26* GTк-12+с27*Dк+1+c28* Dк+
c29*Aк+1+ c30*Aк+ c31*Aк-1+ c32*Nк+1+ c33*Nк+ c34*Тaк+…+ c39*Тaк-6 (1)
Так+1= с0+с1* Тяк-12+…+с13*Тяк+1 + с14*GTк+1+…+с26* GTк-12+с27*Dк+1+c28* Dк+
c29*Aк+1+ c30*Aк+ c31*Aк-1+ c32*Nк+1+ c33*Nк+ c34*Тaк+…+ c39*Тaк-6 (2)
Здесь Тяк+1 – прогноз климатической нормы среднегодовой температуры в г. Ялта, основанный на учете предыдущих -к членов соответствующего временного ряда, который опережает последний из этих членов на 1 год;
Тяк – последний из учитываемых членов временного ряда, климатической нормы среднегодовой температуры в г. Ялта, используемый для построения прогноза;
Dк+1 – прогноз с упреждением 1 год климатической нормы среднегодового значения средней концентрации в атмосфере СО2, разработанный в [10 ];
GTк+1 – прогноз с упреждением 1 год климатической нормы среднегодового значения индекса GMSST, рассчитанный с помощью модели авторегрессии скользящего среднего [12 ];
Aк+1 – прогноз с упреждением 1 год климатической нормы среднегодового значения индекса АMО, рассчитанный с помощью модели авторегрессии скользящего среднего [12];
Nк+1 – прогноз с упреждением 1 год климатической нормы среднегодового значения индекса САК, рассчитанный с помощью модели авторегрессии скользящего среднего [12 ];
Тaк – последний из учитываемых членов временного ряда, климатической нормы среднегодовой температуры в г. Алушта, используемый для построения прогноза.
Как видно из уравнений (1, 2) первое обеспечивает построение прогноза Тя, с упреждением 1 год (последний член ряда Тя, учитываемый при построении прогноза, соответствует периоду 1984–2013 гг., следовательно, прогноз делается на период 1985-2014 гг.). Значение этого прогноза используется в качестве аргумента в уравнении (2), которое обеспечивает построение прогноза Та с упреждением 1 год (на период 1985–2014г.).
Процедура начинается с задания к=13. Из уравнения (1) находим Тя14, которое подставляем в (2), что позволяет найти Та14. Далее увеличиваем к на 1, если к<20, то повторно решаем (1) уравнение, полагая в нем Тяк= Тя14, Тaк= Та14.(это позволяет получить прогноз следующий год Тя15), а также уравнение (2) (что дает Та15) . Подобный расчет продолжается до тех пор, пока к не достигнет 20. На этом процедура останавливается. В результате ее осуществления формируются прогнозы с упреждением 1–6 лет временных рядов Тя и Та.
Очевидно, что оптимальным по критерию минимум среднеквадратической ошибки является лишь прогноз Тя с упреждением 1 год (для вычисления которого используется только достоверная информация – фактический материал). Для построения всех остальных прогнозов используются те или иные сочетания фактического материала и прогнозов, рассчитанных на предыдущих этапах данной процедуры. Вследствие этого ошибка прогноза по мере увеличения упреждения накапливается и увеличивается. Учитывая последнее, прогнозы с упреждением более 6 лет нами не строились (хотя каких либо принципиальных ограничений для их вычисления нет).
Чем больше расстояние между пунктами одной и той же ландшафтной области (ЮБК), тем слабее статистическая связь между изменениями в них климатических норм среднегодовых температур приземного слоя атмосферы.
Для этого для пункта Ялта расчет прогнозов был повторен, с использованием в качестве аргументов Та, соответствующих данных, полученных на метеостанции Ай-Петри. Для пункта Алушта такой же повторный расчет проведен с использованием данных, полученных на метеостанции Феодосия.
Об адекватности разработанных прогнозов может свидетельствовать качественное соответствие теоретическим представлениям, а также устойчивость к изменению состава аргументов (замене пункта, данные по которому использованы как региональные факторы).
Результаты и их анализ
С помощью описанной методики построены прогнозы изменения климатических норм среднегодовых температур для пунктов: Ялта, Алушта, Ай-Петри, Феодосия, Севастополь и Херсонесский маяк.
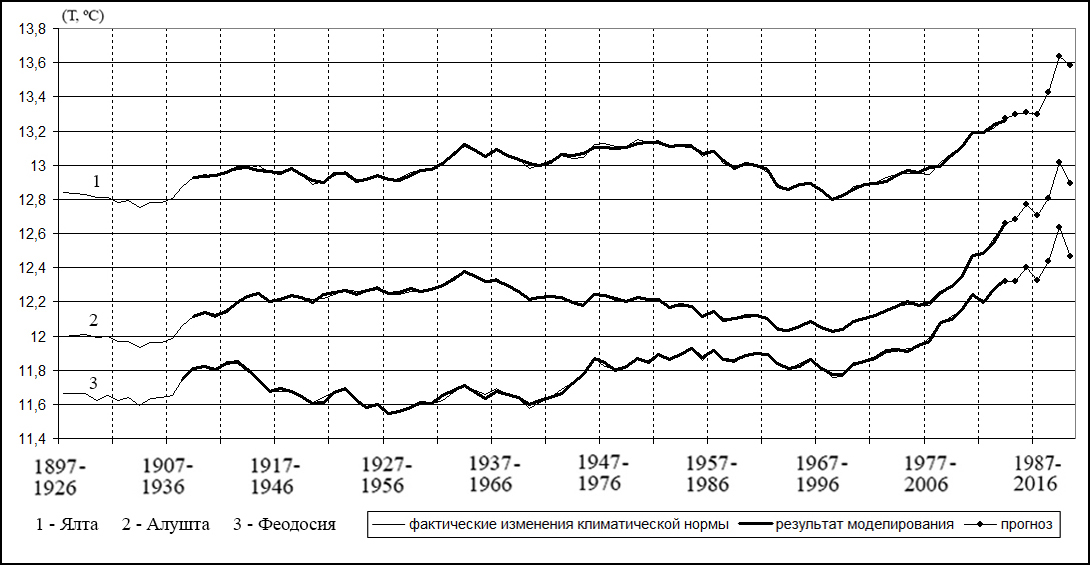
На рисунке 1 представлены фактические изменения климатических норм среднегодовых температур по Ялте (с учетом данных по Ай-Петри и Алуште), по Алуште (с учетом данных по Феодосии и Ялте) и по Феодосии (с учетом данных по Алуште), а также результаты их моделирования и прогнозирования.
Рисунок 1. Фактические изменения климатических норм среднегодовых температур, результаты моделирования и прогнозирования по Ялте (с учетом данных по Ай-Петри и Алуште), по Алуште (с учетом данных по Феодосии и Ялте) и по Феодосии (с учетом данных по Алуште).
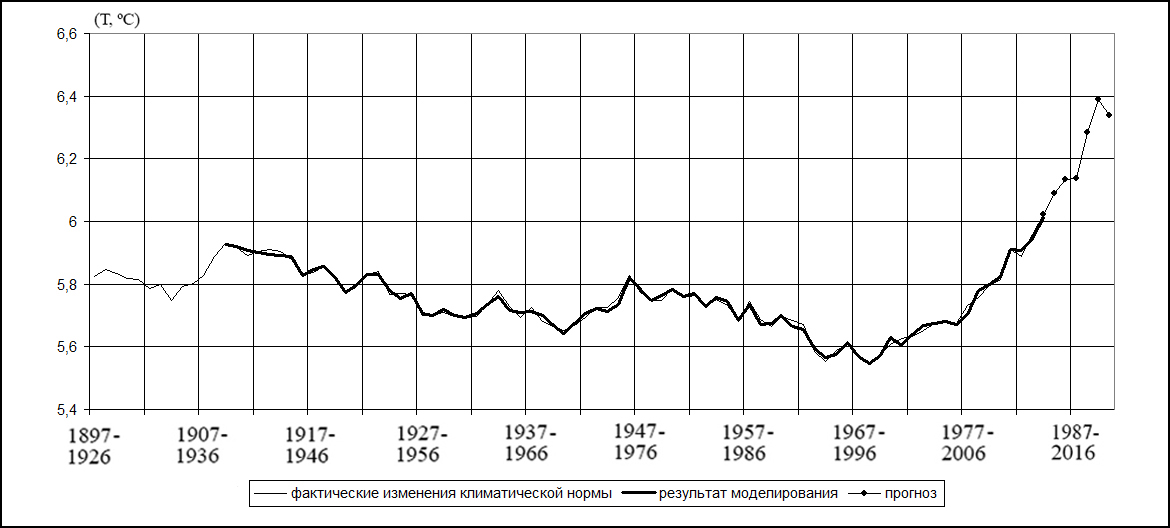
На рисунке 2 изображены фактические изменения климатических норм среднегодовых температур по Ай-Петри (с учетом данных по Ялте), а также результаты их моделирования и прогнозирования.
Рисунок 2. Фактические изменения климатических норм среднегодовых температур, результаты их моделирования и прогнозирования по Ай-Петри (с учетом данных по Ялте).
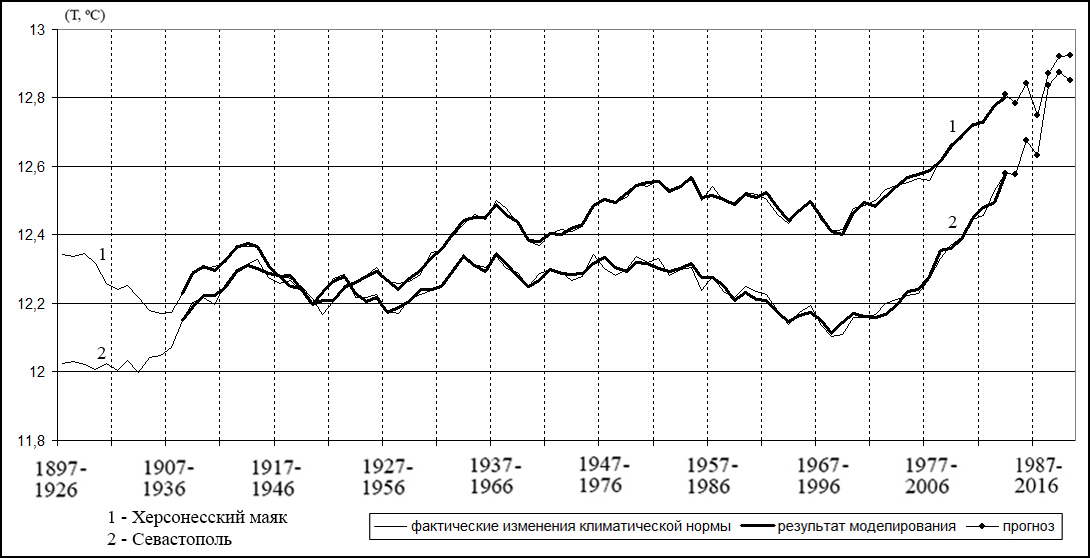
На рисунке 3 отображены фактические изменения климатических норм среднегодовых температур по Херсонесскому маяку (с учетом данных по Севастополю) и по Севастополю (с учетом данных по Херсонесскому маяку), а также результаты их моделирования и прогнозирования.
Рисунок 3. Фактические изменения климатических норм среднегодовых температур, результаты моделирования и прогнозирования по Херсонесскому маяку (с учетом данных по Севастополю) и по Севастополю (с учетом данных по Херсонесскому маяку).
Как видно из рисунков 1 – 3, с 2014 по 2019 годы для всех рассматриваемых пунктов прогнозируется повышение среднегодовой температуры. Так, для Ялты – на 0,4 ºС, для Алушты – на 0,3 ºС, для Феодосии – на 0,3 ºС, для Ай-Петри – на 0,4 ºС, для Херсонесского маяка – на 0,1 ºС и для Севастополя – на 0,3 ºС.
Выводы
Предложенная методика позволяет строить прогнозы изменений климатических норм среднегодовых температур для Южного берега Крыма, которые качественно соответствуют представлениям о вероятных последствиях происходящего увеличения содержания в атмосфере диоксида углерода и потепления глобального климата.
Прогнозы изучаемых процессов для всех рассматриваемых пунктов Южного берега Крыма, разработанные с учетом различных региональных факторов, качественно совпадают между собой, что свидетельствует об их адекватности.
Библиографический список
- Climate Change 2007 – Impacts, adaptation and vulnerability. Contribution of Working Group II to Assesment Report Four of the Intergovernmental Panes of Climate Change (IPCC). Cambridge Unsversity Press. – Cambridge. – UK, 2007. – 973p.
- Walker G.T. World weather V / G.T.Walker, E.W.Bliss // Meteorology. Royal Meteorology Society. – 1932. – V. 4. – No 36. – P.53 – 84.
- Клімат України / Під ред. Ліпінського В.М., Дячука В.А., Бабічєнко В.М. – К.: Видавництво Раєвського, 2003. – 343 с.
- Knight J., Allan R., Folland C. and ather. The Atlantic Multidecadal Oscilation: A Signature of Thermohaline Circulation Cycles in Obsered Climate//CRCES Workshop on Decadal Climate Variability. – 19. October 2005.
- Будыко М.И. О связи альбедо подстилающей поверхности с изменениями климата / М.И.Будыко, И.М.Байкова, Н.А.Ефимова, Л.А.Строкина // Метеорология и гидрология. – 1998. – № 6. – С. 5.
- Кобзарь А. И. Прикладная математическая статистика. – М.: Физматлит, 2006. – 816 с.
- Позаченюк Е.А. Современные ландшафты Крыма и сопредельных территорий: Монография // Научный редактор Е. А. Позаченюк. – Симферополь: Бизнес-Информ, 2009. – 672 с.
- European Climate Assessment & Dataset. [Электронный ресурс]. – Режим доступа: http://eca.knmi.nl/
- Погода в 243 странах мира. [Электронный ресурс]. – Режим доступа: http://www.rp5.ru
- Goddard Space Flight Center. [Электронный ресурс]. – Режим доступа: http://data.giss.nasa.gov/modelforce/strataer/
- National Climatic Data Center. [Электронный ресурс]. – Режим доступа: http://www.ncdc.noaa.gov
- Бокс Дж. Анализ временных рядов. Прогноз и управление / Дж. Бокс, Г. Дженкинс; пер. с англ. Л.Л. Левшина; под ред. Писаренко В.Ф. – М.: Мир, 1974. – 197 с.