Систематические коды могут использоваться для контроля сложения, вычитания или умножения.
Сумматор, который использует систематический код для контроля результатов, показан на рисунке 1. Из-за систематического характера кода, можно разделить сумматор на две части. Операнды Х и Y поданы в арифметическую единицу.
Единица, которая обрабатывает контрольные цифры С(Х) и C(Y) будет называться процессором кода. Процессор кода выполняет произвольную операцию над цифрами контроля. Пусть эта операция будет обозначена #. Выход процессора кода С(Х) # C(Y) должен быть С(Х+Y). Значение С(Х+Y) подается в компаратор для сравнения с С’(Х+Y), где С’(Х+Y) представляет цифры контроля созданные из выхода арифметической единицы. Теперь будет показано, что систематические коды С(Х) и C(Y) должны быть остаточными кодами, и что операция обозначенная # это остаточное сложение, если арифметическая операция выполненная с Х и Y это сложение.
Эти пункты будут иллюстрированы тем, что коды контроля должны иметь периодичность т, такую чтобы код сам по себе имел характерные атрибуты mod-m остаточного кода.
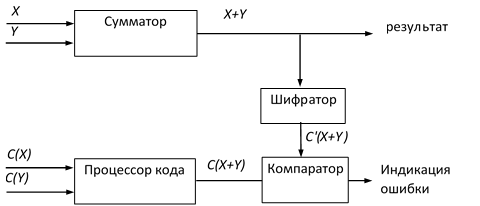
Рисунок 1 – Контроль арифметических операций
В обсуждаемых ошибках в позиционной системе счисления легко определить их множественность для кода передачи. Множественность ошибок, т.е. единичных, двоичных, и т. д., определяется числом неправильных цифр в полученном послании. Для последовательной передачи слов данных, множественность ошибок может вести к продолжительности времени случая помехи.
Соответствующий вычислительному коду, определение множественности ошибок является более сложным и соотношение ошибок с физическим повреждением определить не легко. Для вычислительных кодов, множественность ошибок определяется следующим образом.
Пусть X и Y будут операндами в позиционной системе счислением S. Обозначим полученный результат арифметической операции Z¢и аналитически правильный результат Z . Тогда ошибка, Z¢ – Z выражена одним или более расширением вида.
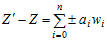 (1)
(1)
где цифры в системе счисление Sобозначены аi и соответствующие веса представлены wi.
В системе счисления S, Z¢ – Z может быть выражено несколькими уравнениями вида уравнение (1).Множественность ошибок определяется как число ненулевых элементов в таком выражении для Z¢- Z который сам по себе имеет наименьшее число ненулевых элементов.
Пример 1: Множественность ошибок в двоичном сложении.
Рассмотрим два числа и их сумму в двоичной системе:
01011
00101
10000
Если из-за ошибки, не образовался перенос в наименее значимой позиции, получится следующий результат: 01110. Неправильный ответ отличается от правильного в четырех цифровых позициях. В системе кода переноса, будет рассмотрена учетверенная ошибка. Однако, следующее определение данного для множественности ошибок в вычислительном коде:
Z¢ – Z = 01110 –10000 = -2
Это может быть выражено как -1´2: или -1´ 22 + 1´ 21 , или -1´ 23+ 1´ 22+1´21, и т. д. Понятно, что первое выражение имеет наименьшее число ненулевых элементов, а именно, один. Следовательно, это единственная ошибка, а не учетверенная.
Если результат сложение был бы 11110, это была бы двойная ошибка, т.к.
Z’ – Z = 11110 – 10000 = +1´24 – 1´21.
Обнаружение единичной ошибки систематическими кодами
Пусть S будет произвольной позиционной системой счисления, с Х и Y как второе слагаемое и первое слагаемое, соответственно. Предположим, что единичная ошибка возникла в операции сложения, и что итоговая сумма это Z¢. Если Z правильная сумма, то по определению единичная ошибка Z¢ – Z выражается как
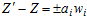
где аi и wi это цифры и позиции в системе счисления S.
Подберем значение т так чтобы 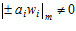 для любых аi и wi. Тогда
для любых аi и wi. Тогда
Z=Х+Y
ясно│Z│т=│Х+Y│т= ││Х│т+│Y│т│т
│Z’│т=│Х+Y±aiwi│т
Если 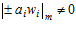 для любых аi и wi в системе S, единичную ошибку можно обнаружить, используя следующий алгоритм:
для любых аi и wi в системе S, единичную ошибку можно обнаружить, используя следующий алгоритм:
-
Вычислим (или сделаем доступным) │Х│т и │Y│т.
-
Вычислим ││Х│т+│Y│т│ти │Z’│т.
-
Вычислим ││Х│т+│Y│т│т с │Z’│т.
Если ││Х│т+│Y│т│т ≠ │Z’│т существует ошибка.
Этот метод контроля ошибок известен как обобщение хорошо известной процедуры “выбор из девяти”. Отметьте ограничительный характер результата. Если ││Х│т+│Y│т│т не равен │Z’│т это еще не значит, что только единичная ошибка существует, т.к. множественную ошибку могут привести к такому же результату. Более того, если параметры равны, это тоже не исключает возможности, что возникла ошибка множественности больше 1.
Система, как описано, предполагает, что ошибка может возникнуть только в арифметической единице, которая обрабатывает операнды, выраженные в системе счисления S. Сбой в процессоре кода (в этом случае остаточный сумматор) или в кодирующем устройстве, который создает цифры контроля из итоговой суммы, выйдет результатом в индикации ложной ошибки. Даже не смотря на то, что арифметическая единица может быть без сбоев. Это, конечно, знакомая проблема, облегченная большей частью тем фактом, что сложность контролируемой части системы обычно меньше чем сложность самой арифметической единицы, так что присутствуют соответствующие возможности сбоев. Может применен хорошо известный подход дублирования критических частей системы для получения желаемых возможностей сбоя.
Пример метода для обнаружения единичных ошибок следующий.
Пример 2: Обнаружение единичной ошибки в двоичном сложении.
1101 ↔ 13
1010 ↔+10
10111 ↔ 23
Предположим, что существует ошибка и полученный результат 11111↔ 31.
В этом случае аi может быть 1 или 0, а wi =2i. Так как 2i для любых i является соответственно простым для 3, требование, что 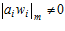 легко осуществляется при т=3.
легко осуществляется при т=3.
Проверяя единичные ошибки, получаем
│13│3=1 │10│3=1 │31│3=1
и ││13│3+│10│3│3 = 2 ≠ │31│3
Результат показывает, что ошибка существует.
Можно увидеть, что модуль S можно тоже использовать для обнаружения единичной ошибки в двоично-десятичной системе.
Исправление ошибок систематическими кодами
В вычислительных кодах, как правило, в кодах передачи возможна скорее коррекция, чем распознавание ошибок, если используются дополнительные цифры. Обычно, в кодах передачи, код коррекции можно обработать так, чтобы особые цифры в ошибке были специально обозначены. Подобная ситуация существует в вычислительных кодах, кроме случаев скорее с величиной ошибки, чем с обозначением местоположения.
В n – цифровом двоичном ответе может возникнуть 2n возможных единичных ошибок т.к., как отмечалось ранее, ошибка в каждой позиции может быть либо положительной. Либо отрицательной. Остаточная система, используемая для представления контроля цифр должна иметь значение т по крайней мере такое же большое как 2n+1, если все возможные единичные ошибки готовы к расположению. (Дополнительный режим требуется для обозначения отсутствия ошибок).
Необходимые и значимые требования для коррекции единичной ошибки в позиционной системе счисления:
1. m 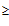 N + 1, где N это число возможных единичных ошибок.
N + 1, где N это число возможных единичных ошибок.
2. Остаток, по модулю m, любых двух различных единичных ошибок должен различаться.
Эти требования принимают следующий вид в случае двоичной системы счисления:
1. Для n двоичных цифр, возникает 2n возможных ошибок. Отсюда, m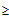 2n + 1 (т.е., 2n=N).
2n + 1 (т.е., 2n=N).
2. Для двоичной системы, для любых i и j, где 0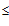 i, j < n , i ¹ j,
i, j < n , i ¹ j, 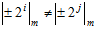 .
.
Процесс коррекции ошибок будет показан в следующем примере.
Пример 3: Коррекции ошибок в 5- бит двоичном сумматоре.
В случае 5-битной двоичной системе, m = 11 удовлетворяет двум условиям описанным ранее. Это значение для m дает код максимальной эффективности, т.к. 2n + 1=m . Таблица 1 показывает используемый код цифры контроля.
Таблица 1 – Код коррекции для 5-бит системы.
| Цифра контроля |
ошибка |
| 0 |
0 |
| 1 |
+20 |
| 2 |
+21 |
| 3 |
-23 |
| 4 |
+22 |
| 5 |
+24 |
| 6 |
-26 |
| 7 |
-27 |
| 8 |
+28 |
| 9 |
-21 |
| 10 |
-20 |
Операция, для контроля следующая сложим
01101 ↔ 13
01001 ↔9
10110 ↔ 22
Предположим, что есть ошибка, и что полученный результат 00110  6. Тогда,
6. Тогда, 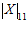 =
= 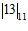 =2 ,
=2 , 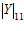 =
= 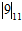 = 9, и
= 9, и 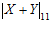 =
= 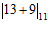
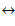 0 Z’ =
0 Z’ = 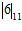 = 6, следовательно,
= 6, следовательно, 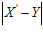 11= 6 .
11= 6 .
Таблица показывает, что ошибка –24, т.е. что 24 должно быть прибавлено к 00110, неправильному результату, для получения 10110, правильного результата.
Коррекция ошибок с многомодульными кодами
Между коррекцией ошибок описанной в предыдущем обсуждении, и показанной в примере 3, поднимает некоторые практические трудности. Первое, требование для m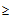 2n+1 обычно выходит результатом в большом значении для модуля m, т.к. число бит n, обычно больше 20. Второе, есть повторное требование для операции свободной от ошибок остаточного процессора используемого в контрольном канале.
2n+1 обычно выходит результатом в большом значении для модуля m, т.к. число бит n, обычно больше 20. Второе, есть повторное требование для операции свободной от ошибок остаточного процессора используемого в контрольном канале.
Требовании для операций для каналов коррекции можно встретить частично путем разработки процессора коррекции на столько простого и, следовательно, надежного на сколько возможно. Если надежность, таким образом, достигнутая не достаточная, то прямой подход будет заключаться в дублирование канала коррекции. Тогда будет возможным сравнить выводы двух процессоров коррекции в качестве контроля над этой частью процесса.
Дублирование каналов коррекции поднимает много проблем, изучая вопрос повышенной надежности путем добавление резервированного оборудования. Например, если две идентичные системы (или каналы, в этом случая) используются, и если выводы отличаются, какой из двух правильный. Более полезный метод будет заключаться в применении некоторых концентрации контроля ошибок. В особенности, выгодно использовать отдельные модули в системе коррекции, так чтобы простой контроль канала коррекции, как правило, информационный канал, может быть более экономичным, чем дублированные системы контроля.
Библиографический список
- Горденко Д.В., Резеньков Д.Н., Яйлаханов С.В. Высоконадежные комплексы и средства связи на нейросетевых элементах. Москва, 2010.
- Калмыков И.А., Резеньков Д.Н., Горденко Д.В., Саркисов А.Б. Методы и алгоритмы реконфигурации непозиционных вычислительных структур для обеспечения отказоустойчивости спецпроцессоров. Монография. / – Ставрополь: издательско- информационный центр «Фабула». – 2014.
- Горденко Д.В., Токарева Г.В. Нейронная сеть для преобразования чисел, представленных в позиционном коде в систему остаточных классов // В сборнике: Информационные системы и технологии как фактор развития экономики региона 2013.
- Горденко Д.В., Горденко Н.В. Нейронная реализация локализации ошибок в модулярном коде // Исследования в области естественных наук. 2013. № 7 (19).
- Горденко Д.В. Принципы построения модулярных отказоустойчивых специализированных процессоров для обработки информации // Исследования в области естественных наук. 2013. № 8 (20).
- Горденко Д.В. Перспективное развитие вычислительной техники на основе непозиционного нейрокомпьютера // Исследования в области естественных наук. 2013. № 12 (24).
- Горденко Д.В., Горденко Н.В. Нейронная сеть Хэмминга для преобразования модулярного кода в позиционный // Исследования в области естественных наук. 2013. № 11 (23).
- Горденко Д.В., Токарева Г.В. Принципы построения модулярных отказоустойчивых специализированных процессоров для обработки экономической информации // В сборнике: Актуальные проблемы развития агробизнеса в условиях модернизации экономики 2012.
- Горденко Д.В., Пономаренко М.В. Применение AN-кодов для коррекции ошибок в модулярных нейрокомпьютерах в области экономики // В сборнике: Актуальные проблемы развития агробизнеса в условиях модернизации экономики 2012.
- Горденко Д.В., Резеньков Д.Н., Сапронов С.В. Нормированный след полинома в процедурах поиска и локализации ошибок в модулярных кодах // Вестник СевКавГТИ. 2010. № 10.
- Горденко Д.В., Горденко Н.В. Локализация ошибок в устройствах цифровой обработки сигналов на основе алгебры полиномов // Вестник СевКавГТИ. 2009. № 9.
- Горденко Д.В., Горденко Н.В., Павленко Н.А., Павлюк Д.Н., Ткачук Р.В. Коррекция ошибок в системе остаточных классов с минимальной временной сложностью на основе метода расширения оснований // Известия высших учебных заведений. Северо-Кавказский регион. Серия: Технические науки. 2007. № 4.
- Ткачук Р.В., Горденко Д.В., Павлюк Д.Н., Малофей А.О. Активная безопасность на основе криптографического мультинейропроцессора обработки данных // Известия высших учебных заведений. Северо-Кавказский регион. Серия: Технические науки. 2007. № 4.
- Червяков Н.И., Горденко Д.В. Нейронная сеть для округления и масштабирования чисел, представленных в системе остаточных классов // патент на изобретение RUS 2271570 26.05.2003.
- Червяков Н.И., Горденко Д.В., Сивоплясов Д.В., Ткачук Р.В. Модулярный сопроцессор для обработки биометрической информации // Известия Южного федерального университета. Технические науки. 2003. Т. 33. № 4.


