Уравнения над числовыми структурами были обобщены до уравнений над свободными полугруппами и группами. В 1962 году Мальцев А.И. в своей статье [1] рассматривал уравнения вида  в свободной группе. В 1977 году Маканин Г.С. в своей статье «Проблема разрешимости уравнений в свободной полугруппе»[2] впервые сумел построить алгоритм, распознающий разрешимость произвольных уравнений в свободной полугруппе. Позднее, в 1982 году Маканин Г.С. в соавторстве с Разборовым А.А.  выпустил статью «Уравнения в свободной группе»[3], в которой он рассматривал  решения уравнения уже над свободной группой. 
В 1984 году Разборов А.А. и Маканин Г.С. в своей совместной статье «Системы уравнений в свободной группе»[4] дали описание общего решения данного показателя периодичности для произвольной системы уравнений в свободной группе. На основании полученного результата они построили алгоритм, вычисляющий ранг бескоэффициентных систем уравнений.
По аналогии с вышеприведенными работами, в 1992 году в работе [5]  уравнения в свободной алгебре Ли  рассмотрел Шантаренко В.Г.  В его работе изучаются вопросы, связанные с разрешимостью уравнений в свободной алгебре Ли и проблемой аппроксимируемости алгебр Ли свободными алгебрами Ли. В частности, вычислены ранги некоторых бескоэффициентных уравнений в свободной алгебре Ли, построена бесконечная счетная серия решений для уравнений ранга 2. В.Н. Ремесленников и R.Stohr в 2007 году в статье [6] получили еще 2 бесконечные серии решений этого уравнения.
Техника вычислений, использованная в данной работе близка технике работы [7] .
Для дальнейшего изложения введем предварительные понятия, следуя работе Ширшова А.И. [8]. 
Пусть   R =  — некоторое множество символов, где  пробегает ка­кое-то непустое множество индексов. Из элементов множества R могут быть образованы неассоциативные слова всевозможной длины. [8, 471]
Определение. Будем говорить, что два неассоциативных слова и, v имеют одинаковый состав относительно R, если каждый элемент  входит в слова и и v одинаковое число раз.
В частности, для слов, имеющих одинаковый состав относительно R, если каждый элемент  входит в эти слова ровно по одному разу, то будем говорить, что они линейны по каждому входящему в них символу.
Определение. Длиной слова называется количество символов, входящих в данное слово. 
Ясно, что слова, имеющие одинаковый состав относительно R, имеют одну и ту же длину.
Пусть U— свободная лиева алгебра над некоторым полем Р с тем же множеством R в качестве множества свободных образующих. Элементами ал­гебры U являются линейные комбинации неассоциативных слов, образован­ных из элементов множества R, с коэффициентами из поля Р. Равными эле­ментами считаются при этом элементы, переводящиеся один в другой при по­мощи конечного числа преобразований, выполняемых или на основании законов дистрибутивности, или на основании тождественных соотношений
x² = 0,              (1)

(ху) z + (yz) х + (zx) у = 0,           (2)
или же являющихся тождественными преобразованиями в аддитивной группе. 
Пусть L=L[a,b]- свободная алгебра Ли от двух образующих  a и b, то есть R = .
Определение. Уравнение  вида

xa=yb , где  L[a,b]                         (3)

с двумя образующими a и b  называется  уравнением ранга 2 над свободной алгеброй Ли.
Определение. Решением уравнения (3) называется упорядоченный набор  из двух элементов  для которых . 
Если решение является линейной комбинацией слов одинаковой длины, будем говорить, что оно однородно. В работе рассматриваются только однородные решения данного уравнения.
Далее, под выражением «уравнение  для слов длины п» подразумеваем уравнение для которого рассматриваются только однородные решения длины п-1.
Определение. Пусть - некоторое решение уравнения (3) , назовем  это решение тривиальным, если  , в противном случае решение называется нетривиальным.
Так как уравнение (3) всегда имеет тривиальные решения, поэтому имеет смысл рассматривать лишь вопрос о существовании нетривиальных решений данного уравнения.
Определение. Неассоциативное слово, в котором скобки расставлены справа налево называется словом с правонормированной расстановкой скобок.
В дальнейшем условимся называть неассоциативные слова с правонормированной расстановкой скобок правонормированными.
Если же на слове скобки или часть скобок опущена, то будем считать, что недостающие скобки расставлены  правонормированно.
Так как любое неассоциативное слово может быть представлено в виде линейной комбинации правонормированных слов, то правонормированные слова содержат базу линейного пространства L.
Цель данной работы  заключается в рассмотрении вопроса о существовании нетривиальных решений уравнения (3) для слов длины  и указать алгоритм нахождения этих решений.
В этой статье показано, что уравнение (3) для слов длины 2,4,6 имеет нетривиальные решения, а для слов длины 3,5 нетривиальных решений нет. Также выдвинута гипотеза о том, что для слов нечетной длины нетривиальных решений нет.
Перейдем непосредственно к рассмотрению решений уравнения вида xa=yb ранга 2 в свободной алгебре Ли L[a,b] для слов длин 2,3,4,5,6.
Рассмотрим решение уравнения для слов длины 2.
Возмем  правонормированное слово длины 2 от двух образующих a и b. Здесь возможны два случая для решения нашего уравнения – это ba= – ab, то есть =b, =-a и aa=bb , т.е. = a , =b.
Пусть теперь L[a,b,с] – свободная алгебра Ли от трех порождающих. Будем рассматривать линейные комбинации правонормированных слов длины 3, линейных по каждому входящему в них символу. Итак,
(ab)c=(ac)b+a(bc)=(ac)b-(bc)a=(ac)b+(cb)a , следовательно  abc=acb+cba
Найдем все нетривиальные решения уравнения (3) для слов длины 3.  Для этого будем всевозможными способами придавать порождающим a, b, c только два значения а или b. Для случая слов длины 3 будет 2³=8 комбинаций присвоения значений а или b. Получающиеся при этом случаи удобно представить в таблице (см. таблицу 1).
Таблица 1

По результатам таблицы можно сделать вывод, что уравнение (3) для слов длины 3 нетривиальных решений не имеет. 
Пусть L[a,b,с,d] – свободная алгебра Ли от 4-х порождающих. Так же как и в случае для слов длины 3 будем рассматривать линейные комбинации правонормированных слов длины 4, линейных по каждому входящему в них символу.Получаем следующее:
(((ab)c)d)=((ad)b)c+(a(bd))c+(ab)(cd)=((ad)b)c-(bd)a)c+(a(cd))b+a(b(cd))=((ad)b)c-((bd)a)c-((cd)a)b+((cd)b)a   или    

abcd=adbc-bdac-cdab+cdba

Теперь найдем все нетривиальные решения уравнения (3) для слов длины 4.  Так же как и в случае слов длины 3  будем всевозможными способами придавать порождающим a, b, c, d только два значения а или b. Для случая  слов длины   4  будет 2⁴=16   комбинаций присвоения значений а или b.
Результаты покажем в таблице (см. таблицу 2).
Таблица 2

Выпишем полученные нетривиальные решения из таблицы.
1.        (abb)a=(aba)b    = abb, 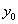 = aba – 1-е решение.
2.        (baa)b=(bab)a или (bab)a=(baa)b   = bab,  = baa – 2-е решение. (или используя тождественные соотношения (1), (2)  = abb,  = aba)
3.        (bab)a=(baa)b  = bab,  = baa – 3-е решение (или используя тождественные соотношения (1), (2)  = abb, = aba)
      4. (aba)b=(abb)a или (abb)a=(aba)b  = abb,  = aba.
На основании полученных вычислений можно сделать вывод, что  для случая слов длины 4, уравнение (3)  имеет решение = abb,  = aba.
Пусть L[a,b,с,d,e] – свободная алгебра Ли от 5-ти порождающих. Будем действовать так же, как и в предыдущих случаях.
(((ab)c)d)e=(((ae)b)c)d+((a(be))c)d+((ab)(ce))d+((ab)c)(de)=(((ae)b)c)d-(((be)a)c)d+
+((a(ce))b)d+(a(b(ce)))d+((a(de))b)c+(a(b(de)))c+(ab)(c(de))=(((ae)b)c)d-(((be)a)c)d-
-(((ce)a)b)d+(((ce)b)a)d-(((de)a)b)c+(((de)b)a)c+(a(c(de)))b+a(b(c(de)))=(((ae)b)c)d-
-(((be)a)c)d-(((ce)a)b)d+(((ce)b)a)d-(((de)a)b)c+(((de)b)a)c+(((de)c)a)b-(((de)c)b)a
Получаем следующее равенство
abcde=aebcd-beacd-ceabd+cebad-deabc+debac+decab-decba
Найдем нетривиальные решения уравнения (3) для слов длины 5, придавая порождающим a, b, c, d, e только два значения а или b. Для случая  слов длины   5  будет 2⁵=32   комбинаций  присвоения всевозможными способами значений аили b.
Сведем все результаты вычислений в таблицу (см. таблицу 3).

Таблица 3

Выпишем из таблицы получившиеся равенства:
1)        (baba)a=(baab)a; (abba)a=(abab)a.    
2)        (abab)b=(abba)b,  (baab)b=(abba)b.
Данные равенства являются следствиями равенств, получившихся при рассмотрении  уравнений для слов длины 4. 
На основании этих данных можно сделать вывод, что  для  слов длины 5, уравнение (3)  нетривиальных решений не имеет.
Пусть L[a,b,с,d,e,f] – свободная алгебра Ли от 6-ти порождающих. Рассмотрим линейные комбинации правонормированных слов длины 6, линейных по каждому входящему в них символу.
((((ab)c)d)e)f=((((af)b)c)d)e+(((a(bf))c)d)e+(((ab)(cf))d)e+(((ab)c)(df))e+(((ab)c)d)(ef)
=((((af)b)c)d)e-((((bf)a)c)d)e+(((a(cf))b)d)e+((a(b(cf)))d)e+(((a(df))b)c)e+((a(b(df)))c)e
+((ab)(c(df)))e+((a(ef)b)c)d+((a(b(ef)))c)d+((ab)(c(ef)))d+((ab)c)(d(ef))=((((af)b)c)d)e-
-((((bf)a)c)d)e-((((cf)a)b)d)e+((((cf)b)a)d)e-((((df)a)b)c)e+((((df)b)a)c)e+((a(c(df)))b)e
+(a(b(c(df))))e-((((ef)a)b)c)d+((((ef)b)a)c)d+((a(c(ef)))b)d+(a(b(c(ef))))d
+((a(d(ef)))b)c+(a(b(d(ef))))c+((ab)(c(d(ef))))=((((af)b)c)d)e-((((bf)a)c)d)e
-((((cf)a)b)d)e+((((cf)b)a)d)e-((((df)a)b)c)e+((((df)b)a)c)e+((((df)c)a)b)e-
((((df)c)b)a)e-((((ef)a)b)c)d+((((ef)b)a)c)d+((((ef)c)a)b)d-((((ef)c)b)a)d+((((ef)d)a)b)c-((((ef)d)b)a)c-((((ef)d)c)a)b+((((ef)d)c)b)a
В итоге приходим к следующему равенству
abcdef = afbcde-bfacde-cfabde+cfbade-dfabce+dfbace+dfcabe-dfcbae –efabcd+ efbacd+efcabd-efcbad+efdabc-efdbac-efdcab+efdcba
Найдем хотя бы одно нетривиальное решение уравнения (3) для слов длины 6.  Так же как и в случае слов длины 5 будем придавать a, b, c, d, e, f  только два значения а или b. Пусть а:=а (а присвоено значение а), b:=b, c:=a, d:=a, e:=a, f:=b, тогда
abaaab = abbaaa-ababaa+abbaaa-ababaa+abbaaa+abaaba-ababaa-ababaa+
+abbaaa+abaaba-ababaa+abaaba-ababaa-abaaab+abaaba
Приведем подобные слова. В итоге получим:
2abbaaa-3ababaa+2abaaba=abaaab или (2abbaa-3ababa+2abaab)a=(abaaa)b
В предыдущем примере для слов длины 5 мы выявили равенства слов 
ababb=abbab,  baabb=abbab,   babaa=baaba,  abbaa=ababa.
Сделав замену, получаем    (2abaab-abbaa)a=(abaaa)b
Таким образом, получено нетривиальное решение уравнения (3) для слов длины 6:     =2abaab-abbaa; =abaaa
Так как уравнение вида xa=yb ранга 2 в свободной алгебре Ли L[a,b] для слов длин 3,5 нетривиальных решений не имеет, то естественно выдвинуть  гипотезу о том, что оно не будет иметь нетривиальных решений для слов нечетной длины.

1. Мальцев А.И. – Об уравнении   в свободной группе. // Алгебра и логика. – 1962. –  №5 – том 1. – C. 45-50.
2. Маканин Г.С. – Проблема разрешимости уравнений в свободной полугруппе. //Математический сборник. –  1977. – №2(6). – том 103(145). – С.147-236.
3. Маканин Г.С., Разборов А.А.  - Уравнение в свободной группе. // Изв.АН СССР. –  сер.матем. –  1982. –  № 6. – том 46. – C. 1199-1273.
4. Маканин Г.С., Разборов А.А. – Системы уравнений в свободной группе.           // Изв.АН СССР. –  сер.матем. – 1984. – № 4. – том 48. C. 779-832.
5. Шантаренко В.Г.  - Уравнения в свободной алгебре Ли  и аппроксимируемость свободными алгебрами Ли. //Препринт 6. – ИИТПМ СО РАН.  - Омск. –  1992. – C. 24.
6. Remeslennikov V.N., Stohr R.  - The equation [x,u]+[y,v]=0 in free Lie algebras. Internat. J. Algebra Comput.  - 17 (2007). –  no.5/6. – C. 1165-1187.
7. Демисенов Б.Н. – Идеалы свободных произведений алгебр Ли. //Деп. в ВИНИТИ. –  №1833-В94. – 1994. – C. 30.
8. Ширшов А.И. –  Подалгебры свободных лиевых алгебр. // Мат.сб. – 1953. –  №2. – т.33(75). – C. 471-472.

Все статьи автора «Сизова Ольга Алексеевна»