Определение всех используемых понятий, терминов и обозначений можно найти в работах  . Компакт – компактное хаусдорфово пространство, не обязательно метризуемое. Все пространства предполагаются вполне регулярными.
. Компакт – компактное хаусдорфово пространство, не обязательно метризуемое. Все пространства предполагаются вполне регулярными.
Одним из расширений класса диадических компактов  является класс
является класс  -адических пространств – пространств, допускающих счетное покрытие компактами, являющимися непрерывными образами
-адических пространств – пространств, допускающих счетное покрытие компактами, являющимися непрерывными образами 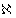 -метризуемых компактов (т.е.
-метризуемых компактов (т.е. 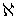 - адическими компактами) [5]. Структура и свойства пространств этого класса оказались тесно связанными с задачами продолжения непрерывных отображений. Описанию этих связей в общих случаях и в некоторых специальных ситуациях посвящена данная работа.
- адическими компактами) [5]. Структура и свойства пространств этого класса оказались тесно связанными с задачами продолжения непрерывных отображений. Описанию этих связей в общих случаях и в некоторых специальных ситуациях посвящена данная работа.
Лемма 1. Пусть 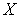 - топологическое пространство, причем любое каноническое замкнутое подмножество
- топологическое пространство, причем любое каноническое замкнутое подмножество 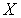 имеет тип
имеет тип 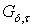 в
в  ,
, 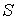 - всюду плотное подпространство
- всюду плотное подпространство 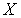 такое, что для любого замкнутого подмножества
такое, что для любого замкнутого подмножества  типа
типа 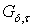 в
в 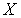 пересечение
пересечение 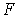 с
с 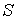 не пусто,
не пусто, 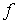 - непрерывное отображение
- непрерывное отображение 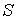 в пространство
в пространство 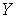 , причем
, причем 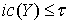 . Тогда существует непрерывное отображение
. Тогда существует непрерывное отображение 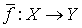 такое, что
такое, что 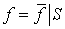 .
.
Доказательство. Для каждой точки  обозначим через
обозначим через 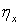 семейство всех замкнутых подмножеств
семейство всех замкнутых подмножеств 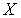 типа
типа 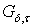 в
в 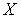 , содержащих эту точку. Ясно, что для любого
, содержащих эту точку. Ясно, что для любого 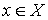 семейство
семейство  является
является 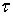 - центрированным Семейство
- центрированным Семейство 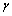 подмножеств пространства
подмножеств пространства 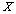 называется
называется 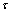 - центрированным, если для любого подсемейства
- центрированным, если для любого подсемейства 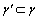 мощности
мощности 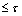 выполнено
выполнено 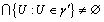 .. Положим
.. Положим 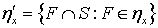 ,
, 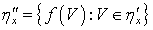 и
и 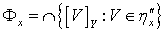 . Так как для любого подсемейства
. Так как для любого подсемейства 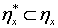 мощности
мощности 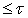 существует элемент
существует элемент 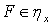 такой, что
такой, что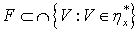 , то семейство
, то семейство 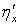 является
является 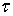 - центрированным для любого
- центрированным для любого 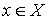 , а так как
, а так как 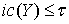 , то множество
, то множество 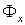 не пусто для любого
не пусто для любого  . Покажем, что для любого
. Покажем, что для любого 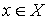 выполняется
выполняется 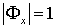 . Допустим, что существует точка
. Допустим, что существует точка 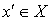 такая, что
такая, что 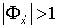 . Выберем различные точки
. Выберем различные точки  ,
, 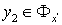 и окрестности
и окрестности 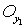 и
и 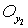 этих точек в
этих точек в 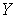 такие, что
такие, что 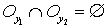 . Пусть
. Пусть 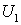 и
и 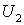 - открытые подмножества пространства
- открытые подмножества пространства 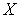 такие, что
такие, что  и
и 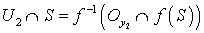 . Так как
. Так как 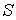 всюду плотно в пространстве
всюду плотно в пространстве 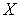 , то
, то 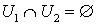 . Так как любое каноническое замкнутое подмножество
. Так как любое каноническое замкнутое подмножество 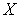 имеет тип
имеет тип 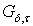 в
в 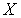 , то существуют открытые подмножества
, то существуют открытые подмножества 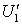 и
и 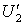 пространства
пространства 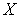 такие, что
такие, что 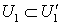 ,
, 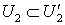 ,
, 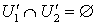 и замкнутые множества
и замкнутые множества 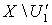 и
и 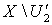 имеют тип
имеют тип 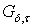 в пространстве
в пространстве 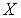 . В силу того, что
. В силу того, что 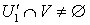 и
и 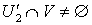 для любого элемента
для любого элемента 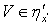 получаем, что
получаем, что 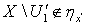 и
и 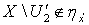 . Тогда
. Тогда 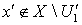 и
и 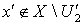 - получаем противоречие с тем, что
- получаем противоречие с тем, что 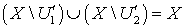 . Таким образом,
. Таким образом, 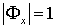 для любой точки
для любой точки 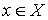 . Отображение, ставящее в соответствие каждой точке
. Отображение, ставящее в соответствие каждой точке 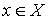 одноточечное множество
одноточечное множество 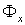 , обозначим через
, обозначим через 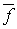 . Очевидно, что
. Очевидно, что 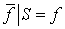 .
.
Покажем, что отображение 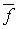 непрерывно. Пусть
непрерывно. Пусть  - произвольное открытое подмножество
- произвольное открытое подмножество 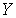 такое, что
такое, что 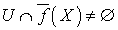 . Для каждой точки
. Для каждой точки 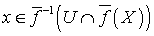 выберем окрестность
выберем окрестность 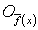 точки
точки  в
в  такую, что
такую, что 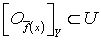 . Покажем, что
. Покажем, что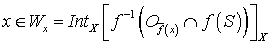 для любого
для любого 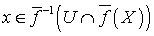 . Допустим, что существует точка
. Допустим, что существует точка 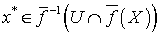 такая, что
такая, что  . Так как множество
. Так как множество 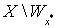 имеет тип
имеет тип 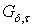 в
в 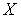 , то
, то 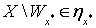 , что противоречит тому, что
, что противоречит тому, что 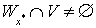 для любого элемента
для любого элемента 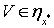 . Покажем, что для любого
. Покажем, что для любого 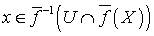 и любого
и любого 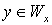 выполняется
выполняется 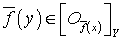 . Допустим, что существует точка
. Допустим, что существует точка 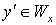 такая, что
такая, что 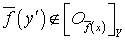 и рассмотрим окрестность
и рассмотрим окрестность 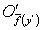 точки
точки 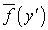 в
в  такую, что
такую, что 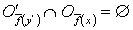 . Тогда
. Тогда 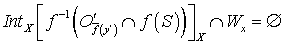 , что противоречит тому, что
, что противоречит тому, что 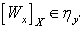 . Таким образом,
. Таким образом, 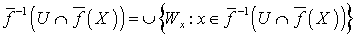 , т. е.
, т. е. 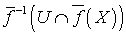 является открытым подмножеством пространства
является открытым подмножеством пространства 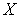 . Лемма доказана.
. Лемма доказана.
Теорема 1. Для того, чтобы финально компактное пространство 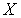 было
было 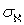 -диадическим необходимо и достаточно, чтобы оно являлось непрерывным образом открытого подмножества
-диадическим необходимо и достаточно, чтобы оно являлось непрерывным образом открытого подмножества 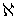 -метризуемого компакта.
-метризуемого компакта.
Доказательство. Доказательство необходимости проводится по стандартной схеме [5].
Достаточность. Пусть 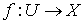 - непрерывное отображение открытого подмножества
- непрерывное отображение открытого подмножества 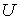
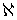 -метризуемого компакта
-метризуемого компакта  на финально компактное пространство
на финально компактное пространство  . Замыкание множества
. Замыкание множества 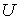 в
в 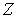 обозначим через
обозначим через 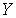 . Через
. Через 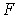 обозначим объединение всех замкнутых типа
обозначим объединение всех замкнутых типа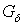 подмножеств
подмножеств 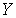 , лежащих в множестве
, лежащих в множестве 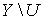 . Так как пространство
. Так как пространство 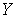 совершенно
совершенно 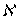 -нормально, то каждое каноническое замкнутое подмножество пространства
-нормально, то каждое каноническое замкнутое подмножество пространства  имеет тип
имеет тип 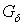 в
в 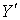 . Из леммы 1 следует, что существует непрерывное отображение
. Из леммы 1 следует, что существует непрерывное отображение 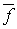 пространства
пространства 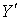 на
на 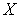 такое, что
такое, что 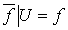 . Так как множество
. Так как множество 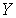 имеет тип
имеет тип 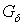 в
в 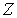 , то множество
, то множество 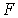 является объединением замкнутых подмножеств типа
является объединением замкнутых подмножеств типа  в
в 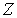 . Множество
. Множество 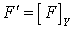 имеет тип
имеет тип 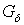 в
в 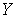 . Так как
. Так как 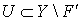 , то
, то 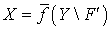 , а так как пространство
, а так как пространство 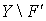 является
является 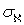 -адическим, то и пространство
-адическим, то и пространство 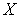 является
является 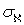 -адическим. Теорема доказана.
-адическим. Теорема доказана.
Теорема 2. Если псевдокомпактное пространство 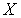 является непрерывным образом открытого подмножества
является непрерывным образом открытого подмножества 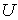
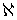 -метризуемого компакта
-метризуемого компакта 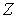 , то любое компактное хаусдорфово расширение
, то любое компактное хаусдорфово расширение 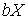 пространства
пространства 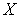 является
является  -адическим пространством.
-адическим пространством.
Доказательство. Пусть 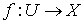 - непрерывное отображение
- непрерывное отображение 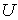 на
на 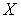 . Обозначим через
. Обозначим через  замыкание множества
замыкание множества  в
в 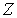 . Пусть
. Пусть 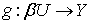 - стандартное отображение стоун-чеховской компактификации
- стандартное отображение стоун-чеховской компактификации 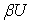 пространства
пространства 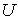 на
на 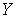 и
и 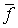 - непрерывное продолжение отображения
- непрерывное продолжение отображения 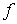 на
на 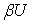 . Так как пространство
. Так как пространство 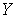 совершенно
совершенно 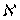 -нормально, то существует множество
-нормально, то существует множество 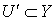 , содержащее
, содержащее 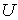 , такое, что множество
, такое, что множество 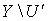 является объединением типа
является объединением типа  подмножеств
подмножеств 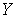 и
и 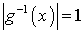 для любой точки
для любой точки  . Множество
. Множество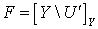 имеет тип
имеет тип 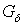 в
в 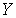 и, следовательно, множество
и, следовательно, множество 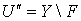 обладает счетным покрытием из
обладает счетным покрытием из 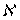 -адических компактов. Так как отображение
-адических компактов. Так как отображение 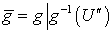 является гомеоморфизмом, то
является гомеоморфизмом, то 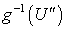
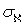 -адично, а так как
-адично, а так как 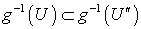 и пространство
и пространство 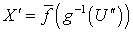 финально компактно, то
финально компактно, то 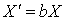 . Теорема доказана.
. Теорема доказана.
Лемма 2. Пусть 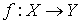 - непрерывное замкнутое отображение пространства
- непрерывное замкнутое отображение пространства 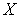 на компакт
на компакт 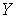 ,
, 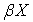 - стоун-чеховская компактификация пространства
- стоун-чеховская компактификация пространства 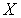 и
и 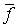 - непрерывное продолжение отображения
- непрерывное продолжение отображения  на
на 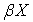 . Тогда для любого нормального подпространства
. Тогда для любого нормального подпространства  , содержащего
, содержащего 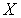 , отображение
, отображение  является замкнутым.
является замкнутым.
Доказательство. Пусть 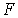 - произвольное замкнутое подмножество пространства
- произвольное замкнутое подмножество пространства 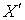 ,
,  и
и 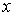 - произвольная точка множества
- произвольная точка множества 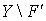 . Ясно, что
. Ясно, что 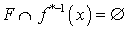 . Так как
. Так как 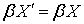 и пространство
и пространство 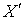 нормально, то
нормально, то 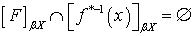 . Нетрудно показать, что
. Нетрудно показать, что
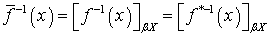 ,
,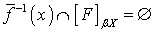 . Выберем открытое подмножество
. Выберем открытое подмножество 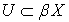 такое, что
такое, что 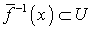 и
и 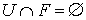 . Положим
. Положим 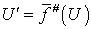 . Ясно, что
. Ясно, что 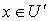 и
и 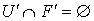 . Так как точка
. Так как точка  была выбрана произвольно, то
была выбрана произвольно, то 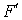 является замкнутым подмножеством пространства
является замкнутым подмножеством пространства 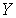 . Лемма доказана.
. Лемма доказана.Теорема 3. Компакт, являющийся образом открытого подмножества
 -адического компакта относительно непрерывного замкнутого отображения, является
-адического компакта относительно непрерывного замкнутого отображения, является 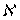 -адическим.
-адическим.Доказательство. Пусть компакт
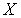 является непрерывным замкнутым образом открытого подмножества
является непрерывным замкнутым образом открытого подмножества  -адического компакта
-адического компакта 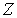 . Тогда
. Тогда  является непрерывным замкнутым образом некоторого открытого подмножества
является непрерывным замкнутым образом некоторого открытого подмножества 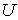 некоторого
некоторого 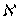 -метризуемого компакта
-метризуемого компакта 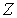 . Замыкание множества
. Замыкание множества 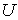 в
в 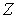 обозначим через
обозначим через 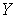 , непрерывное замкнутое отображение
, непрерывное замкнутое отображение 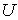 на компакт
на компакт  обозначим через
обозначим через 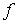 . Пусть
. Пусть 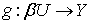 - стандартное отображение стоун-чеховской компактификации
- стандартное отображение стоун-чеховской компактификации 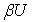 пространства
пространства 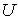 на
на 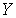 и
и 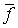 - непрерывное продолжение отображения
- непрерывное продолжение отображения 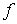 на
на 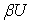 . Так как пространство
. Так как пространство 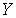 совершенно
совершенно 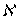 -нормально, то существует множество
-нормально, то существует множество 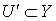 такое, что
такое, что  и
и 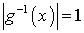 для любой точки
для любой точки 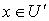 , причем множество
, причем множество 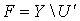 является объединением замкнутых типа
является объединением замкнутых типа 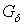 подмножеств пространства
подмножеств пространства 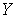 . Заметим, что множество
. Заметим, что множество 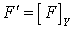 имеет тип
имеет тип 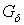 в
в 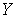 . Таким образом, открытое в
. Таким образом, открытое в 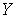 множество
множество 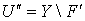 является финально компактным пространством, причем
является финально компактным пространством, причем 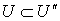 . Так как
. Так как 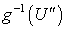 нормально, то из леммы 3 следует замкнутость отображения
нормально, то из леммы 3 следует замкнутость отображения 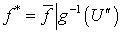 . Тогда существует компакт
. Тогда существует компакт  такой, что
такой, что 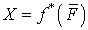 . Пусть
. Пусть 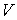 - каноническое замкнутое подмножество
- каноническое замкнутое подмножество 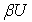 такое, что
такое, что 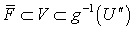 . Ясно, что
. Ясно, что 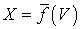 . Так как
. Так как  гомеоморфизм и
гомеоморфизм и 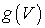 является
является 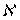 -адическим компактом, то
-адическим компактом, то 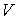 является
является 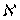 -адическим компактом. Отсюда, так как
-адическим компактом. Отсюда, так как 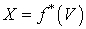 , то компакт
, то компакт 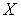 является
является 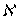 -адическим компактом. Теорема доказана.
-адическим компактом. Теорема доказана.Теорема 4. Компакт
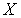 , являющийся образом открытого подмножества
, являющийся образом открытого подмножества 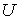
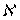 -адического компакта относительно непрерывного открытого отображения
-адического компакта относительно непрерывного открытого отображения 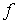 , является
, является  -адическим.
-адическим.Доказательство. Нетрудно показать, что существует замкнутое подмножество
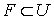 такое, что
такое, что 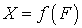 и отображение
и отображение 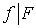 является совершенным. Так как компактность сохраняется при переходе к прообразам относительно совершенных отображений, то
является совершенным. Так как компактность сохраняется при переходе к прообразам относительно совершенных отображений, то 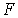 является компактном. Пусть
является компактном. Пусть 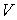 - каноническое замкнутое подмножество
- каноническое замкнутое подмножество 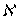 -адического компакта такое, что
-адического компакта такое, что 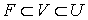 . Так как
. Так как 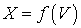 и
и 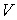 -
- 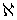 -адический компакт
-адический компакт 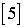 , то
, то 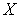 является
является 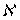 -адическим компактом. Теорема доказана.
-адическим компактом. Теорема доказана.Теорема 5. Если
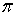 - вес
- вес 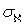 -адического компакта
-адического компакта 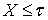 , то существует множество
, то существует множество 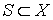 мощности
мощности  всюду плотное в
всюду плотное в 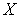 такое, что
такое, что  для любой точки
для любой точки  .
.Доказательство. Пусть
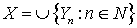 , где
, где 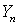 -
- 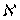 -адический компакт для любого
-адический компакт для любого 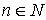 . Обозначим через
. Обозначим через 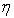
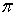 -базу пространства
-базу пространства 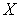 мощности
мощности 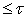 . Покажем, что в каждом элементе
. Покажем, что в каждом элементе 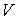 семейства
семейства 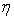 существует точка
существует точка 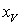 такая, что
такая, что 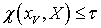 . Выберем элемент
. Выберем элемент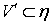 такой, что
такой, что 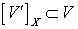 . Положим
. Положим 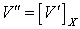 . Так как всякий компакт обладает свойством Бэра и
. Так как всякий компакт обладает свойством Бэра и  , то существуют открытое подмножество
, то существуют открытое подмножество 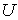 пространства
пространства  и номер
и номер 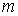 такие, что
такие, что  . Замыкание множества
. Замыкание множества 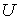 в
в 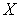 обозначим через
обозначим через 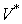 . Так как
. Так как 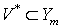 , то
, то 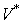 является
является 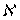 -адическим компактом. Так как для всякого
-адическим компактом. Так как для всякого 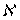 -адического компакта
-адического компакта 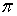 -вес совпадает с весом, то
-вес совпадает с весом, то 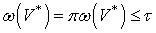 . Выберем произвольную точку
. Выберем произвольную точку 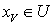 . Так как
. Так как  , а
, а 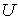 является открытым подмножеством пространства
является открытым подмножеством пространства 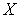 , то
, то 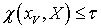 . Ясно, что множество
. Ясно, что множество 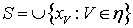 является искомым. Теорема доказана.
является искомым. Теорема доказана. Следствие. Если
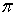 -вес
-вес 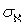 -адического компакта
-адического компакта 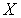 счетен, то
счетен, то 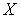 удовлетворяет первой аксиоме счетности на счетном всюду плотном подмножестве.
удовлетворяет первой аксиоме счетности на счетном всюду плотном подмножестве.Библиографический список
- Архангельский А.В. Об отображениях всюду плотных подпространств топологических произведений. // Докл. АН СССР, 1971. т. 197. № 4. С. 750 – 753.
- Широков Л.В. О продолжении непрерывных отображений и аппроксимативной связности // Проблемы современной науки, Центр научного знания «ЛОГОС».2013. выпуск 9. С. 3–9.
- Широков Л.В. Внешняя характеристика пространств Дугунджи и -метризуемых бикомпактов. // Докл. АН СССР. 1982. т. 263. № 5. С. 1073-1077.
- Широков Л.В. О AE(n)-компактах. //Известия РАН, 1992. т. 56. № 6. С. 1316 – 1327.
- Щепин Е.В. О - метризуемых пространствах. //Изв. АН СССР. Сер. матем, 1979. 43:2. С. 442–478.
- Ефимов Б.А. Диадические бикомпакты. // Труды Моск. Мат. Общ., 1965. т. 14. С. 211-247.
- Trukhmanov V.B. On subdirect sums of abelian torsion-free groups of rank 1. // Journal of Mathematical Sciences. 2008. Т. 154. № 3. С. 422-429.
- Трухманов В.Б. Подпрямые суммы абелевых групп без кручения ранга 1. // Фундаментальная и прикладная математика. 2007. Т. 13. № 3. С. 209-221.