Рассмотрим уравнение наблюдения вида: 
, 
где  – уравнение регрессии,  – случайная переменная (ошибка наблюдений),  и  ( –математическое ожидание),  – базисный вектор регрессии (непрерывные на области  функции, ),  – вектор входных переменных (размерности ),  – наблюдаемая переменная,  – неизвестные параметры модели. 
Наблюдения проводятся в точках  (спектра плана экспериментов, ) в количестве  в каждой из точек соответственно. Введем обозначения: , , , 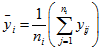. Тогда методом наименьших квадратов оценки параметров  находятся в соответствии с формулой: . 
План эксперимента (ПЭ) – называется набор из точек спектра и весов. В соответствии с этими весами общее число экспериментов  распределяется по этим точкам: 
, 
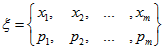где .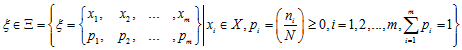
Задача построения оптимального ПЭ состоит в нахождении на множестве  такого, который максимизирует (минимизирует) функционал от некоторой характеристики оценок параметров модели.
Так, если ПЭ получается в соответствии с решением задачи максимизации критерия от матрицы Фишера , , то ПЭ называется -оптимальным [1]:
. (1)
Можно вместо задачи (1) решать эквивалентную ей задачу:
, (2)
где  – обратная матрица для матрицы . Она с точностью до некоторой постоянной величины является дисперсионной матрицей оценок параметров модели. Критерий оптимальности ПЭ  – выпуклый вниз функционал (на множестве матриц , ).
Введем в рассмотрение ПЭ (план предельного перехода):
, .
Здесь  – некоторое большое целое число, а точки спектра ПЭ образуют равномерную сетку на . Тогда, в качестве точек спектра начального ПЭ  могут быть выбраны координаты локальных максимумов функции = (см. рис. 1).
Использование метода предельного перехода (МПП) позволяет снизить вычислительные затраты по поиску спектра начального ПЭ  в сравнении с классическими алгоритмами построения оптимальных ПЭ [1].

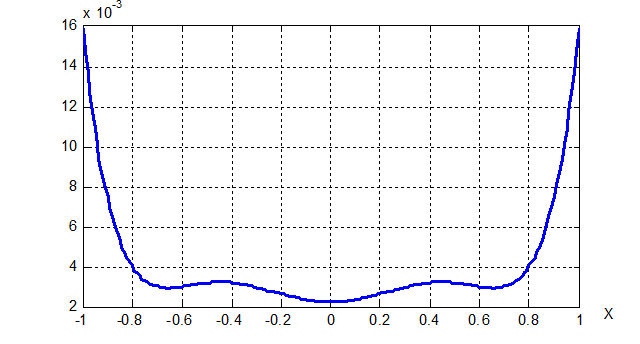Рисунок 1 – Функция  для критерия D-оптимальности;

модель с базисом , .

Пример. Построим начальный ПЭ для CI-критерия эффективности[2]: .
Этот критерий учитывает величину доверительного интервала оценок . Положим , . В качестве ПЭ предельного перехода выберем план , =1000. Тогда функцию  (аналог функции ) можно записать в виде [2]:
 
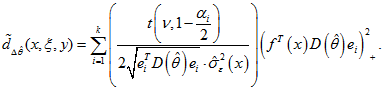
Выберем координаты точек локальных максимумов функции  в качестве точек спектра начального ПЭ. График функции  (с точностью до множителя ) приведен на рис. 2. Вычисления были проведены с использованием программы Kortanek_CI (см. текст программы в [2]).

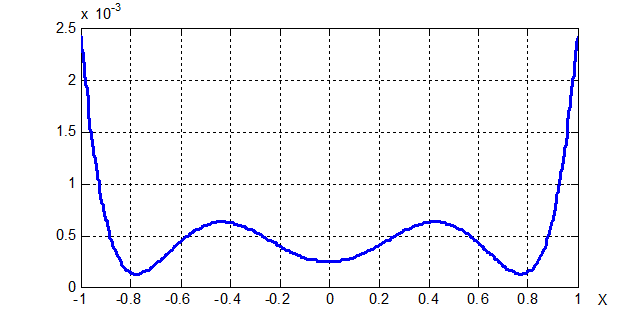
Рисунок 2 – График функции  для  на области  
при использовании ПЭ  и критерия .

На основе точек локальных максимумов функции  можно построить оптимальный ПЭ: .
Некоторые модификации метода МПП и примеры его использования при решении различных задач приведены в работах [2], [4] –[11].

Автор выражает признательность профессору К. Кортанеку за внимание к проведенному исследованию. МПП был предложен и апробирован после ознакомления с публикацией [3] (в то время – аспирантом кафедры Прикладной математики НГТУ). Заметим, что профессор К. Кортанек метод МПП в качестве метода для нахождения точек спектра ПЭ не рассматривал и не предлагал.

1. Федоров В.В. Теория оптимального эксперимента. М., 1971.
2. Наумов А.А., Сенич В.В. Введение в теорию управления экспериментом.  Новосибирск, 2004.
3. Gribik P.R., Kortanek K.O.  Equivalence Theorems and Cutting Plane Algorithms for a Class of Experimental Design Problems// SIAM Journal Appl. Math. 1977. № 1 (32). С. 232–259.
4. Наумов А.А. К асимптотическим свойствам эффективных стратегий экспериментирования// Научный вестник НГТУ. 2006. №. 1(22). С. 157–165.
5. Naumov A.A. Efficient Control of Experiments: Models and Algorithms// Proceedings 2005 Joint Statistical Meetings (JSM), August 7–11, 2005, ASA Section on Physical and Engineering Sciences. 2005. pp. 1748–1756.
6. Наумов А.А. Управление экспериментом и информация// Тез. докладов VI Всероссийской ФАМ конференции, 2-4 марта 2007 г., Красноярск,  ИЦ Института естественных и гуманитарных наук СФУ. 2007. С. 44–45.
7. Naumov A.A. Asymptotic Properties of Effective Experimenting Strategies// Proceedings 2006 Joint Statistical Meetings (JSM), August 6–10, 2006, Seattle, Washington, ASA Section on Statistical Computing. 2006. pp. 2125 – 2132.
8. Наумов А.А. Исследование свойств эффективных стратегий экспериментирования// Омский научный вестник. 2006. № 9 (46). С. 8–11.
9. Наумов А.А. CI-эффективное управление экспериментом. Ч. I//Научный вестник НГТУ. 2007. № 1(26). С. 31–38.
10. Наумов А.А. CI-эффективное управление экспериментом. Ч. II//Научный вестник НГТУ. 2007. № 2(27). С. 31–40.
11. Наумов А.А., Швабе Р., Рат В.В. Управление экспериментом в задачах диагностики// Сб.  статей  II-ой Международной научно-практической конференции, Международные и национальные особенности прикладной экономики, 4-5 декабря, 2008 г., Пенза. 2008. С. 23–26.
12.  Список трудов. [Электронный ресурс]. URL: https://sites.google.com/site/anatolynaumov2011/home/spisok-trudov-list-of-papers  (дата обращения 12.06.15).

Все статьи автора «Наумов Анатолий Александрович»