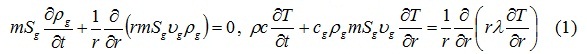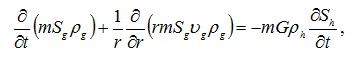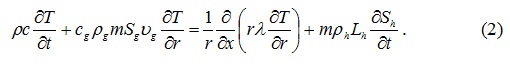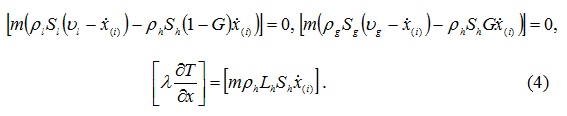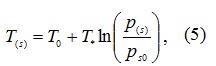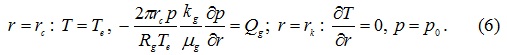В современном мире проблемы и задачи образования газовых гидратов являются актуальными и находят практическое приложение, поскольку имеются перспективы использования газовых гидратов в самых разных областях промышленности.

Один из вариантов использования описан Jadhawar P., Mohammadi A.H., Yang J., Tohidi B. в [1]. Авторы предлагают уменьшить объем парниковых газов путем их захоронения в виде газогидратов, что обеспечивает при малых затратах энергии высокий уровень безопасности захоронения.

При рассмотрении осесимметричной задачи предположим, что имеется однородный, горизонтальный пласт постоянной толщины и конечной протяженности. Пусть рассматриваемый пласт представляет собой пористую породу, которая в начальный момент частично заполнена газом и водой. Верхняя и нижняя граница пласта непроницаемы. В центре пласта пробурена скважина радиуса r = r_c, вскрывшая пласт на всю толщину. Через скважину закачивается тот же газ, что и в начале эксперимента, причем массовый расход Q_g на единицу высоты скважины остается постоянным, а температура равна Т_е.

В общем случае в результате нагнетания газа в пласт возникают три области, в которых газ, гидрат и вода находятся в различных состояниях. Соответственно, возникают две границы фазовых переходов, разделяющие данные области. В ближней области, примыкающей к скважине, в порах присутствуют газ и гидрат, а в порах дальней от скважины области – газ и вода. Промежуточная область, разделяющая ближнюю и дальнюю, содержит газ, гидрат и воду в состоянии термодинамического равновесия. При этом граница r = r_(n) разделяет ближнюю и промежуточную, а граница r = r_(d) – промежуточную и дальнюю области.

При инжекции газа происходят процессы теплопереноса и массопереноса, которые сопровождаются образованием газовых гидратов. Будем проводить описание этих процессов со следующими допущениями: пористость постоянна, скелет пористой среды, вода, газогидрат несжимаемы и неподвижны, газ калорически совершенный:

Здесь m – пористость,  и  - это истинная плотность и скорость j-ой (sk, l, h) фазы, p – давление, T – температура, R_g – газовая постоянная, индексы sk, l, g, h относятся, соответственно, к параметрам скелета пористой среды, воды, газа и гидрата. Кроме того, полагается, что при протекании процесса температура пористой среды и вещества, которое ее насыщает, т.е. газа, воды и гидрата, в каждой точке совпадают. Такой процесс носит название однотемпературного. Под гидратом имеется в виду двухкомпонентная система с массовой концентрацией газа G.

Система основных уравнений в осесимметричном случае для ближней и дальней областей имеет вид [2, 3]:

Для области, содержащей газ, гидрат и воду можно записать:

Закон Дарси можно записать в виде:

Условия на подвижных поверхностях фазовых переходов, следующие из баланса масс газа и воды, а также условия теплового баланса можно представить в виде:

Здесь [f] – скачок величины f на границе x=x_(s) между областями,  производная от x_(s) – скорость движения этой границы. Давление и температуру на этих поверхностях фазовых переходов будем считать непрерывными величинами.

В области совместного существования газа, гидрата и воды температура и давление на данной границе связаны условием фазового равновесия:

где T₀ – исходная температура системы, p_s0 – равновесное давление, которое соответствует начальной температуре, а T_* – некий эмпирический параметр, зависящий от вида газогидрата.

На скважине (r = r_(c)) и контуре питания (r = r_(k)) поставим следующие граничные условия:

В качестве начальных условий системы примем следующие параметры:

Для решения системы (1) и (2) с начальными и граничными условиями (6) и (7), а также условиями на поверхностях фазовых переходов (4), используем метод ловли фронта в узел пространственной сетки [2, 3, 4, 5]. Все расчеты были проведены для системы “пористая среда – твердый газогидрат – газ”, со следующими параметрами фаз: m=0.1, G=0.12, S_l0=0.2, k₀=10^-14 м², μ_g=10^-5 Па•с,  λ=2 Вт/(м×К), ρc=2.5∙10⁶ Дж/(К∙м³) , L_h=5×10⁵ Дж/кг, ρ_h=900 кг/м³, ρ_l=1000 кг/м³, T₀=280 K, T_*=10 K, p₀ =4 МПа p_s0=5.5 МПа, c_g=1560 Дж/(кг×К). При этом радиусы скважины и контура питания которого соответственно равны r_s = 0.1 м и r_k = 2.1 м.

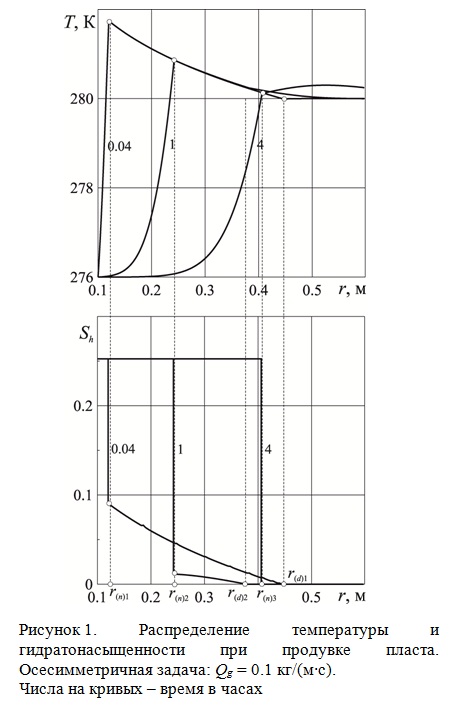
На рис. 1 представлены распределения температуры и гидратонасыщенности при нагнетании газа с массовым расходом Q_g = 0.1 кг/(м∙с). Как следует из рисунка, образование газогидрата в начальный момент времени происходит в протяженной области, которая затем, вырождается во фронтальную границу. Так в момент времени t = 0.1 ч координата дальней границы была равна r_(d)1 ≈ 0.45 м, а в момент времени t = 1 ч – r_(d)2 ≈ 0.37 м, что обусловленное сносом тепла вглубь пласта, образованного на поверхности x = x_(n), и разложением ранее образовавшегося гидрата. В момент времени t = 4 ч образование гидрата полностью происходит на фронтальной поверхности.

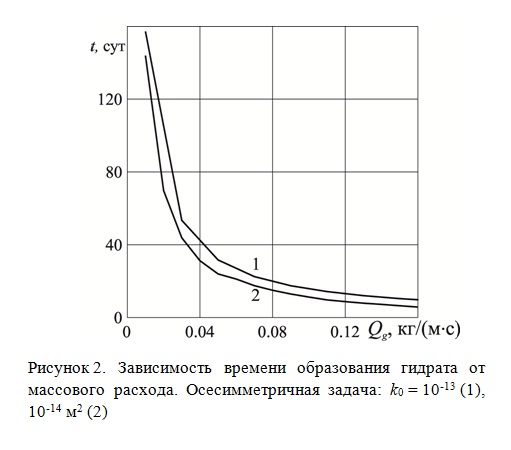
На рис. 2 для осесимметричного случая представлены зависимости времени образования гидрата в круговом пласте от массового расхода нагнетаемого газа. Линии 1 и 2 соответствуют значениям абсолютной проницаемости пласта k₀ = 10^-13 и 10^-14 м². Как видно из рисунка, с увеличением массового расхода время образования гидратов падает, что объясняется усилением потока от скважины вглубь пласта. Причем с уменьшением проницаемости это время, наоборот, уменьшается. Это объясняется тем, что при высокой проницаемости поток газа является более интенсивным, чем при низкой. Поэтому, в высокопроницаемых пластах величина давления на скважине и в самом пласте ниже, чем в низкопроницаемых.

Исследования выполнены при поддержке РФФИ, проект № 14-01-97032

1. Jadhawar P., Mohammadi A.H., Yang J., Tohidi B. Subsurface carbon dioxide storage through clathrate hydrate formation // Advances in the Geological Storage of Carbon Dioxide. Amsterdam: Springe, 2006. P. 111.
2. Хасанов М.К., Гималтдинов И.К., Столповский М.В. Особенности образования газогидратов при нагнетании холодного газа в пористую среду, насыщенную газом и водой // Теоретические основы химических технологий. 2010. Т. 44. №4. С.442 – 449.
3. Шагапов В.Ш., Хасанов М.К., Гималтдинов И.К., Столповский М.В. Особенности разложения газовых гидратов в пористых средах при нагнетании теплого газа // Теплофизика и аэромеханика. 2013. Т. 20. № 3. С. 347-454.
4. Васильев В.И., Попов В.В., Тимофеева Т.С. Вычислительные методы в разработке месторождений нефти и газа. – Новосибирск, 2000. – 127 с.
5. Кулаков П.А., Шишкина А.Ф., Кулакова А.Ф. Адаптивный алгоритм управления дозированием реагентов при производстве катионных нефтеполимерных смол // Современные проблемы науки и образования. – 2014. – № 4; URL: http://www.science-education.ru/118-14172 (дата обращения: 05.08.2014).

Все статьи автора «Шишкина Анна Федоровна»