Широкое применение регрессионного анализа в настоящее время обуславливается следующими факторами: быстрая смена изучаемых областей, которая не позволяет тратить много времени на исследования и получение требуемых зависимостей [1]. Регрессионный анализ может быть осуществлен даже в тех случаях, когда интерполяция невозможна из-за недостаточного размера выборки. Также можно использовать регрессионный анализ для проверки гипотез.
При использовании регрессионного анализа можно определить соответствие экспериментальных данных с предложенной теорией, описывающей изучаемый процесс.
Создание регрессионной модели – это последовательный процесс, который включает поиск эффективных независимых переменных для объяснения тех процессов, которые необходимо смоделировать или понять. Это управление инструментом регрессии для определения переменных, наиболее эффективных для предсказаний явлений, и, затем, удаление и добавление переменных с целью создания наилучшей модели для построения предположения. Регрессионный анализ позволяет учитывать теоретические аспекты, мнение авторов эксперимента, опробовавших данный метод при обработке результатов поставленных опытов; определить ожидаемую взаимосвязь между каждой потенциальной независимой переменной и зависимой величиной, еще до проведения самого анализа, а если эти связи не совпадают – задавать дополнительные вопросы и находить адекватные решения.
Регрессионный анализ помогает лучше понять причины происходящих процессов, чтобы иметь возможность сравнения теоретических и экспериментальных данных и принять правильное решение. Моделирование процессов позволяет лучше понять его суть, что может помочь выбрать меры, которые наиболее эффективны в данной ситуации [2].
Проблемами использования регрессионного анализа занимались многие ученые. В.В.Давнис предложил регрессионную модель, обеспечивающую воспроизведение процессов с динамикой случайных скачкообразных изменений и показал возможность использования модели для получения результатов предельного и энтропийного анализа риск-эффектов [3]. М.П.Кривенко рассмотрел задачи прогнозирования значений одной переменной по значениям другой методами регрессионного анализа [4]. В работе А.Е.Иохвидовой, С.Л.Подвального и Г.А.Остапенко рассматривается метод построения математической модели оценки риска информационно-телекоммуникационных систем, основанный на принципах множественного нелинейного регрессионного анализа [5]. А.Г.Кравцова в своей статье сделала попытку оценки использования нормального распределения в регрессионном анализе, а также указала направления проведения регрессионного анализа при нарушении некоторых предпосылок регрессионного анализа [6]. С.В.Алексиков рассмотрел методику обоснования производительности дорожно-строительных машин на основе регрессионного анализа [7]. Р.И.Баженов и др. применяли регрессионный анализ в различных предметных областях и программных средах [8-13]. Зарубежные ученые используют регрессионный анализ в своих исследованиях [14, 15].
Основной целью метода является определение количественной характеристики, которая описывает, как изменения, происходящие в одном или нескольких событиях (экспериментах), влияют на другое событие. Например, при описании деформированного состояния ледяного покрова от воздействия на него гидродинамических нагрузок следует учесть прогиб сплошного льда от скорости движения погруженного тела. Определение зависимости рассматриваемых характеристик от различных ледовых условий может помочь в прогнозирование ледоразрушающей способности, генерируемых нагрузкой системы прогрессивных волн, при определенной интенсивности которых может произойти частичное или полное разрушение льда [16].
Целью данной работы является нахождение зависимости максимального прогиба льда (ωmax), от скорости движения (v) распределенной нагрузки, составление таблицы экспериментальных значений этих величин, построение графика регрессионым анализом полиномами 2,3,4 степеней, определение полинома с наилучшей корреляцией, получение формулы зависимости этих величин, определение зависимых и независимых (объясняющих) переменных.
Регрессионная модель, построенная на основе теоретических данных [17] в программе Microsoft Excel (рис.1). На величину прогиба льда влияют физико-механические свойства льда (степень его солености, модуль упругости, предел прочности и т.д.), но определяющей величиной является скорость движения нагрузки.
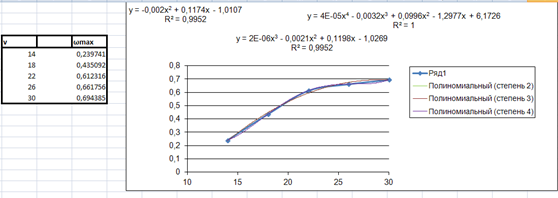
Рисунок 1 – График теоретической зависимости максимального прогиба льда от скорости движения нагрузки
На рис.1 показана зависимость максимального прогиба сплошного льда от скорости движения нагрузки, поскольку именно они свидетельствуют об однородности исследуемой информации.
Исходя из графика (рис.1) можем судить о нелинейной зависимости между рассматриваемыми параметрами и предположить, что зависимость будет полиноминальная.
Функции регрессионных моделей имеют вид:
y(x) = -0,002x2 + 0,1174x – 1,0107 (полином 2 степени)
R² = 0,9952 (коэффициент детерминации полинома 2 степени)
y(x) = 2E-06x3 – 0,0021x2 + 0,1198x – 1,0269 (полином 3 степени)
R² = 0,9952 (коэффициент детерминации полинома 3 степени)
y(x) = 0,0002x4 – 0,0148x3 + 0,4691x2 – 6,3099x + 30,806 (полином 4 степени)
R² = 0,9556 (коэффициент детерминации полинома 4 степени)
Возьмем экспериментальные данные величины прогиба (ωmax), и скорости (v) нагрузки из работы [18, 19] (рис.2) .
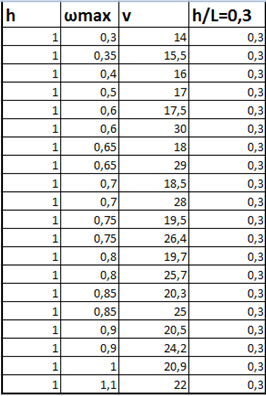
Рисунок 2 – Таблица зависимости экспериментальных данных величин максимального прогиба льда от скорости движения нагрузки
На основе данных таблицы (рис.2) можно построить в программе Microsoft Excel эмпирические линии регрессии полиномами (рис.3).
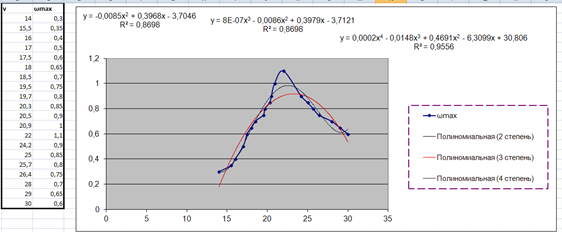
Рисунок 3 – Построение регрессии полиномами 2, 3, 4 степени
Функции регрессионных моделей будут иметь вид:
y(x) = -0,0085x2 + 0,3968x – 3,7046 (полином 2 степени)
R² = 0,8698 (коэффициент детерминации полинома 2 степени)
y(x) = 8E-07x3 – 0,0086x2 + 0,3979x – 3,7121 (полином 3 степени)
R² = 0,8698 (коэффициент детерминации полинома 3 степени)
y(x) = 0,0002x4 – 0,0148x3 + 0,4691x2 – 6,3099x + 30,806 (полином 4 степени)
R² = 0,9556 (коэффициент детерминации полинома 4 степени)
Из рис.3 видно, что график полинома 4 степени зависимости величины прогиба от скорости движения нагрузки, построенный по экспериментальным данным, имеет наибольший коэффициент детерминации.
Для более точного исследования на основе экспериментальных данных построим в программе Mathcad регрессионную модель (полиномом 4 степени) зависимости величины прогиба от скорости движения нагрузки (рис.4). Где x – величины прогибов, y – скорости движения нагрузки, vx – вектор независимых переменных, vy – вектор зависимых переменных, полиномиальная регрессия осуществляется с помощью встроенной функции regress(x,y,m), где m – полином 4 степени, kd2 – коэффициент детерминации, S- вектор результата (первые три строки являются служебными, а остальные содержат значения коэффициентов полинома.
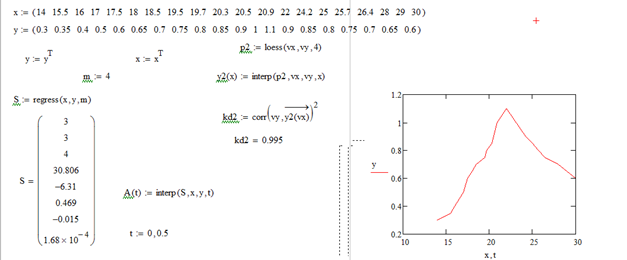
Рисунок 4 – Полиномиальная регрессия (полином 4 степени)
Таким образом, уравнение регрессионного полинома 4 степени будет иметь вид:
y(x) = 0,000168x4 – 0,015x3 + 0,469x2 – 6,31x + 30,806 (полином 4 степени)
kd2=0,995 (коэффициент детерминации)
Полученные результат зависимости максимального прогиба от скорости нагрузки, построенного по экспериментальным данным достаточно точно совпадает с графиком, построенным на основе теоретических данных. Это подтверждает правильность предложенной теории разрушения ледянных покровов при движении нагрузки. Из этого следует, что уравнение регрессионного полинома 4 степени с наибольшим коэффициентом детерминации поможет в прогнозировании ледоразрушающей способности генерируемых волн.
Библиографический список
-
Радченко С.Г. Методология регрессионного анализа. К.: Корнійчук, 2011. 376 с.
-
Кривенко М.П. Сравнительный анализ процедур регрессионного анализа информатика и ее применения // М.: Институт проблем информатики РАН. 2014. С. 70-78.
-
Давнис В.В. Использование регрессионных моделей в факторном анализе рисков // Современная экономика: проблемы и решения. 2011. № 8 (20). С. 96-102.
-
Кривенко М.П. Сравнительный анализ процедур регрессионного анализа // Институт проблем информатики Российской академии наук. 2014. № 8 (3). С. 70-78.
-
Иохвидова А.Е., Подвальный С.Л., Остапенко Г.А. Анализ риска информационно-телекоммуникационных систем на основе множественного нелинейного регрессионного анализа // Информация и безопасность. 2006. № 9 (2). С. 52-59.
-
Кравцова А.Г. Значение нормального распределения в регрессионном анализе // депонированная рукопись, 247-В2004, ВИНИТИ РАН, 12.02.2004, 14 с.
-
Алексиков С.В. Обоснование производительности дорожно-с троительных машин на основе регрессионного анализа // Вестник Волгоградского государственного архитектурно-строительного университета, строительство и архитектура. 2007. № 8. С. 78-80.
-
Пронина О.Ю., Баженов Р.И. Исследование методов регрессионного анализа программной среды eviews // Nauka-Rastudent.ru. 2015. № 1 (13). С. 45.
-
Лагунова А.А., Баженов Р.И. Разработка в среде gretl регрессионной модели рынка вторичного жилья г. Биробиджана // Nauka-Rastudent.ru. 2015. № 1 (13). С. 40.
-
Муллинов Д.О., Баженов Р.И. Разработка в среде eviews регрессионной модели рынка гаражных помещений г. Биробиджана // Nauka-Rastudent.ru. 2015. № 1 (13). С. 43.
-
Муллинов Д.О., Винокуров А.С., Баженов Р.И. Разработка в среде SPSS регрессионной модели рынка автомобилей // Nauka-Rastudent.ru. 2015. № 6.
-
Пивенко К.А., Баженов Р.И. Построение регрессионной модели в среде gretl на примере рынка поддержанных автомобилей г. Биробиджана и г. Хабаровска // Экономика и менеджмент инновационных технологий. 2015. № 4-1 (43). С. 72-80.
-
Эм А.А., Баженов Р.И. Разработка в среде eviews регрессионной модели реализации продукции компании по производству резинометаллических изделий // Экономика и менеджмент инновационных технологий. 2015. № 4-2 (43). С. 58-709.
-
Yang Y. Development of the regional freight transportation demand prediction models based on the regression analysis methods //Neurocomputing. 2015. Т. 158. С. 42-47.
-
Fumo N., Biswas M. A. R. Regression analysis for prediction of residential energy consumption //Renewable and Sustainable Energy Reviews. 2015. Т. 47. С. 332-343.
-
Козин В.М., Земляк В.Л. Физические основы разрушения ледяного покрова резонансным методом // Комсомольск-на-Амуре: ИМиМ ДВО РАН, ПГУ им. Шолом-Алейхема, 2013. 249 с.
-
Kozin V.M., Zemlak V.L., Chizhiumov S.D. Mathematical Model of Ice Sheet Deformation Caused by Submarine Motion // Proceedings of the International Offshore and Polar Engineering Conference 20th International Offshore and Polar Engineering Conference, ISOPE-2010, China National Offshore Oil Corporation (CNOOC), SK Energy. Beijing, 2010. С. 1171-1176.
-
Козин В.М., Чижиумов С.Д., Земляк В.Л. Исследование влияния ледовых условий на эффективность резонансного способа разрушения ледяного покрова, реализуемого подводными судами // Прикладная механика и техническая физика. 2010. Т. 51. № 3 (301). С. 118-125.
-
Земляк В.Л., Баурин Н.О., Курбацкий Д.А. Лаборатория «Ледотехники» // Вестник Приамурского государственного университета им. Шолом-Алейхема. 2013. № 1 (12). С. 068-077.


