Как было показано в [1], чтобы разработать модель распределения электронной концентрации (ЭК) неоднородной возмущенной ионосферы и на ее основе объяснить характер изменения дискретно-диффузной многолучевости, определяющей качественные показатели однолучевого декаметрового (ОДКМ) канала связи (КС), необходимо учесть следующие обстоятельства:
1. Известную модель распределения ЭК с учетом влияния ионосферных неоднородностей при нормальной ионосферы (НИ) и особенности проявления естественных возмущений.
2. Распределение ЭК в НИ является совокупностью изменения по высоте ее среднего значения ![]() и пространственных флуктуаций
и пространственных флуктуаций ![]() в неоднородностях
в неоднородностях
(1)
3. Среднеквадратическое отклонение (СКО) относительного значения флуктуаций ЭК по сравнению со средней ЭК ![]() , называемое интенсивностью неоднородностей
, называемое интенсивностью неоднородностей ![]() , на высотах
, на высотах ![]() км примерно постоянно и определяется выражением вида
км примерно постоянно и определяется выражением вида
(2)
.gif)
Тогда согласно (2) СКО абсолютного значения ![]() в слое F
в слое F ![]() намного больше, чем в поглощающих слоях D и E и возрастает по мере приближения к высоте h = hm с максимальной средней ЭК
намного больше, чем в поглощающих слоях D и E и возрастает по мере приближения к высоте h = hm с максимальной средней ЭК ![]() . Следовательно, изменение средней ЭК слоя F2 при естественном возмущении ионосферы (ЕВИ) влечет за собой изменение пространственных флуктуаций ЭК в неоднородностях. С учетом этого обстоятельства, выражение (1) можно представить в виде
. Следовательно, изменение средней ЭК слоя F2 при естественном возмущении ионосферы (ЕВИ) влечет за собой изменение пространственных флуктуаций ЭК в неоднородностях. С учетом этого обстоятельства, выражение (1) можно представить в виде
(3)
![]()
где ![]() - отклонение средней ЭК при ЕВИ от среднего значения ЭК в НИ,
- отклонение средней ЭК при ЕВИ от среднего значения ЭК в НИ, ![]() - отклонения пространственных флуктуаций ЭК в неоднородностях ионосферы при ее возмущениях.
- отклонения пространственных флуктуаций ЭК в неоднородностях ионосферы при ее возмущениях.
Для сравнительной оценки величины отклонений средней ЭК и пространственных флуктуаций возмущенной ионосферы выражение (3) представим в виде, аналогичном (2.1)
(4)
.gif)
где 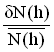 - вариации среднего значения ЭК возмущенной ионосферы относительно среднего значения ЭК в отсутствии возмущений,
- вариации среднего значения ЭК возмущенной ионосферы относительно среднего значения ЭК в отсутствии возмущений, .gif) - вариации среднего значения пространственных флуктуаций ЭК в неоднородностях ионосферы при естественных возмущениях.
- вариации среднего значения пространственных флуктуаций ЭК в неоднородностях ионосферы при естественных возмущениях.
Второе слагаемое в (4) ![]() количественно оценивается его СКО, которое можно выразить через коэффициент вариаций критических частот
количественно оценивается его СКО, которое можно выразить через коэффициент вариаций критических частот ![]() .
.
Учитывая выражение
где ![]() - критическая частота ионосферного слоя,
- критическая частота ионосферного слоя, ![]() - угол падения радиоволны на нижнюю границу ионосферы и выражение
- угол падения радиоволны на нижнюю границу ионосферы и выражение
.gif)
где ![]() - текущее значение критической частоты слоя F2,
- текущее значение критической частоты слоя F2, ![]() - среднее значение критической частоты,
- среднее значение критической частоты, ![]() - СКО критической частоты слоя F2 при ЕВИ можно представить как
- СКО критической частоты слоя F2 при ЕВИ можно представить как
(5)
.gif)
где ![]() - СКО величины
- СКО величины ![]() .
.
Согласно экспериментальным данным [2,3,4], коэффициент вариаций критических частот среднеширотной ионосферы ![]() при ЕВИ может изменяться на (20…40%), хотя могут быть возмущения, когда вариации указанного коэффициента могут достигать 100 %.
при ЕВИ может изменяться на (20…40%), хотя могут быть возмущения, когда вариации указанного коэффициента могут достигать 100 %.
Третье слагаемое в (4) .gif) количественно оценивается его СКО (интенсивностью неоднородностей
количественно оценивается его СКО (интенсивностью неоднородностей ![]() ) и определяется выражением (2).
) и определяется выражением (2).
Для количественной оценки четвертого слагаемого .gif) , в выражении (4) проанализируем сначала относительное значение флуктуаций ЭК
, в выражении (4) проанализируем сначала относительное значение флуктуаций ЭК ![]() по сравнению со средней
по сравнению со средней ![]() с учетом их отклонений
с учетом их отклонений ![]() и
и ![]() при ЕВИ
при ЕВИ
(6)
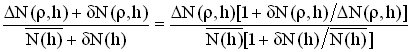
Согласно (2) в условиях НИ величина СКО относительного значения ![]() на любой высоте остается неизменной
на любой высоте остается неизменной
.gif)
Выражение (6) существенно упрощается, если исходить из следующего допущения: СКО относительного значения флуктуаций ЭК по сравнению со средней (т.е. фона) остаются постоянными не только при отсутствии ЕВИ (т.е.![]() ), но и при их наличии (
), но и при их наличии (![]() )
)
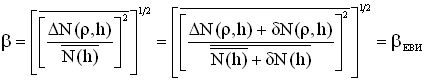
Согласно (6) введенное допущение ![]() справедливо при выполнении равенства
справедливо при выполнении равенства
(7)
Тогда четвертое слагаемое в (4) можно представить как
(8)
.gif)
С учетом равенства (7) выражение (8) сводится к виду
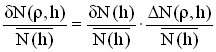
Отсюда СКО четвертого слагаемого (4), которое назовем коэффициентом вариаций пространственных флуктуаций ЭК в неоднородностях ионосферы при ЕВИ (![]() ), с учетом (2) и (5) выражается как
), с учетом (2) и (5) выражается как
(9)
.gif)
поскольку отклонения средней ЭК при ЕВИ ![]() и пространственные флуктуации ЭК в отсутствие ЕВИ
и пространственные флуктуации ЭК в отсутствие ЕВИ ![]() статистически независимы.
статистически независимы.
На рисунке 1 представлена модель распределения ЭК и ее пространственных флуктуаций в неоднородностях при наличии ЕВИ, соответствующая выражениям (3) и (4).
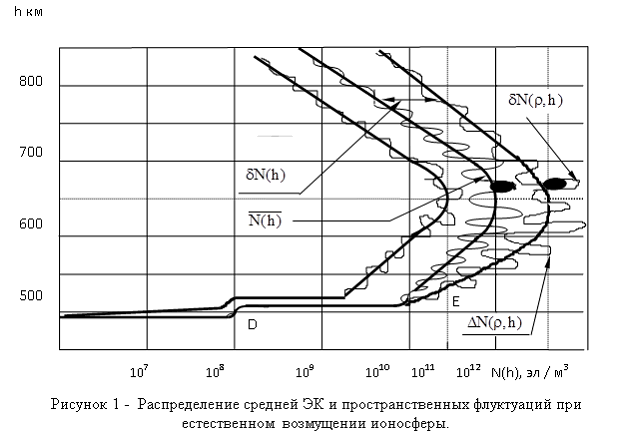
Данная модель отличается от используемой в настоящее время (1) дополнительным учетом вариаций средней ЭК ![]() и пространственных флуктуаций ЭК в неоднородностях ионосферы
и пространственных флуктуаций ЭК в неоднородностях ионосферы ![]() при ее возмущениях. На рисунке 1 затемненные области характеризуют различную степень пространственных флуктуаций ЭК в неоднородностях ионосферы. При этом с увеличением значения средней ЭК во время положительных возмущений увеличивается степень ее пространственных флуктуаций в неоднородностях и наоборот для отрицательных возмущений.
при ее возмущениях. На рисунке 1 затемненные области характеризуют различную степень пространственных флуктуаций ЭК в неоднородностях ионосферы. При этом с увеличением значения средней ЭК во время положительных возмущений увеличивается степень ее пространственных флуктуаций в неоднородностях и наоборот для отрицательных возмущений.
Благодаря полученным аналитическим выражениям для количественной оценки указанных вариаций с помощью коэффициентов ![]() (5) и
(5) и ![]() (9), разработанная модель является основой для построения математической модели ОДКМ КС в условиях ЕВИ. Достоверность модели косвенно подтверждается имеющимися результатами экспериментов по исследованию возмущенной ионосферы, приведенными в [3,4,5]. Достоверность полученных аналитических выражений (3) и (4) обусловлена тем, что в случае отсутствия ЕВИ они сводятся к зависимости (1), определяющей распределение ЭК в НИ.
(9), разработанная модель является основой для построения математической модели ОДКМ КС в условиях ЕВИ. Достоверность модели косвенно подтверждается имеющимися результатами экспериментов по исследованию возмущенной ионосферы, приведенными в [3,4,5]. Достоверность полученных аналитических выражений (3) и (4) обусловлена тем, что в случае отсутствия ЕВИ они сводятся к зависимости (1), определяющей распределение ЭК в НИ.
Таким образом, разработанная модель ЭК, описываемая выражениями (3,4,5,9) позволяет перейти к разработке многолучевой модели РДВ возмущенной ионосферы.
Библиографический список
- Антонов В.В., Павлюк Д.Н. Подход к разработке модели распределения электронной концентрации естественно возмущенной ионосферы // Исследования в области естественных наук. 2015. № 2 [Электронный ресурс]. URL: http://science.snauka.ru/?p=9004.
- Черенкова Е.Н., Чернышев О.В. Распространение радиоволн. – М.: Радио и связь, 1984. - 272 с.
- Ионосферные возмущения и их влияние на радиосвязь. / Ответственные редакторы Зевакина Р.А., Ляхова Л.Н. – М.: АН. СССР, 1971. – 239 с.
- Сомов А.М., Старостин В.В. Распространение радиоволн – М: Издательство «Гелиос АРВ», 2010 г. – 264 стр.
- Долуханов М.П. Флуктационные процессы при распространении радиоволн. – М.: Связь, 1971. – 183 с.
- Ткачук Р.В., Горденко Д.В., Павлюк Д.Н., Малофей А.О. Активная безопасность на основе криптографического мультинейропроцессора обработки данных. //Известия высших учебных заведений. Северо-Кавказский регион. Серия: Технические науки//. 2007.№ 4. С. 17-18.
- Горденко Д.В., Горденко Н.В., Павленко Н.А., Павлюк Д.Н., Ткачук Р.В. Коррекция ошибок в системе остаточных классов с минимальной временной сложностью на основе метода расширения оснований.//Известия высших учебных заведений. Северо-Кавказский регион. Серия: Технические науки//. 2007.№ 4. С. 12-14.
- Авторское свидетельство СССР N 1601672, кл. H 01G 15/16, 1988.
- Павлюк Д.Н., Горденко Д.В., Кондрашов А.В. Алгебра полиномов в цифровой фильтрации // Исследования в области естественных наук. 2015. № 2 [Электронный ресурс]. URL: http://science.snauka.ru/2015/02/8915


