Способность системы остаточных классов (СОК) поддерживать высокоскоростную арифметику при параллельной обработке данных является одним из путей повышения производительности вычислительных устройств. Система остаточных классов представляет собой такую систему, в которой целое положительное число представляется в виде набора остатков по выбранным основаниям [1]
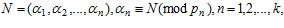 (1)
(1)
где pn – основания системы остаточных классов.
Система остаточных классов является альтернативой позиционной системе счисления, обладающая максимальным распараллеливанием выполнения арифметических операций. Между нейронной сетью и системой остаточных классов существует интересная связь. Если количество синапсов, используемых между нейронами, согласовано с количеством оснований СОК, то нейронная сеть становится натуральным представлением СОК.
Применение модулярного кодирования информации (использование системы остаточных классов) обусловлено прежде всего адекватностью СОК и нейронных сетей, которое заключается в следующем:
1. Семантическое сходство КТО и нейрона:
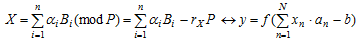 .
.
2. Выполнение арифметических операций с СОК может быть сопоставлено многослойной нейронной сети.
3. Основные операции нейросетевого логического базиса {+,×} просто реализуются в СОК.
4. Кодирование информации в СОК адекватно ассоциативной нейронной памяти, если сопоставить основание СОК классификационному признаку, а остаток – значению этого признака.
Таким образом, предлагается соединить возможности непозиционных модулярных кодов СОК и нейронные способы обработки информации.
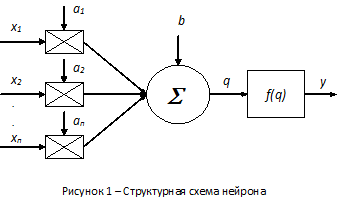
В качестве вычислительного средства для реализации вычислений в СОК может быть использован нейрокомпьютер (НК) как мощное вычислительное средство с массовым параллелизмом, поэтому возникает задача сопряжения модулярных и позиционных вычислительных устройств на основе нейронной сети (НС) [2]. Нейронная сеть является специфической параллельной вычислительной структурой и характеризуется большим числом связей, идущих к каждому процессорному элементу (нейрону). Основная модель нейрона – формальный нейрон или линейный пороговый элемент (рис. 1), определяемый соотношением (2).
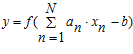 , (2)
, (2)
где x=(x1, x2, …, xN) – входной сигнал нейрона; a=(a1, a2, …,aN) – набор весовых коэффициентов; N – размерность входного сигнала; b – значение смещения (пороговый параметр нейрона); 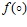 - функция активации; y – выходной сигнал.
- функция активации; y – выходной сигнал.
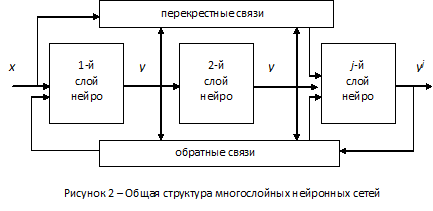
Нейроны объединяются в слои. Слой представляет собой совокупность нейронов с единым входным сигналом, не имеющих связей между собой. Ф. Розенблатом впервые были рассмотрены многослойные НС (рис. 2), где элементы (нейроны) в каждом слое находятся в равноправном топологическом отношении к элементам этого слоя, причем характер связи между слоями элементов может быть различным.
Уже доказано, что нейронный базис универсален, для любого алгоритма можно построить НС, которая его реализует. Но в настоящее время основное внимание уделяется разработке специализированных НК, ориентированных на решение задач, с которыми плохо справляются вычислительные средства прошлых поколений. Многие из этих задач можно свести к следующей обобщенной математической постановке: в соответствии с входным сигналом Х сформировать требуемый выходной сигнал Y. Отображение X®Y часто представляют множеством пар входных – выходных векторов {(Xk, Yk), k=1, 2, …, K}.
Для определения значений параметров НС используется алгоритм обучения. Если в необученную сеть ввести входной сигнал одного из примеров обучающей выборки, то выходы НС будут отличаться от требуемых выходов.
Функция ошибки определяет степень близости выходов НС к требуемым выходам при решении всей совокупности примеров обучающей выборки. Обучение – это итерационная процедура. На каждой итерации происходит уменьшение функции ошибки.
Выходной сигнал нейрона может посылаться другим элементам по взвешенным связям, с каждой из которых связан весовой коэффициент или вес. В зависимости от значения весового коэффициента передаваемый сигнал или усиливается, или подавляется. Нелинейная функция F называется активационной и может иметь различный вид [3].
Недостатком СОК является перекодирование слова из позиционной системы счисления в непозиционную систему и обратно.
В работе рассмотрен общий подход применению НС прямого распространения для преобразования чисел представленных в позиционном коде в систему остаточных классов. Данная нейронная сеть (рис. 3) представляет собой многослойную сеть, состоящая из входного слоя, скрытого и выходного слоя.
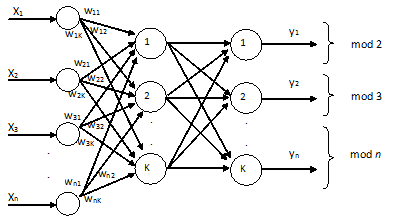
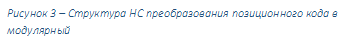
Входной слой нейронных элементов выполняет распределительные функции. Выходной слой нейронов служит для обработки информации от предыдущих слоев. Как и выходной слой, скрытый слой является обрабатывающим. Выход каждого нейронного элемента предыдущего слоя нейронной сети соединен синаптическими связями со всеми входами нейронных элементов следующего слоя. На этапе функционирования каждый нейрон выполняет свою функцию – передачу возбуждения другим нейронам – ровно один раз. Динамика состояний нейронов является безитерационной [4].
Таким образом, топология многослойной нейронной сети является однородной и регулярной. Выходы НС представляют собой остатки представленные в двоичном коде по заданным основаниям.
Основной принцип работы нейронной сети состоит в настройке параметров нейрона таким образом, чтобы поведение сети соответствовало некоторому желаемому поведению [5]. При настройке параметров нейрона использовалась логистическая функция активации (logsig). Ее аргумент может принимать любое значение в диапазоне от 0 до 1. Благодаря свойству дифференцируемости эта функция часто используется в сетях с обучением на основе метода обратного распространения ошибки.
Качество обучения сети с прямой передачей сигнала на выбранной обучающей последовательности поясняется на рис. 4. Практически нулевая точность достигается за 27 циклов обучения.
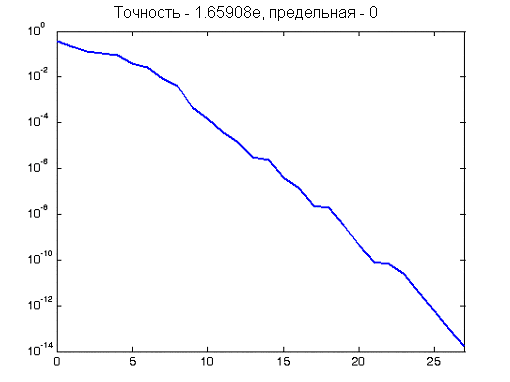
Рисунок 4 – График изменения ошибки обучения в зависимости от числа выполненных циклов
В заключении можно сделать вывод. Основываясь на свойствах нейронной сети прямого распространения, представленная сеть способна осуществлять любое отображение входных векторов в выходные. Сеть позволяет просто и эффективно решить задачу преобразования чисел представленных в позиционной системе счисления в модулярный код.
Достоинства сети: невысокая емкость, вместе с тем легкость построения программных и аппаратных моделей для многих практических применений.
Библиографический список
- Горденко Д.В., Резеньков Д.Н., Яйлаханов С.В. Высоконадежные комплексы и средства связи на нейросетевых элементах. – Москва, 2010.
- Горденко Д.В., Токарева Г.В. Принципы построения модулярных отказоустойчивых специализированных процессоров для обработки экономической информации. //Актуальные проблемы развития агробизнеса в условиях модернизации экономики// – Ставрополь, 2012. С. 71-77.
- Горденко Д.В., Горденко Н.В., Павленко Н.А., Павлюк Д.Н., Ткачук Р.В. Коррекция ошибок в системе остаточных классов с минимальной временной сложностью на основе метода расширения оснований.//Известия высших учебных заведений. Северо-Кавказский регион. Серия: Технические науки//. 2007.№ 4. С. 12-14.
- Горденко Д.В., Пономаренко М.В. Применение AN-кодов для коррекции ошибок в модулярных нейрокомпьютерах в области экономики.//Актуальные проблемы развития агробизнеса в условиях модернизации экономики.// – Ставрополь, 2012. С. 78-82.
- Калмыков И.А., Резеньков Д.Н., Горденко Д.В., Саркисов А.Б. Методы и алгоритмы реконфигурации непозиционных вычислительных структур для обеспечения отказоустойчивости спецпроцессов. – Ставрополь, 2014.
- Ткачук Р.В., Горденко Д.В., Павлюк Д.Н., Малофей А.О. Активная безопасность на основе криптографического мультинейропроцессора обработки данных. //Известия высших учебных заведений. Северо-Кавказский регион. Серия: Технические науки//. 2007.№ 4. С. 17-18.
- Горденко Д.В., Горденко Н.В. Локализация ошибок в устройствах цифровой обработки сигналов на основе алгебры полиномов.//Вестник СевКавГТИ//. 2009. № 9. С. 56-61.
- Горденко Д.В., Резеньков Д.Н., Сапронов С.В. Нормированный след полинома в процедурах поиска и локализации ошибок в модулярных кодах.// Вестник СевКавГТИ//. 2010. № 10. С. 72-73.
- Горденко Д.В., Горденко Н.В. Нейронная реализация локализации ошибок в модулярном коде.//Исследования в области естественных наук//. 2013. № 7 (19). С. 1.
- Червяков Н.И., Горденко Д.В. Нейронная сеть для округления и масштабирования чисел, представленных в системе остаточных классов.//Патент на изобретение RUS 2271570 26.05.2003//
- Червяков Н.И., Горденко Д.В., Сивоплясов Д.В., Ткачук Р.В. Модулярный сопроцессор для обработки биометрической информации.//Известия Южного федерального университета. Технические науки//. 2003. № 4 (33). С. 240-242.
- Горденко Д.В. Принципы построения модулярных отказоустойчивых специализированных процессоров для обработки информации.//Исследования в области естественных наук//. 2013. № 8 (20). С. 1.
- Горденко Д.В., Токарева Г.В. Нейронная сеть для преобразования чисел, представленных в позиционном коде в систему остаточных классов.// Информационные системы и технологии как фактор развития экономики региона//. 2013. С. 60-63.
- Горденко Д.В., Горденко Н.В. Нейронная сеть Хэмминга для преобразования модулярного кода в позиционный.//Исследования в области естественных наук//. 2013. № 11 (23). С. 5.
- Горденко Д.В. Перспективное развитие вычислительной техники на основе непозиционного нейрокомпьютера.//Исследования в области естественных наук//. 2013. № 12 (24). С. 3.
- Горденко Д.В., Резеньков Д.Н., Кондрашов А.В. Модулярные нейронные сети в автоматизированных системах управления.//Культура и общество: история и современность материалы II Всероссийской (с международным участием) научно-практической конференции. под редакцией: Колосовой О.Ю., Гударенко Р.Ф., Ряснянской Н.А., Красиковой Е.А.//. 2013. С. 63-67.
- Горденко Д.В., Горденко Н.В. Неисправности в запоминающих устройствах и в нейронных сетях.// Культура и общество: история и современность материалы II Всероссийской (с международным участием) научно-практической конференции. под редакцией: Колосовой О.Ю., Гударенко Р.Ф., Ряснянской Н.А., Красиковой Е.А.//. 2013. С. 67-70.
- Горденко Д.В., Резеньков Д.Н. Сравнительный анализ метода контроля арифметических операций в системе остаточных классах.// Современные проблемы науки и образования//. 2014. № 3. С. 148.
- Кондрашов А.В., Горденко Д.В., Резеньков Д.Н. Контроль арифметических операций в системе остаточных классов.//Исследования в области естественных наук//. 2014. № 6 (30). С. 6.
- Горденко Д.В., Кондрашов А.В. Обнаружение и коррекция ошибок в арифметических операциях.// Исследования в области естественных наук//. 2014. № 7 (31). С. 25-30.
- Горденко Д.В., Кондрашов А.В., Дорошев А.В. контроль арифметических операций на основе применения AN-кодов. //Исследования в области естественных наук//. 2014. № 11 (35). С. 47-50.


