Введение
Вертикальный профиль скорости звука – один из основных гидрофизических параметров, важный для прогнозирования условий работы корабельных гидроакустических средств, точного определения глубин и составления карт рельефа морского дна и т.д. [1]. Значения этого профиля (гидрологические условия) в значительной мере определяют рефракцию акустических волн, так что экспериментальное определение указанных профилей важно для многих задач гидрометеорологического обеспечения деятельности подводных лодок и средств противолодочной обороны [2, 3].
В настоящее время для определения вертикальных профилей скорости звука используется два подхода. Первый из них состоит в том, что с помощью соответствующих контактных датчиков, (установленных, например, на батитермографических буях) определяется температура воды на различных глубинах. Затем по известным температуре, давлению и солености морской воды, исходя из соответствующих эмпирических зависимостей, вычисляется искомый профиль скорости звука. Однако это достаточно долгая процедура. Кроме того, при определенных условиях необходимо периодически «поверять» указанную эмпирическую зависимость [1].
Поэтому определенное распространение получил и второй подход, основанный на измерении непосредственно градиента скорости звука с помощью перемещаемого по глубине соответствующего прибора. В частности, профиль скорости звука может определяться штатным прибором подводной лодки при ее «экскурсии по глубине». Однако последняя процедура требует определенного времени. То есть, практическая реализация этого подхода не всегда удобна (и возможна) [4].
Определенный интерес представляет подход к зондированию, основанный на эффекте Доплера в неоднородных средах и позволяющий найти вертикальный профиль показателя преломления или профиль скорости звука [5-7]. В [6-7] этот подход рассматривался применительно к атмосфере.
В данной работе рассматриваются особенности эффекта Доплера применительно к определению вертикального профиля скорости звука в океане.
Доплеровская локация свободно погружающегося пассивного отражателя
Эффект Доплера (доплеровская локация) широко используется в измерительной технике для определения скорости V движения различных объектов. При этом неявно полагается, что известна фазовая скорость волны C. Однако если в среде имеются градиенты фазовой скорости волны, то возникает вопрос, какое именно значение C следует использовать при вычислении V? С другой стороны, зная V, можно, в принципе, определить и C. Анализ показывает, что эффект Доплера применительно к средам с градиентами скорости звука (показателя преломления) имеет особенность, состоящую в следующем [5-7]. На сдвиг частоты влияют лишь «локальные» значения скорости звука (показатель преломления) в окрестности движущихся источника и приемника. «Локальность» скорости волны можно определить следующим образом. Если длина волны много меньше расстояния между источником и приемником, то локальная скорость волны есть скорость, усредненная по пространственному масштабу порядка длины волны. В противном случае усреднение следует проводить по масштабу, равному указанному расстоянию.
Положим, что «неподвижное» (лежащее в дрейфе) судно находится на некоторой глубине z0 (для надводного судна z0 = 0). Установленный на судне доплеровский локатор излучает акустическую волну с несущей частотой f1 = 1/(2), модулированную «низкой» частотой f2 = 2/(2). Если h - требуемое пространственное разрешение, H - максимальная глубина измерений, то указанные частоты выбираются из следующих условий: f1 С/h (1 h); f2 C/H (2 H), где C – средняя скорость звука в исследуемой среде, 1 = C/f1, 2 = C/f2.
Эта волна направляется на некоторый пассивный отражатель, погружающийся по вертикали («тонущий» в воде) со скоростью V = dz/dt.
С практической точки зрения требования к отражателю минимальны – его эффективный поперечник рассеяния должен быть достаточным для уверенного приема отраженного (рассеянного) акустического сигнала. Таким отражателем может быть некоторый сбрасываемый с судна диск («расходный материал»), опускающийся на дно под действием собственного веса. Верхняя (обращенная к судну) поверхность диска может быть выполнена катафотной.
Для скорости звука С(z) на глубине z частоты fp1, fp2 сигналов, принятых локатором при z = 0, имеют вид:
где
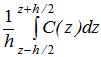 ; Cс =
; Cс =.gif) .
.Поскольку величина h соответствует пространственному разрешению, то можно принять, что Ch = C(z) есть «локальная» скорость звука. Очевидно, Cс есть средняя скорость звука (скорость, усредненная по глубине от z0 до z – z0).
Отношение C(z)/Cс не зависит от скорости V движения отражателя и определяется только вертикальным профилем скорости звука:
.gif) A =
A = .gif) . (1)
. (1)Для большинства практических задач, связанных с зондированием океана, относительные изменения скорости звука весьма малы, т.е. |A – 1| << 1. Тогда из (1) нетрудно получить дифференциальное уравнение:
Его решение имеет вид:
.gif) dz, (2)
dz, (2)где C(z0) – скорость звука на уровне z = z0, причем A(z0) = 1.
Глубина z - z0 отражателя в каждый момент времени может быть определена, например, штатным эхолотом. С другой стороны, эта глубина определяется наклонной дальностью и углом места отражателя. В свою очередь, эти характеристики могут быть измерены либо штатными судовыми средствами, либо в соответствии с методикой [6].
Оценим возможные погрешности измерений в соответствии со схемой рис. 1.
В локаторе несущая частота f1 и частота модуляции f2 формируются из опорной частоты f0 путем деления последней в требуемое число раз: f1 = f0/k1; f2 = f0/k2. Для оценок положим, что f0 108 Гц,k1 = 103 (f1 105 Гц, 1 100 см), k2 = 108 (f2 100 Гц, 2 100 км).
Для скорости движения отражателя V 1,5 м/с имеем: f1/f1 f2/f2 = 2V/C 210-3. То есть, относительные сдвиги частоты малы. Если измерять частоты принятых на судне сигналов, то затем необходимо будет найти и малую разность fi = fpi - fi двух сравнительно больших величин fpi, fi (i = 1, 2). При этом соответствующие относительные погрешности должны быть существенно меньше, чем 10-3. Однако нас интересуют лишь относительные сдвиги частоты, измерения которых можно обеспечить более простым путем.
Если принятый на судне сигнал несущей частоты fp1 смешать с сигналом «несмещенной» частоты f1, то мы получим «биения» – результирующий сигнал с частотой fp1 f1, модулированный по амплитуде частотой f1 = fp1 – f1. Измерение периода T1 этой частоты T1 = 1/f1 легко осуществить путем заполнения его метками времени с периодом опорной частоты T0 = 1/f0 и подсчета соответствующего количества N1 импульсов: T1 = N1T0.
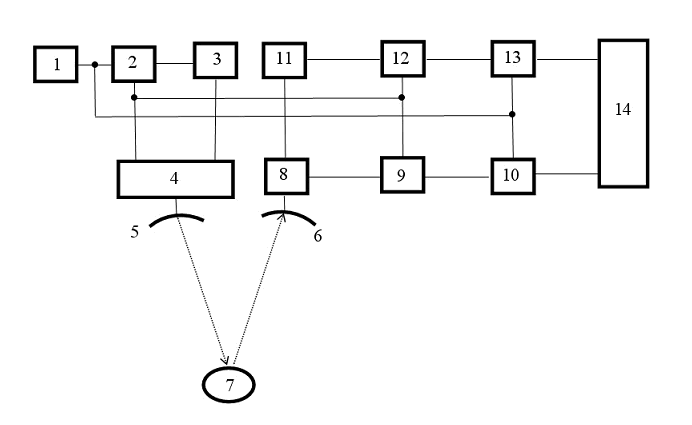
Рис. 1. Функциональная схема измерений
1 – генератор опорной частоты f0; 2 – формирователь несущей частоты f1;
3 - формирователь частоты модуляции f2; 4 – модулятор; 5 – передающая антенна;
6 – приемная антенна 7 – пассивный отражатель; 8 – блок разделения несущей частоты и частоты модуляции; 9 – смеситель (для несущей частоты); 10 – измеритель длительности периода биений несущей частоты; 11 – умножитель частоты модуляции; 12 – смеситель (для частоты модуляции); 13 – измеритель длительности периода биений частоты модуляции; 14 – блок обработки
Тогда f1/f1 = T1/T1 = k1T0/N1T0 = k1/N1. Если, как отмечалось выше, положить k1 = 103, V/C = f1/f1 10-3, то N1 106. Оценим теперь относительную погрешность измерения f1/f1:
Но f1/f1 = T1/T1 = N1/N1 + T0/T0 = N1/N1 + f0/f0.
При электронно-счетном методе измерения периода можно считать, что N1/N1 1/N1.
В рассматриваемом случае существенна лишь кратковременная относительная нестабильность опорной частоты f0/f0 – за время, существенно меньшее секунды. Поэтому такая нестабильность может быть не хуже 10-7 при сравнительно несложной электронной схеме. Частота f1 формируется путем деления опорной частоты f0. Поэтому можно считать, что относительные нестабильности этих двух частот равны: f1/f1 f0/f0 10-7.
Тогда получим:
Если, как отмечалось выше, принять, что N1 106, то (f1/f1 )/(f1/f1) 10-6.
Нетрудно видеть, что за время измерения T1 отражатель пройдет расстояние
VT1 = V/f1 = C/f1 1. То есть, и с рассматриваемой точки зрения пространственное разрешение примерно равно длине волны.
При измерении сдвига частоты модуляции исходной волны непосредственное выделение биений вряд ли перспективно, поскольку резко возрастает время измерений и резко ухудшается пространственное разрешение.
Поэтому в данном случае можно поступить следующим образом. Как отмечалось выше, частоту модуляции f2, как и несущую частоту f1, получают из опорной частоты f0 путем деления, причем f1 =f0/k1; f2 = f0/k2. То есть, f2 = f1/М, где М k2/k1 – известное число. При надлежащем выборе значений k1, k2 число М может быть целым числом (М 104 105).
Итак, частоту модуляции fp2 принятого на судне сигнала умножают на то же самое число М. Полученная частота f*p2 = Mfp2 будет очень близка к несущей частоте f1. Далее измерения проводятся аналогично измерениям на несущей частоте: при смешении «умноженной частоты модуляции» f*p2 с опорной частотой получают биения, затем выделяют период этих биений T2 и заполняют его метками времени с периодом частоты T0 = 1/f0 и подсчитывают соответствующее количество N2 импульсов: T2 = N2T0 (N2 106). В этом случае (f2/f2 )/(f2/f2) 1/N2 10-6.
Для относительной погрешности A/A получим:
A/A = (f1/f1 )/(f1/f1) + (f2/f2 )/(f2/f2) 1/N1 + 1/N2 210-6. Но A 1, поэтому
A 210-6.
С другой стороны, A – 1 C/C. Для оценок положим, что A/A C/C.
Итак, C/C 210-6; C 0,3 см/с. То есть, абсолютная погрешность определения скорости звука не превосходит 1 см/с.
Следует отметить, что при определении вертикального профиля для каждого значения скорости звука необходимо знать соответствующую глубину. Если исходить из того, что глубина z определяется обычным эхолотом, то для относительной погрешности z/z можно принять типичное значение z/z 10-2.
Качка судна и доплеровская локация
Выше неявно предполагалось, что во время измерений судно неподвижно, что качка отсутствует. Это может быть справедливым для подводной лодки, находящейся на достаточной глубине. Надводные же суда в подавляющем большинстве случаев подвержены различным видам качки – бортовой, килевой и т.д. Рассмотрим поэтому возможное влияние качки на результаты измерений.
Положим, что судно под действием качки совершает в направлении линии визирования гармонические колебания с некоторыми амплитудой X0 100 м частотой 10-2 с-1 . Тогда для несущей частоты получим:
Здесь – фаза колебаний судна под действием качки.
Поскольку f1 105 Гц, то <<< f1. При этом за характерное время порядка T1 = 1/f1 движение судна можно считать линейным. То есть, в данном случае действие качки эквивалентно изменению скорости отражателя V. Однако отражатель находится на глубине z, на которой скорость звука есть C(z), в то время как судно находится на поверхности воды (z = 0), где скорость звука есть C(z = 0) =C(0).
Для частоты модуляции имеем:
Поскольку f2 100 Гц, то << f2. При этом за характерное время порядка T1 = 1/f2 движение судна можно считать линейным. То есть, и в данном случае действие качки эквивалентно изменению скорости отражателя V. При этом в оба слагаемых входит одна и та же величина Cc - скорость звука, усредненная по глубине z.
Обозначим линейную скорость суда за счет качки через V0: V0 X0 sin(t + ). Тогда
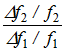 =
= .gif) .
.Нетрудно видеть, что V0 X0 10-2 м/с << V 100 м/с. При этом выражение для A можно упростить:
Отсюда получим:
Итак, при наличии качки параметр A зависит не только от интересующих нас скоростей звука C(z), Cc, но, к сожалению, и от соотношения скоростей V и V0. То есть, наличие качки приводит к дополнительным погрешностям измерения скорости звука. Если V0/V << 1, то дополнительные относительные погрешности будут иметь тот же порядок малости V0/V. Если же V0 = 0, то мы получим соотношение (1).
Для приведенных выше значений V0/V 10-2. Однако такие погрешности вряд ли приемлемы для практики. Поэтому необходимы какие-то приемы для устранения (компенсации) влияния качки.
Один из таких приемов состоит в следующем. Доплеровский локатор помимо «основной» волны, направленной на пассивный отражатель, излучает дополнительную волну с теми же частотными характеристиками, однако направленную не на отражатель, а на грунт.
Поскольку относительно грунта судно движется только за счет качки, то для частот fp10, fp20 дополнительной волны, принятых локатором при z = 0, имеем:
Если теперь на смеситель 9 (рис. 1) вместо сигнала с частотой f1 подать сигнал с частотой fp10, то результирующий сигнал «биений» с частотой f1 = fp1 – f1 будет иметь тот же вид, что и сигнал в случае отсутствия качки: f1/f1 = 2V/C(z). Аналогично, если на смеситель 12 (рис. 1) вместо опорной умноженной частоты Mf2 подать умноженную частоту Mfp20, то результирующий сигнал «биений» с частотой f2 = fp2 – f2 будет иметь тот же вид, что и сигнал в случае отсутствия качки: f2/f2 = 2V/Cс.
Таким образом, влияние качки суда на результаты измерения скорости звука может быть устранено путем определенного усложнения конструкции – введения дополнительной акустической волны, направленной на грунт с использованием смещения ее частоты для компенсации погрешностей при измерениях по основной акустической волне.
Доплеровская локация морского грунта
При наличии отражателя глубина z (отсчитываемая от уровня поверхности) определяется положением этого отражателя, причем изменение z соответствует погружению отражателя и, по сути, является непрерывным. В данном случае использование только одной частоты модуляции достаточно для корректного измерения вертикального профиля скорости звука в пределах заданной глубины.
В то же время, для многих практических задач, по-видимому, достаточной является «грубая» оценка гидрологических условий, например, выбор одного из следующих типовых случаев вертикального профиля скорости звука: отрицательная рефракция; положительная рефракция; изотермия; слой скачка скорости звука; подводный звуковой канал [1].
Рассмотрим поэтому ситуацию, когда глубина остается фактически неизменной, но при этом в измерениях используются различные частоты модуляции. Тогда при определении профиля скорости звука различные длины волн в определенном смысле соответствуют различным значениям z. По сути, имеет место определенная аналогия с доплеровским гидроакустическим лагом [8]. В этом случае полезный сигнал обусловлен отражением акустической волны от грунта. Соответственно, практическая реализация таких измерений может существенно проще, чем при использовании отражателя.
Положим, что судно движется на некоторой глубине z0 (для надводного судна z0 = 0) со скоростью Vл, а доплеровский локатор «зондирует» грунт. Излучение локатора с несущей частотой f1модулируется различными частотами f2, f3, …, fк - такими, что соответствующие длины волн 2, 3, …, к определяют требуемые глубины, по которым производится усреднение. Здесь к определяет количество частот модуляции – «точек отсчета», по которым будет производиться вычисление вертикального профиля скорости звука. Приемник локатора регистрирует «сдвинутые» частоты fp1, fp2, …, fpк.
Относительные сдвиги частот сигналов, принятых на судне, имеют вид:
где V – проекция линейной скорости Vл судна на линию визирования; V = Vлsin; – зенитный угол (угол направления акустической волны с осью OZ). Пусть hi - глубина относительно уровня z0: hi zi –z0; h0 = 0. Тогда скорость звука Ci определяется соотношением:
.gif) =
=.gif) ,
,Длина волны несущей частоты 1 101 см достаточно мала по сравнению с остальными линейными масштабами рассматриваемой задачи. Поэтому можно считать, что C1 – «местная» (локальная) скорость звука на глубине z0, C1 = C(z0). Далее, C2, C3, …, Ck - скорость звука, усредненная по трассе l2 = p22, l3 = p33,…, lk = pkk. Здесь p2, p3, …, pk – численные коэффициенты порядка единицы, определяющие фактический масштаб усреднения для данной длины волны 2, 3, …, k. Указанным трассам соответствуют глубины: h2 = l2cos, h3 = l3cos,…, h k = l kcos.
Найдем теперь отношение относительных сдвигов частоты:
Видно, что это отношение определяется только вертикальным профилем скорости звука C(z) и не зависит от скорости движения судна.
В рассматриваемом случае мы не можем определить «тонкую структуру» профиля скорости звука, поскольку имеем дело лишь со скоростями, усредненными по различным пространственным масштабам. Поэтому рассмотрим вопрос о «грубой» структуре этого профиля, о вертикальном градиенте скорости звука.
Положим, что Ai+1 - Ai A; hi+1 - hi h; Gi A/h. Тогда:
.gif) -
- .gif) }=
}= где
.gif) =
= .gif) -
- 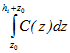 ] =
] = Здесь Ci* - скорость звука, усредненная по глубине между уровнями hi и hi+1; Ci – скорость звука, усредненная по глубине между уровнями h0 (h0 = 0) и hi. Для общности примем, что C1* = C1 =C(z0).
В определенном смысле для рассматриваемой задачи величина Gi является мерой вертикального градиента скорости звука. Отметим, что в этом же смысле Ci* может рассматриваться как мера локальной скорости звука на глубине h = (hi+1 + hi)/2.
Итак, (4) позволяет найти зависимость Gi и Ci*от глубины.
Оценим теперь возможные погрешности измерений в соответствии с (4), полагая, что hi+1 = hi = h; Ai+1 = Ai = A:
Для Gi получим:
Если измерение Ai производится по схеме, аналогичной схеме рис. 1, то для абсолютной погрешности определения A можно принять то же значение: A 10-6.
Положим для оценок, что Gi ![]() . На больших глубинах температура и соленость меняются мало, так что основной вклад в изменение скорости звука с глубиной вносит изменение гидростатического давления, причем
. На больших глубинах температура и соленость меняются мало, так что основной вклад в изменение скорости звука с глубиной вносит изменение гидростатического давления, причем![]() TS 10-5 м-1. Здесь
TS 10-5 м-1. Здесь ![]() TS – частная производная по глубине при постоянных температуре T и солености S.
TS – частная производная по глубине при постоянных температуре T и солености S.
На малых глубинах в теплых водах основной вклад в изменение скорости звука с глубиной вносит изменение температуры, причем ![]() PS 10-4… 10-3 м-1. Здесь
PS 10-4… 10-3 м-1. Здесь ![]() PS – частная производная по глубине при постоянных давлении P и солености S. То есть, для оценок можно считать, что вне области подводного звукового канала Gi 10-5… 10-3 м-1 [9]. Отметим, что в области звукового канала, где скорость звука минимальна, Gi может быть меньше приведенного выше значения 10-5 м-1.
PS – частная производная по глубине при постоянных давлении P и солености S. То есть, для оценок можно считать, что вне области подводного звукового канала Gi 10-5… 10-3 м-1 [9]. Отметим, что в области звукового канала, где скорость звука минимальна, Gi может быть меньше приведенного выше значения 10-5 м-1.
Далее, можно принять, что h 101…102 м. Тогда ![]() 10-4…10-3.
10-4…10-3.
Глубина h определяется длиной трассы усреднения скорости звука. Однако эта длина есть оценочная величина, а не измеряемая, поэтому положим, что ![]() >>
>> ![]() .
.
То есть, погрешность определения градиента скорости звука в основном определяется погрешностью h определения (оценки) глубины h:
В свою очередь, поскольку hi = pii cos, то для погрешности h = hi получим:
Поскольку глубина hi есть оценочная величина, то неясно, как эту глубину можно определить обычными способами. Тем не менее, погрешность ![]() , по-видимому, заведомо превышает погрешности
, по-видимому, заведомо превышает погрешности ![]() ; tg . Тогда имеем:
; tg . Тогда имеем:
Обоснование оценки ![]() требует проведения самостоятельных исследований. Однако «из общих соображений» представляется, что
требует проведения самостоятельных исследований. Однако «из общих соображений» представляется, что ![]() > 10-2. Тогда G/ Gi 10-1.
> 10-2. Тогда G/ Gi 10-1.
Для Ci* получим:
Положим, что ![]() 102 м;
102 м; ![]() 101; Gi 10-6… 10-4 м-1; A 10-6. Тогда
101; Gi 10-6… 10-4 м-1; A 10-6. Тогда
Как и следовало ожидать, в данном случае погрешность определения скорости звука заведомо больше, чем погрешность в случае измерений с пассивным отражателем.
Заключение
1. Рассмотрена акустическая доплеровская локация модулированными волнами свободно погружающегося в океане пассивного отражателя. Относительный сдвиг частоты зависит от скорости звука, усредненной по пространственному масштабу, определяемому длиной волны, соответствующей несущей частоте и/или частоте модуляции. Вследствие этого оказывается возможным восстановление вертикального профиля скорости звука. Для восстановления профиля скорости звука достаточно использования только одной частоты модуляции, поскольку глубина измерений возрастает за счет погружения отражателя.
Оценены возможные погрешности. При сравнительно несложном исполнении приемно-передающей аппаратуры можно обеспечить абсолютную погрешность измерений скорости звука не хуже 100см/с.
Требования к отражателю в рассматриваемом случае являются минимальными, так что этот отражатель является, по существу, «расходным материалом». То есть, рассматриваемое измерение вертикального профиля скорости звука в определенном смысле может быть названо дистанционным, не требующим никаких «контактных» датчиков.
2. Качка судна приводит к дополнительным погрешностям измерения скорости звука. Для большинства случаев эти погрешности вряд ли приемлемы для практики.
Показано, что влияние качки судна на результаты измерения скорости звука может быть устранено путем определенного усложнения конструкции – введения дополнительной акустической волны, направленной на грунт с использованием смещения ее частоты для компенсации погрешностей при измерениях по основной акустической волне.
3. Рассмотрен доплеровский гидроакустический лаг, работающий в режиме модулированных волн. При этом глубина остается неизменной фактически, но в измерениях используются различные частоты модуляции. Тогда при определении профиля скорости звука различные длины волн в определенном смысле соответствуют различным значениям глубины.
Оценены возможные погрешности. При сравнительно несложном исполнении приемно-передающей аппаратуры можно обеспечить относительную погрешность измерения вертикального градиента скорости звука не хуже 10-1.
Как и следовало ожидать, в данном случае погрешность определения скорости звука заведомо больше, чем погрешность в случае измерений с пассивным отражателем. То есть, такого рода измерения позволяют получить лишь «грубую» оценку гидрологических условий. Однако в этом случае полезный сигнал обусловлен отражением акустической волны от грунта. Соответственно, практическая реализация таких измерений может существенно проще, чем при использовании отражателя.
Библиографический список
- Серавин Г.Н. Измерение скорости звука в океане. – Л.: Гидрометеоиздат, 1979. – 136 с.
- Хвощ В.А. Тактика подводных лодок. – М.: Воениздат, 1989. – 264 с.
- Противолодочные средства иностранных флотов / Сурнин В.В., Пелевин Ю.Н., Чулков В.Л. – М.: Воениздат, 1991. – 128 с.
- Комляков В.А. Корабельные средства измерения скорости звука и моделирования акустических полей в океане. – М.: Наука, 2003. – 358 с.
- Коломиец С.М. Способ зондирования атмосферы или океана. Патент 2267139 РФ. Выдан 27 декабря 2005 г.
- Kolomiets, S.M. Sounding of ocean and atmosphere using Doppler effect in inhomogeneous media // Physics of Wave Phenomena, 2003. – Vol. 11, Number 3. – Pp. 159-167.
- Коломиец С.М. Вертикальный профиль скорости звука и конвективные движения воздуха // Исследования в области естественных наук, 2014. – № 7 [Электронный ресурс]. - URL: http://science.snauka.ru/2014/07/7631 (дата обращения: 05.08.2014).
- Абсолютные и относительные лаги / К.А. Виноградов, В. Н. Кошкарев, Б.А. Осюхин, А.А. Хребтов. – Л.: Судостроение, 1990. – 264 с.
- Андреева И.Б. Физические основы распространения звука в океане. – Л.: Гидрометеоиздат, 1975. – 192 с.


