Известно множество различных методов решения задач на соответствие между множествами, но основными являются следующие методы:
- метод рассуждений,
- метод таблиц,
- метод графов.[1]
Для облегчения решения задач выше перечисленными методами используют графические организаторы. Перечислим некоторые из них:
- таблица,
- совмещенная таблица,
- граф,
- схема
Рассмотрим применение графических организаторов при решении логических задач на соответствие между множествами.
Организатор таблица
Этот графический организатор применяется для решения двухмерных логических задач.
Задача 1. Профессии.
В небольшом городке живут пятеро друзей: Иванов, Петров, Сидоров, Гришин и Алексеев. Профессии у них разные: один- маляр, другой – мельник, третий плотник, четвертый почтальон, пятый – парикмахер. [2]
- Петров и Гришин никогда не держали в руках малярной кисти.
- Иванов и Гришин все пытаются посетить мельницу, на которой работает их товарищ.
- Петров и Иванов живут в одном доме с почтальоном.
- Иванов и Сидоров каждое воскресенье играют в городки с плотником и маляром.
- Петров брал билеты на футбол для себя и мельника.
Определите профессии каждого из друзей?
Решение.
Построим таблицу.
Таблица 1 – Незаполненная таблица
| маляр | мельник | плотник | почтальон | парикмахер | |
| Иванов | |||||
| Петров | |||||
| Сидоров | |||||
| Гришин | |||||
| Алексеев |
Из первого утверждения понятно, что Петров и Гришин не маляры. Из второго утверждения следует, что Иванов и Гришин не мельники. Из третьего утверждения получается, что Петров и Иванов не почтальоны. Из четвертого утверждения получается, что Иванов и Сидоров не маляр и не плотник. Из пятого утверждения следует, что Петров не мельник.
Решение становится очевидным, когда заполняется таблица, согласно полученным результатам.
Таблица 2 –Таблица решения
| маляр | мельник | плотник | почтальон | парикмахер | |
| Иванов | - | - | - | - | + |
| Петров | - | - | + | - | - |
| Сидоров | - | + | - | - | - |
| Гришин | - | - | - | + | - |
| Алексеев | + | - | - | - | - |
Ответ: Профессии друзей: Иванов работает парикмахером, Петров – плотником, Сидоров – мельником, Гришин – почтальоном, а Алексеев – маляром.
Организатор совмещенная таблица
При решении трехмерных логических задач на соответствие используют совмещенную таблицу, она строится из нескольких обычных таблиц.
Задача 2. Три дочери.
Три дочери писательницы Дорис Кей – Джуди, Айрис и Линда – тоже очень талантливы. Они приобрели известность в разных видах искусств – пении, балете и кино. Все они живут в разных городах, поэтому Дорис часто звонит им в Париж, Рим и Чикаго. Известно, что:
- Джуди живет не в Париже, а Линда – не в Риме;
- Парижанка не снимается в кино;
- Та, кто живет в Риме, певица;
- Линда равнодушна к балету. [3]
Решение.
Составим таблицу, в ней нужно учесть, что речь идет о трех множествах: имен, видов искусств и городов. Из первого условия можно поставить минусы на пересечении столбцов Джуди, Париж и Линда, Рим. Также можно установить из условий 1 и 3, что Линда не певица. Из условия 4 она равнодушна к балету. Следовательно, можно поставить плюс в клетке Линда, кино. После этого ясно, что кино не занимаются все остальные, расставляем минусы в таблице. Из условия 2 находим, что Линда не парижанка. В Париже может жить только Айрис (ставим плюс), минусы будут в клетках Айрис, Рим и Айрис, Чикаго. В столбце Рим уже два минуса, то есть можно установить, что там живет Джуди. И из условия 3 она певица. Оставшееся занятие: балет достается Айрис.
Таблица 3 – Совмещенная таблица
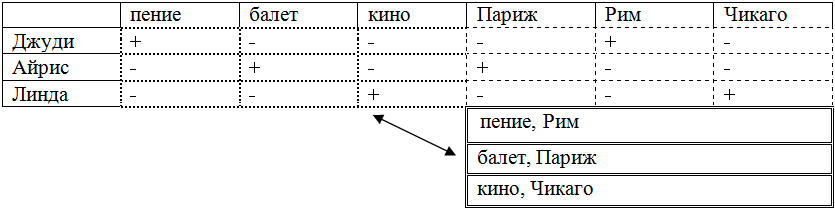
Ответ: Джуди достигла известности в пении и живет в Риме; Линда проживает в Чикаго и занимается балетом; Айрис- балет, Париж.
Организатор граф
Для решения задач на соответствие типа «Кто есть кто?» достаточно эффективно можно использовать графы. Элементы множеств обозначаются вершинами графа, а отношения между ними – ребрами графа. При этом получается k-дольный граф, где k – число множеств в задаче.
Задача 3. Соревнование по фехтованию.
Артем, Петр, Андрей участвовали в соревнованиях по шахматам и заняли первые три места. Какое место занял каждый из них, если Петр занял не второе и не третье, а Андрей не третье?
Решение.
Пусть вершины первой доли графа – имена шахматистов, а вершины второй доли – места, которые они заняли.
Введем обозначения:
![]()
По условию задачи, сразу можно сделать вывод, что Петр занял первое место. Следовательно, Андрей занял второе, а Артем – третье место.

Ответ: Петр – первое место, Андрей- второе место, Артем- третье место.
Организатор схема
Для решения логических задач на соответствие также используют такой графический организатор, как схема. Она дает наглядность и простоту решения задачи, но в то же время она дает уверенности в правильности решения.
Задача 4. Сосуды.
В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке; сосуд с лимонадом стоит между кувшином и сосудом с квасом; в банке не лимонад и не вода; стакан стоит между банкой и сосудом с молоком. В каком сосуде находится каждая из жидкостей? [4]
Решение.
Введем обозначения:
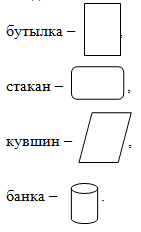
1) Так как вода и молоко находятся не в бутылке, следовательно, в бутылке квас или лимонад.
2) В банке находится не лимонад и не вода, следовательно, в банке квас или молоко
3) Сосуд с лимонадом стоит между кувшином и сосудом с квасом, значит, в кувшине находится не лимонад и не квас, следовательно, там молоко или вода
4) Стакан стоит около банки и сосуда с молоком, следовательно, в стакане не молоко, а в банке может находиться молоко, а в стакане может находиться квас, лимонад или вода

5) Из пунктов 2) и 4) получается, что в банке налито молоко.

6) Из пунктов 3) и 5) получается, что в кувшине вода

7) Если бутылка с квасом или лимонадом находится между кувшином с водой и стаканом с квасом, то получается, что в стакане находится квас.

8) Следовательно, лимонад находится в бутылке.
Ответ: Молоко – в банке; квас – в стакане; лимонад – в бутылке; вода – в кувшине.
В заключение отметим, что решение приведённых задач возможно и без графических организаторов. Можно попытаться просто строить рассуждения, решать методом перебора. Однако использование графических организаторов значительно упрощает решение, даёт ясность, чёткость, строгость, а, следовательно, и уверенность в правильности полученного ответа задачи.
Библиографический список
- Сангалова М.Е. Курс лекций по математической логике. – Арзамас: Арзамас. гос. пед. ин-т, 2006. 98 с.
- В помощь школьнику. URL: http://booklisting.ru/resheniya-po-predmetam/informatika/v-gorode-zhivut-5-druzej-ivanov-petrov-sidorov-grishin-alekseev-proffessii-u-nix-raznye-odin-iz-nix-malyar-vtoroj-melnik-3-plotnik-4-pochtalon-5-par/ (дата обращения 22.05.2014 г.).
- Электронный образовательный ресурс по “Информатике и ИКТ”. URL: http://mir-logiki.ru/log_zadachi_tren (дата обращения 28.05.2014 г.).
- Narva Vocational Training Centre. URL: http://nvtc.ee/e-oppe/Sidorova/kursus/logic8/__3.html (дата обращения 30.05.2014).


