При разработке вычислительных средств, функционирующих в системе остаточных классов (СОК) возникает важная задача обеспечения достоверности всего потока информации. Обеспечение достоверности всего потока информации прямо и непосредственно связано с увеличением производительности вычислительных машин. Для каждого специального кода, обладающего способностью к обнаружению и коррекции ошибки, характерно наличие двух групп цифр – информационной и контрольной. В информационную группу входят цифры, составляющие числовое значение закодированной величины, а в контрольную – цифры, дополнительно вводимые для целей обнаружения и коррекции возможных искажений.
В настоящее время СОК привлекает все более пристальное внимание из – за ее способности поддерживать высокоскоростную арифметику при параллельной обработки данных.
Система остаточных классов представляет собой такую систему, в которой целое положительное число представляется в виде набора остатков по выбранным основаниям [1]
А = (a1, a2,…, an), an
º
А (mod pn), n = 1, 2,…, k, (1)
где pn – основания системы остаточных классов.
Корректирующие свойства кодов в остатках, как и любого другого кода, проявляется при введении избыточности. Пусть число А представлено остатками a1, a2,…, an по основаниям p1, p2,…, pn. Диапазон представления чисел по выбранным основаниям равен произведению этих оснований, его обозначим как
R = 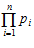 , (2)
, (2)
где R – рабочий диапазон системы.
Введем основание pn+1, и будем представлять числа в системе из n+1 оснований. Это означает, что будем передавать числа и производить операции над числами, лежащими не в диапазоне [0, R), а в более широком диапазоне [0, P).
P = R× pn+1,
где P– полный диапазон системы с одним контрольным основанием. Если в результате, какой – либо операции или при передаче числа оказалось, что получено число А>R, то значит, при проведении операции была допущена ошибка.
Таким образом, для того чтобы обнаружить наличие или отсутствие ошибки в числе А, надо сопоставить его с диапазоном R. При этом если оказалось А
³
R, значит, имела место ошибка, по крайней мере, в одной цифре. Если же А < R, то либо ошибки нет, либо она носит более сложный характер. Будем в дальнейшем числа, меньшие R, называть правильными, а большие R – неправильными.
Пусть основания p1, p2,…, pn, pn+1 системы остаточных классов удовлетворяют условию
pi< pn+1
где i = 1, 2, …, n, и пусть А = (a1, a2,…, ai ,…, an, an+1) – правильное число. Тогда величина A не изменится, если будем представлять его в системе оснований, из которой изъято основание pi (т.е. если в представлении A зачеркнуть цифру ai).
Назовем число Аi, полученное из А зачеркиванием цифры ai, проекцией числа А по основанию pi.
Если в упорядоченной системе оснований
p1< p2< …< pn< pn+1
задано правильное число A, то проекции этого числа по всем основаниям совпадают, т.е.
A1 = A2 =…= Ai =…= An+1 <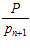 .
.
По величинам проекций можно сделать выводы о правильности отдельных цифр. Так, например, если в упорядоченной системе оснований проекция Аi числа А = (a1, a2,…, ai ,…, an, an+1) по основанию pi удовлетворяет условию
Ai >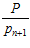 , (3)
, (3)
то цифра ai правильная, если возможна ошибка по одному какому – либо основанию. Если же (3) имеет место для всех i = 1, 2, …, n, то ошибочна цифра an+1.
Введение только одного контрольного основания не позволяет в общем случае локализовать ошибочный разряд. Коды с двумя контрольными основаниями обладают большими обнаруживающими и корректирующими возможностями. Таким образом, дополнении к рассмотренной выше системе оснований добавляем основание pn+2
> pn+1
p1, p2,…, pn, pn+1, pn+2
и будем представлять числа, лежащие в рабочем диапазоне [0, R), в системе имеющей диапазон [0, P), где
P= R×
pn+1× pn+2.
Если в системе p1, p2,…, pn, pn+1, pn+2 с двумя контрольными основаниями задано неправильное число 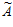 = (
= (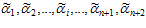 ), то необходимым и достаточным условием ошибочности цифры
), то необходимым и достаточным условием ошибочности цифры 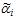 в
в 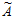 является правильность его проекции
является правильность его проекции 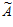 i по основанию pi. Из этого вытекает следующий алгоритм определения ошибочной цифры. Вычисляются проекции числа
i по основанию pi. Из этого вытекает следующий алгоритм определения ошибочной цифры. Вычисляются проекции числа 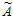 по всем основаниям
по всем основаниям
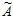 1,
1, 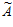 2,…,
2,…, 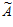 i,…,
i,…, 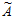 n+2.
n+2.
Среди этих проекций есть одна 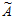 i <
i < 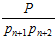 . Тогда ошибочной является цифра
. Тогда ошибочной является цифра 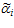 .
.
Заметим, что данный алгоритм, может быть, применим для нахождения и исправления не только одиночной ошибки, но и при некоторых условиях также двойных и тройных ошибок.
Обработка информации, основанная на параллелизме и модульности СОК, служит идеальной основой для разработки довольно значительного набора методов повышения отказоустойчивости вычислительных средств. С повышением интереса к машинной арифметики в СОК возникла возможность построения кодов обнаруживающих и исправляющих ошибки с применением нейронной сети (НС).
Нейронная сеть является совокупностью элементов (нейронов), соединенных некоторым образом так, чтобы между ними обеспечивалось взаимодействие и представляет собой высокопараллельную динамическую систему [2]. Проблема исследования надежности нейронных сетей находится еще в самом начале своего развития. Ее решение окажет значительное воздействие на реализацию нейрокомпьютеров (НК) построенных по новым технологиям. Структура нейронных ЭВМ представляет собой массив процессоров. Это предъявляет особые требования к процедуре диагностики по крайней мере той части нейронных ЭВМ, которая представляет сеть нейронов.
В статье представлен алгоритм локализации ошибок методом проекции числа в СОК по каждому из оснований на основе НС. Такая сеть будет представлять собой НС конечного кольца (НСКК) и пороговую функцию активации (рис. 1).
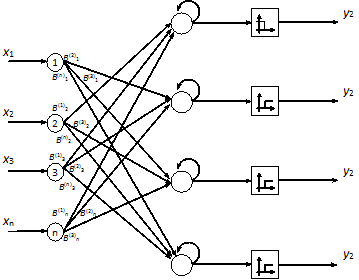
Рисунок 1 – Нейронная сеть, обеспечивающая метод проекций в СОК
НСКК состоит из сборного и вычислительного слоев [3]. Сборный слой используется для сбора входов, принадлежащих одному двоичному разряду входных источников. Вычислительный слой реализует вычислительную модель
На этапе настройки сети устанавливаются следующие значения весов
Wi=Bi, где Bi – ортогональные базисы СОК. Функция активации представляет собой порог (рис. 2).
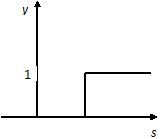
Рисунок 2 – Пороговая функция активации
Если применяется пороговая функция активации, то выходное значение нейронного элемента [4]
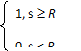
y =
Таким образом, НС локализует ошибку в данных, представленных в СОК с основаниями p1, p2,…, pn, pn+1, pn+2, по значению проекций числа A. Если на выходе нейронной сети «1» – ошибка по данному основанию, «0» – ошибки нет.
Из сказанного выше хорошо видно, что существующие разработки по теории СОК обеспечивают реальную возможность повышения информационной надежности вычислительной системы. Это обусловлено специфическими способностями представления и обработки непозиционных кодовых структур в СОК [5]. Следовательно, внедрение чисел в модулярном коде, является одним из наиболее перспективных путей повышения отказоустойчивости и быстродействия вычислительных средств.
Для иллюстрации рассмотренного метода проекции числа в СОК по каждому из оснований приведем пример.
Выберем систему p1=2, p2=3, p3=5, p4=7, для которой диапазон правильных величин (рабочий диапазон) R=2×3×5×7=210. Введем контрольные основания p5=11, p6=13. Тогда полный диапазон определяется как: P=210×11×13=30030.
Вычислим ортогональные базисы этой системы:
В1=15015, В2=20020, В3=6006, В4=25740, В5=16380 В6=6930.
Пример. Передано число А= (1, 2, 2, 3, 6, 4) = 17. Принято вместо него число 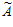 = (1, 2, 2, 3, 1, 4). Вычисляем величину
= (1, 2, 2, 3, 1, 4). Вычисляем величину 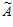 :
:
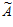 = 1×15015+2×20020+2×6006+3×25740+1×16380+4×6930 – r×30030==8207.
= 1×15015+2×20020+2×6006+3×25740+1×16380+4×6930 – r×30030==8207.
Неравенство 8207 > 210 устанавливает, что 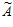 неправильное.
неправильное.
Вычислим проекции числа 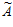 по каждому из оснований.
по каждому из оснований.
По основанию p1=2.
Для системы с основаниями: p2=3, p3=5, p4=7, p5=11, p6=13 вычислим ортогональные базисы В(1)2=5005, В(1)3=6006, В(1)4=10725, В(1)5=1365, В(1)6=6930.
Тогда
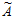 1= (2, 2, 3, 1, 4)= 2×5005+2×6006+3×10725+1×1365+4×6930 – r1×15015= =8207>210.
1= (2, 2, 3, 1, 4)= 2×5005+2×6006+3×10725+1×1365+4×6930 – r1×15015= =8207>210.
По основанию p2=3.
Для системы с основаниями: p1=2, p3=5, p4=7, p5=11, p6=13 вычислим ортогональные базисы В(2)1=5005, В(2)3=6006, В(2)4=5720, В(2)5=6370, В(2)6=6930.
Тогда
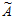 2= (1, 2, 3, 1, 4)= 1×5005+2×6006+3×5720+1×6370+4×6930 – r2×10010= =8207>210.
2= (1, 2, 3, 1, 4)= 1×5005+2×6006+3×5720+1×6370+4×6930 – r2×10010= =8207>210.
По основанию p3=5.
Для системы с основаниями: p1=2, p2=3, p4=7, p5=11, p6=13 вычислим ортогональные базисы В(3)1=3003, В(3)2=2002, В(3)4=1716, В(3)5=4368, В(3)6=924.
Тогда
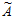 3= (1, 2, 3, 1, 4)= 1×3003+2×2002+3×1716+1×4368+4×924 – r3×6006= =2201>210.
3= (1, 2, 3, 1, 4)= 1×3003+2×2002+3×1716+1×4368+4×924 – r3×6006= =2201>210.
По основанию p4=7.
Для системы с основаниями: p1=2, p2=3, p3=5, p5=11, p6=13 вычислим ортогональные базисы В(4)1=2145, В(4)2=2860, В(4)3=1716, В(4)5=3510, В(4)6=2640.
Тогда
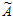 4= (1, 2, 2, 1, 4)= 1×2145+2×2860+2×1716+1×3510+4×2640 – r4×4290= =3917>210.
4= (1, 2, 2, 1, 4)= 1×2145+2×2860+2×1716+1×3510+4×2640 – r4×4290= =3917>210.
По основанию p5=11.
Для системы с основаниями: p1=2, p2=3, p3=5, p4=7, p6=13 вычислим ортогональные базисы В(5)1=1365, В(5)2=910, В(5)3=546, В(5)4=1170, В(5)6=1470.
Тогда
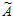 5= (1, 2, 2, 3, 4)= 1×1365+2×910+2×546+3×1170+4×1470 – r5×2730= 17<210.
5= (1, 2, 2, 3, 4)= 1×1365+2×910+2×546+3×1170+4×1470 – r5×2730= 17<210.
По основанию p6=13.
Для системы с основаниями: p1=2, p2=3, p3=5, p4=7, p5=11 вычислим ортогональные базисы В(6)1=1155, В(6)2=1540, В(6)3=1386, В(6)4=330, В(6)5=210.
Тогда
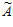 6= (1, 2, 2, 3, 1)= 1×1155+2×1540+2×1386+3×330+1×210 – r6×2310= =1277>210.
6= (1, 2, 2, 3, 1)= 1×1155+2×1540+2×1386+3×330+1×210 – r6×2310= =1277>210.
Итак, все проекции числа 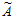 , кроме
, кроме 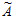 5 неправильны. Следовательно, ошибочна цифра a5=1 по основанию p5=11.
5 неправильны. Следовательно, ошибочна цифра a5=1 по основанию p5=11.
Представленный алгоритм локализации ошибок методом проекции числа в СОК по каждому из оснований на основе НС может быть, применим для локализации не только одиночной ошибки, но и при некоторых условиях также двойных и тройных ошибок, обеспечивает реальную возможность повышения информационной надежности НК. Это обусловлено специфическими способностями представления и обработки непозиционных кодовых структур в СОК.
Библиографический список
- Червяков Н. И., Горденко Д. В. Нейронная сеть для округления и масштабирования чисел, представленных в системе остаточных классов // Патент на изобретение rus 2271570 26.05.2003.
- Червяков Н. И., Сивоплясов Д. В., Горденко Д. В. Нейронная сеть для преобразования полиадического кода в код системы остаточных классов // Нейрокомпьютеры: разработка, применение. 2003. № 10-11. с. 10.
- Горденко Д. В., Горденко Н. В. Локализация ошибок в устройствах цифровой обработки сигналов на основе алгебры полиномов // Вестник Сев-Кав ГТИ. 2009. № 9. с. 56-61.
- Горденко Д. В., Резеньков Д. Н., Яйлаханов С. В. Высоконадежные комплексы и средства связи на нейросетевых элементах. Москва, 2010.
- Горденко Д. В., Горденко Н. В., Павленко Н. А., Павлюк Д. Н., Ткачук Р. В. Коррекция ошибок в системе остаточных классов с минимальной временной сложностью на основе метода расширения оснований // Известия высших учебных заведений. Северо-Кавказский регион. Серия: технические науки. 2007. № 4. с. 12-14.


