Известно что египетские пирамиды ,да и многие сооружения древности складывались из блоков, имеющих строго квадратную форму. На старинных пиктограммах и графических рисунков древности часто изображалась фигура в виде квадратной матрицы и диагонали, причем изображались вектора(стрелки ) различных длин.
Это движение объекта(движущейся точки) по косой траектории. Взлет по диагонали матрицы с левой точки (нижняя позиция) к правой точки(верхняя позиция).Спуск вниз наоборот.
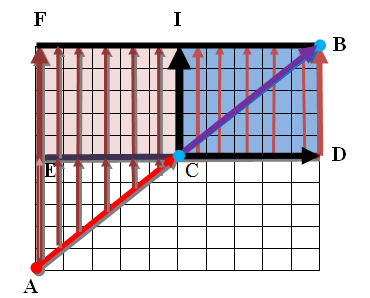
Рисунок1-изображение взлета и посадки «летающей колесницы».
Квадратная матрица – египетский ребус. Он изображается таким образом:
Рисунок 2-Египетский ребус.
Итак, движение происходит от точки А до точки В.
Задающие условия следующие:
1) В поле длины проекционного вектора, главной является крайняя нижняя точка.
2) Вектор от движущейся точки по диагонали(переход в каждый следующий квадрат) должен проецироваться на две проекционные линии (плоскости) ближнюю и дальнюю :линию ED и FB соответственно.
В этих условиях заключается правило уменьшения квадрата.
В первую половину движения имеем дело с полными длинами векторов-( вертикальное измерение расстояния; дальняя и ближняя линии (плоскости)-ED и FB являются границами отсчета проекций на ординату квадрата . Они уменьшаются по закону регрессии. Проекционные линии ED и FB вверху. Вектора исходящие из диагональной линии проходят сквозь первую среду ED ,как бы сливаясь с последующим вектором и следуют до проекционной линии FB.
Особая линия в матрице CI.Она особо важная. Здесь евклидово расстояние проекции-вертикали вектора движения на ближнюю линию ED равна нулю-то есть происходит векторная конъюнкция с ближней линией(плоскостью) ED.
И вот теперь движение по диагонали матрицы переходит в свою вторую стадию. Линия ED становится внизу нашего движения по диагонали. По условию нижняя точка является функциональной(главной),далее производные линии. Не имея возможность миновать двойную проекцию на линии ED и FB,диагональ и соответственно движущаяся точка претерпевают переход в инвариантность, и движение как бы «нащупывается» внутри уменьшенного масштаба. Одновременно с движением точки происходит прогрессия векторной проекции – увеличение длин векторов от линии абсциссы CD до собственно диагонали. В крайней точки вектор движения и проекции соединяются в точку B.
Правило уменьшения квадрата ,есть секрет матрицы, «тайный узор» или «выступ» в египетских пирамидах. Такую фигуру использовали при строительстве египетских пирамид. Она называлась египетским ребусом или «танец с тенью».[1,2]
Древние считали, что в таком ключе осуществляется переход энергий и даже тип нашего мышления починяется законам такого движения(собственно движение(субъективное) и сложенное от сторонних объектов (объективное). Переходы в разномасштабность незаметны для человека, так как это естественный факт повседневного бытия.
На этом основывались теории переходов в иные миры.
Древние маги Вавилона называли такое движение по матрице «След рыбо-птицы». Сначала это мифическое животное –рыба и как бы выныривает из глубины, а затем летит превратившись в птицу.[2,3]
Рисунки3,4,5-древние изображения мифического животного «рыбоптица».
Астрологи древности считали ,что Землю посещали летающие корабли. Большие светила (спутники, такие как например Луна и пр.) должны служить для отслеживания полетов «богов»на звезды (это означает ,что плоскость CD-зона спутников ).Выбравшись за планетарную зону, корабли становятся как бы нарисованными на пергаменте (то есть переходят в двумерное пространство) и перейдя в другой масштаб имеют сверхскорость (скорость двумерных объектов).А первая половина движения (выныривание) более тяжелая, так как имеет всю длину векторов и посему имеет объем(то есть трехмерную составляющую).
Древние ученые Византии считали, что жизнь и смерть человека связана с полетом от звезды к звезде. Человек рождается и живет по времени полета от звезды А к звезде В.Умирая он так же живет ,но в другом мире и по времени полета от звезды В к звезде А.Если жизнь его трагически обрывается, то по схеме египетской диагональной матрицы он все равно долетает до звезды В. А затем начинает свою жизнь снова совершая обратный полет.[2,3]
Рисунок 6-Временная линия жизни человека в двух мирах(изображение в древних письменах).
В современных условиях египетский ребус приобретает все более важное значение. При изначально задающих условиях движение по прямой диагонали квадратной матрицы, с обязательными условиями двойной проекции снизу вверх, компьютер автоматически будет выписывать фигуру египетского ребуса, отмечая разномасштабность движения и на этом будет основываться навигационная и локационная системы при движении вверх.
Существует целая система правил(прямой и обратной зависимостей),составляющих движения по диагонали квадратной матрицы снизу вверх, слева направо. .Например такие:
-Линии исходящие от диагонали- суть «обзора» длин пути(переменные ординаты -из терминов древних-«вертикальные столбы»[2].
-Двойная проекция – проецируется сначала ближняя линия (плоскость) ED, затем дальняя линия(плоскость) FD.
-По мере движения по диагонали в египетском ребусе проекционные линии ординаты(вектора) в первой половине пути уменьшаются во второй половине пути увеличиваются.
-При движении от нижней левой точки до верхней правой по диагонали квадрата и проецированию на ближнюю линию (средняя горизонтальная линия квадрата), нулевая вертикаль проекции (длина ординаты от движущейся точки по диагонали в точке С на ED и соответственно евклидово расстояние = 0) будет в середине квадрата.
-При движении по диагонали матрицы 1-ая половина пути собирает двойную проекцию(сдвоенные длины векторов),2-ая половина пути одинарные проекции и уменьшение квадрата.
-Векторная конъюнкция исходящая от диагонали (переменная ось ординат) с прямой линией (плоскостью) абсцисс(ближняя линия) дает свободное прохождение вектора до дальней линии(плоскости)-края квадрата в 1-ой половине пути ,а во 2-ой половине пути движение по диагонали идет между ближней и дальней линией(плоскости) и двойная проекция проходит через конъюнкцию проекционных векторов-ординат с диагональной линией(всегда пересекает диагональ).
-Двигаясь по египетскому квадрату сначала ближняя линия(плоскость)вверху, затем пройдя через грань перехода в другой узор матрицы ближняя линия становится внизу.
-При позиции ближняя проекционная линия внизу(вторая половина движения) произойдет масштабная инвариантность, то есть сокращение масштаба в 4 раза, в результате вырисовывается другой узор, другой фокус движения по диагонали квадратной матрицы.
- При условии, что ближняя проекционная линия внизу(вторая половина движения) и изменился узор матрицы и вектора, исходящие из проекционной линии (плоскости) ED вектора становятся главными, функционально направляющими .
Значки взлета по матрице по косой траектории(из древних изображений).
Рисунок 7,8,9 -Типовые обозначения, встречающиеся в трудах древних ученых.
По утверждению древних свет исходящий от заходящего или восходящего солнца-(30о над горизонтом )всегда высвечивает на небесах «обетованные знамения»(то есть самые необычные и плохо объяснимые атмосферные и иные явления).Имея источник света испускающий лучи по косой линии(аналог диагонали)мы сталкиваемся с тем же движением по египетскому ребусу и можем наблюдать невидимые до этого момента светящиеся объекты, летящие аппараты и т. д., что говорит о том, что все они находятся в так называемом «выступе» или ином масштабе египетского ребуса.
Таким образом мы рассмотрели интересное свойство матрицы и открыли секрет перехода в другой масштаб.
Письмена древних мыслителей-передовых умов прошлого, еще откроют множество знаний для человечества.
Библиографический список
- Большая Советская энциклопедия;М:,Энциклопедия,1985.
- Древние мыслители ; М:,Издательский дом «Москва- наука»,2006.
- Труды ученых Древности; Древняя Греция, Китай и пр.;М:, Дом Книги, 2005