Со времен Ньютона было ясно, что гравитационная энергия космического объекта, например, звезды, максимальна, если массу по кусочкам разнести на бесконечно большое расстояние. За гравитационную энергию принималась величина равная работе необходимой для того, чтобы разнести массу на бесконечно большое расстояние. Для того чтобы показать, что гравитационная энергия уменьшается при сжатии, был введен знак минус. Хотя, по сути, вычислялась работа выполненная силами гравитации по сжатию объекта массой М до радиуса R. К тому же при сжатии объектов увеличивались силы гравитации, что создавало впечатления роста и гравитационной энергии.

Однако, после того как стало ясно, что электромагнитные и гравитационные взаимодействия передаются с конечной скоростью, а масса эквивалентна энергии, необходимо было пересмотреть и формулу гравитационной энергии.

    Допустим, что две материальные точки массами m , движутся из бесконечности навстречу под действием сил гравитации. В данном случае гравитационная энергия переходит в кинетическую, то максимальную скорость, которую могут развить массы, не может превышать скорости передачи взаимодействия, т.е. скорости света c , то и максимальная возможная энергия гравитации системы равна (В распоряжении системы массой м, находящейся в покое , максимальная энергия равна E = m*c² ):

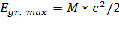
Где М – масса системы.

Тогда гравитационная энергия на любой момент времени, когда материальные точки разделяет расстояние r или космический объект массой М имеет радиус r:

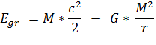
Где с – скорость взаимодействия

G – гравитационная постоянная.

Для не релятивистских объектов гравитационную энергию можно вычислить по приблизительной формуле (второй член уравнения значительно меньше первого):

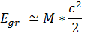
Если мы желаем вычислить изменение гравитационной энергии объекта (допустим, звезды) из состояния с начальными параметрами массой M₀ и радиусом r₀ , до состояния с конечными параметрами: массой M_k , а радиусом r_k, то формула будет выглядеть:

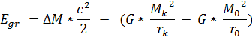
Где 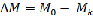– масса потерянная звездой.

Работа A_grav выполненная силами гравитации по сжатию космического объекта, когда масса М имеет характерный размер r, равна разнице между максимально возможной энергией гравитации и гравитационной энергией на данное состояние:

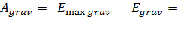
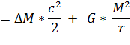
Обращает на себя внимание то, что выполненная работа силами гравитации имеет две составляющие. Первый член правой части уравнения говорит о потери массы космическим объектом при сжатии на излучение, а также звездный ветер и другие безвозвратные потери массы. Второй, член отвечает за увеличение внутренней энергии. Коэффициент одна вторая перед первым членом правой части уравнения говорит о том, что лишь половина гравитационной энергии при сжатии объекта уходит на излучение, вторая часть идет на разогрев объекта. Это верно для стационарных объектов, к которым можно условно причислить и звезды. Собственно говоря – это теорема о вириале. Удвоенная кинетическая энергия равна потенциальной энергии. Выполненную работу силами гравитации можно записать и так:

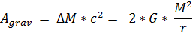
Но надо уточнить, что в данном случае речь идет не об энергии, а выполненной работой силами гравитации по сжатию космического объекта.

Поскольку во втором члене правой части уравнения конечная масса (а, не начальная М₀) ,то первый член уравнения правой части (его не нужно умножать на два) уравнения равен второму.

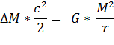
Даже если у звезды начинаются ядерные реакции, эта формула приблизительно сохраняется:

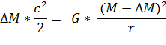
Гравитационная энергия в данном случае уменьшается за счет потери массы,

если ядерная энергия затрачивается больше на разогрев, чем теряется безвозвратно в пространстве, то в этом случае растет радиус звезды.

Член уравнения 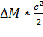связан с излучением объекта. А, мы знаем, что чем выше частота излучения , тем больше потери массы:

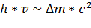
где h – постоянная Планка.

Поэтому можно записать:

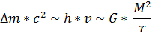
Из этой записи можно сделать вывод о том, что чем больше масса звезды и чем меньше её радиус, тем частотный диапазон излучения более смещается в жесткую сторону, а также увеличиваются потери массы на излучение. Данная зависимость хорошо объясняет диаграмму Герцшпрунга-Рессела, зависимости спектрального класса звезды от абсолютной звездной величины.

Еще о чем говорит этот комплекс формул?

Первое: о том, что масса звезды может быть сколь угодно большой, ведь гравитационная энергия пропорциональна первой степени массы. Что и наблюдается. Что касается эволюции Вселенной, то данная формула гравитационной энергии не допускает состояния сингулярности, т.е. состояния большой плотности и размеров меньше гравитационного радиуса. Зато возможен вариант со сверхзвездой. Так как гравитационная энергия пропорциональна массе, то возможно, что до взрыва Вселенная представляла собой огромной массы и радиуса сверхзвезду.

Второе: эволюция звезд идет в направлении от звезд главной последовательности, далее к красным гигантам, далее к белым карликам и в конце эволюции могут дойти до стадии нейтронных звезд. Переход от звезды главной последовательности в белый карлик и далее в течение нескольких дней в нейтронную звезду происходит при взрывах сверхновых 2-го типа.

Третье, что так называемые «Черные дыры» существовать не могут, ввиду того, что по достижению гравитационного радиуса вся масса испариться, да для достижения этого состояния гравитационной энергии не достаточно.

Из формулы гравитационной энергии видно, что её меньше, чем энергии эквивалентной массы. Именно с массой борется гравитационная энергия, превращая её в излучение.

Обращает на себя внимание следующее обстоятельство, если в формуле гравитационного взаимодействия (для простоты допустим, что взаимодействуют два тела одинаковой массы)

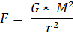
вместо радиуса (расстояния между телами) подставить формулу гравитационного радиуса

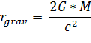
То получится не зависимость силы взаимодействия от массы, а конкретное число

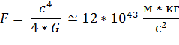
Это можно интерпретировать следующим образом, «Черную дыру» надо рассматривать не как объект, а как критическое состояние материи, при котором в качестве вещества она существовать не может, хотя формально формула гравитационного радиуса описывает объект.

Все статьи автора «Чиняков Георгий Юрьевич»