В 2002 году материал был опубликован частично в книге: Владимер Комлев «Явь и Навь, человеческие и мировые» и в том же году теория элементарных частиц была доложена на Международной конференциях «Пространство, Время, Тяготение» на
VII 2002,затем на V111 и IX конференциях, 2004, 2006 г.г. опубликовано в Сборниках конференций, СПб., «ТЕССА», 2003, 2005, 2007)

Ниже с небольшими сокращениями приведена статья, полный текст на сайте: http://vladimerkomlev.snauka.ru/

В связи с высказанными выше предположениями фотон как отдельный квант электромагнитного излучения может представлять собой незатухающие поперечные колебания разноимённых кварковых зарядов в нематериальной среде из нейтральных кварков и движущийся вместе с этой средой.

Подобные колебания очень напоминают резонансные явления в электрическом колебательном контуре, с той лишь разницей, что резонансная частота в радиотехническом контуре строго определённая и зависит от физических параметров контура (в основном от индуктивности и ёмкости). Поскольку колебания в фотоне возможны в широком спектре частот, то физические параметры контура фотона (его индуктивность и ёмкость) зависят или определяются его собственной частотой.

Процесс автоколебаний в фотоне можно представить следующим образом. Разделённые силовым воздействием разноимённые дробные заряды кварков, начинают сближаться под действием кулоновской силы. Скорость их сближения неограниченно возросла бы, но увеличивающееся, по мере нарастания скорости зарядов, магнитное поле, тормозит это сближение на одной четверти периода, а на следующей – способствует разлёту кварковых зарядов в разные стороны, пока напряженность магнитного поля не уменьшится до нуля. И снова кварковые заряды начинают сближаться. При такой модели процесса напряжённости электрического и магнитного полей совпадают по фазе, что и имеет место в электромагнитной волне. И именно это совпадение фаз обеспечивает возможность автоколебаний в фотоне в широком спектре частот. В радиотехническом же контуре напряжённости электрического и магнитного полей в идеале сдвинуты на 90 градусов.

Предположим, что колебания кварков в фотоне связаны теми же соотношениями, что и колебания в радиотехническом контуре, тогда энергия, периодически сосредотачивающаяся на электрической ёмкости фотона, будет вычисляться по известной формуле.

    ,

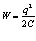где
С – условная электрическая ёмкость в системе колеблющихся кварков, q – сумма зарядов одного знака, например, кварков (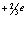). Величина q в фотоне может быть представлена одним из членов следующего ряда

    

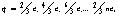
где n – число положительных кварков в фотоне, e – заряд электрона.

Приравняем энергию фотона к энергии, сосредотачиваемой на условной электрической емкости

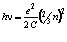    ,    (1.1)

где 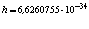Дж∙с – постоянная Планка,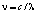
- частота фотона, с – скорость света, λ – длина волны фотона.

Значение собственной частоты автоколебаний в контуре фотона определится по известной в радиотехнике формуле для идеального контура

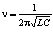    ,    (1.2)

где L – условная индуктивность в системе кварков фотона.

Подставляя значение n в формулу (1.1), получим

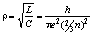    ,    (1.3)

где r – представляет собой в этом случае волновое сопротивление свободного пространства, которое вычисляется через значения магнитной mо и диэлектрической eо
постоянных этого пространства, то есть при

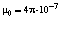     Гн/м = 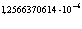Гн/м,    (1.4)

    
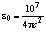
Ф/м = 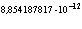Ф/м,    (1.5)

Получим

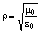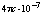     = Ом = 376,730313 Ом,     (1.6)

где с = 299792458 м/с – скорость света.

Поскольку r величина постоянная, то количество кварков в фотоне в соответствии с формулой (1.3) должно быть числом целым и неизменным при условии целостности фотона как частицы и неделимости кварков.

Итак, из формулы (1.3) находим соотношение для постоянной Планка, выраженное через волновое сопротивление свободного пространства, заряд электрона и число кварков в фотоне,

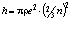    Дж с.    (1.7)

Или с учётом формулы (1.6)

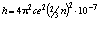    Дж∙с.    (1.7′)

Формула (1.7) позволяет вычислить количество кварков в фотоне n с зарядом (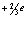) по известным значениям h, r и 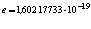K. В этом случае 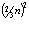= 21,809955, а n = 7,00517.

Поскольку фотон электрически нейтрален, то он содержит ещё 14,01034 кварков с зарядом (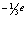). Всего в 3n = 21,01551 кварков. Отклонение значения n для положительных кварков от целого числа на величину 0,00517, возможно, связано с погрешностями определения, входящих в формулу (1.7), параметров или за этим расхождением скрывается более тонкая организация кварков фотона.

Вычислим через значения h,с и е коэффициент 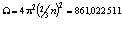    , тогда формула (1.7′) примет вид

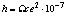    Дж·с.    (1.7”)

Известна формула, определяющая постоянную тонкой структуры 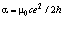 или, раскрывая μо из формулы (1.4), получим 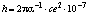Дж∙с.

Из сравнения с формулой (1.7″) при экспериментальном значении 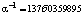, взятом из справочников, следует     .

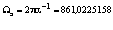Некоторое расхождение Ωэ с вычисленным ранее значением Ω вероятно связано с погрешностями в измерении α-1.

Поскольку фотон, возможно, имеет массу в движущейся совместно с ним системе координат, то есть массу «покоя», то часть энергии сосредоточена в движении этой массы. Вычислим долю энергии сосредоточенную в движении массы «покоя» фотона в предположении, что если бы фотон представлял собой идеальную замкнутую кольцеобразную структуру, а для этого воспользуемся формулой, определяющей эту массу «покоя» (вывод формулы приводится ниже)

    ,

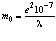где m₀ – масса «покоя» фотона.

Заменим 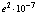на это же значение из формулы (1-7”), тогда находим

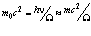    ,    (1.8)

где m – масса движущегося фотона.

В этом случае энергия hn
в формуле (1.1) должна быть меньше на величину 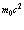, поскольку эта часть энергии не входит в энергию на электрической ёмкости, тогда

    .

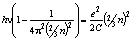Это выражение, с использованием формулы (1.2), приводится к уравнению

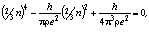        (1.9)

из решения которого, находим значение n = 7,0010955, а 3n = 21,0032865.

Однако ясно, что фотон состоит из семи целых положительных и 14 –и целых отрицательных кварков с равными суммарными зарядами с добавлением небольшой части ещё более как бы дробного заряда, вероятно связано с влиянием нейтральных участков кварковой нити. Например, ввиду конечных размеров кварков при сближении в автоколебаниях кварк 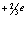«пролетает» между двумя кварками 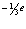как бы вытягивая из нити дополнительный заряд. Общее число целых кварков в фотоне (кванте) равно 21. Замечу, собственное число славяно-русского Триглава – три семёрки.

Из известного соотношения, связывающего рост массы частицы при увеличении скорости её движения

    ,

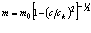при m₀ ≈ m/Ω, формула (1.8), следует, что фотон, двигаясь со скоростью с, отстаёт по скорости от скорости движения пространства нематериальных кварков ск. Поскольку это пространство разбегается в разные стороны, казалось бы, со скоростью большей скорости света примерно на величину 1,000000674 или на 202 м/с.

Если же фотон представить как поперечную деформацию расщепленного участка кварковой трассы (нити), а не идеальную кольцеобразную структуру, скорость движения кварков в которой равна скорости движения кварков свободного пространства ск, то скорость фотонов с менялась бы с изменением величины этой деформации. Однако этого не наблюдается, ск = с. Скорость фотонов действительно не будет зависеть от величины поперечной деформации, если допустить наличие пропорционального продольного сжатия этой деформации (сокращение длины фотона в направлении движения), но тогда ск 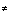 с. И в этом случае обнаружится разность скоростей.

Наиболее вероятно, что в фотоне имеют место поперечные автоколебания кваркового заряда на расщеплённых взаимно параллельных участках нейтральной кварковой нити. Нерасщеплённая нить допускает движение только со скоростью света, т.е. колеблющийся расщеплённый участок нити сохраняет движение с той же скоростью. При такой конструкции фотона вполне объяснимо то, что число кварков в фотоне чуть больше 21 ввиду частичного влияния границ расщепления. При автоколебаниях расщеплённые участки нити как бы периодически электрически упруго вытягиваются при этом не образуются какие-либо частицы. Деформация кварковых нитей, как нематериальных объектов, не приводит к каким либо энергетическим проявлениям.

Расщеплённые участки нити, несущие заряд, могут характеризоваться электрической ёмкостью и индуктивностью.

Из формулы (1.7′) подставим 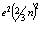в соотношение (1.1), тогда электрическая ёмкость фотона будет определяться по формуле

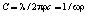    ,    (1.10)

где w = 2pν - круговая частота фотона.

Подставив значение r из формулы (1.6), получим 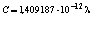    Ф.

Индуктивность фотона можно вычислить по формуле (1.3) с использованием соотношения (1.6)

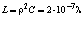    Гн.    (1.11)

Потенциал кварковых зарядов (амплитудное значение) в фотоне можно вычислить по формуле

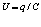    , где .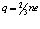

Подставляя (1.10) с учётом (1.6) при c ≈ wR, где R – максимальный размах разлёта зарядов в фотоне, получим

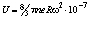    .    (1.12)

Эту формулу можно привести к виду, используя соотношения (1.6) и (1.7), то есть 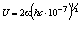    .    (1.13)

Максимальное значение энергии на индуктивности или ёмкости определится по формулам

    ,    .

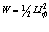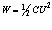Из соотношений (1.10), (1.11) и (1.12), (1.13) при амплитудном значении тока в фотоне 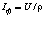получим одинаковые значения энергии на индуктивности и ёмкости, равные hn, то есть энергия, сосредоточенная на ёмкости фотона при колебательном движении эквивалентна энергии магнитного поля.

Если бы частица с массой покоя фотона могла существовать вне фотона и действительно находилась бы в покое, то её собственная (комптоновская) частота ν_ф находилась бы из формулы (1.8), после замены 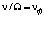, то есть     ,

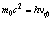где n_ф - гипотетическая комптоновская частота частицы с массой «покоя» фотона.

Энергия такой частицы (даже в случае если бы фотон представлял собой кольцеобразное образование) 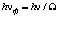равнялась бы по величине магнитной энергии на её индуктивности, то есть     .

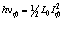Отсюда 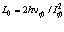    , а магнитный поток Ф при I_ф = еn вычислялся бы по формуле     ,

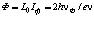а поскольку 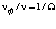, то     .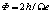

Эта величина значительно меньше кванта магнитного потока 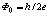, следовательно, в такой частице от тока I_ф магнитное поле не возникает и частица с массой покоя фотона существовать не может.

---

Все статьи автора «vladimerkomlev»