Спин частицы в современном представлении- это нечто иреальное даже метафизическое. [1]. Считается, что спин не поддаётся объяснению с позиций классической физики. Так ли это?

В [2]. Сообщается, что Спин — это внутренняя, исключительно квантовая характеристика, которую нельзя объяснить в рамках релятивистской механики.

В[3]. даётся физический смысл спину частицы именно как моменту ее вращения в свернутых измерениях.

Попробуем дать объяснение спина не выходя за пределы классической физики: первое представление спина в рамках классической физики дано в [4].

Собственный момент количества движения элементарных частиц M, как известно, не зависит от параметров частиц и определяется только дискретным значением спина Ј, то есть

    ,

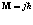где 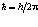, Ј – спиновое квантовое число. h- постоянная Планка.

Классический момент количества движения определяется формулой

    ,

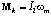где 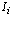– момент инерции объекта, 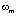– угловая скорость вращения массообразующей среды (ядре частице).

Величина 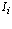зависит от формы вращающегося тела. Постоянный коэффициент при моменте инерции вращающегося кольца, как известно, равен единице, то есть

    ,

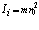где 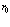– радиус вращения массообразующей среды(ядра частицы), m – масса ядра.

Подставим 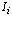в предыдущую формулу для вычисления 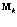и заменим 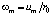, тогда

    ,

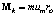где 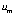– линейная скорость вращения массы кольца.

Заменим m, воспользовавшись соотношением (2.5) http://vladimerkomlev.snauka.ru/ , тогда

    .

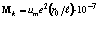Поскольку 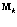и М должны быть равны, а М величина неизменная для определённой частицы, то можно записать

    .

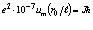Раскроем 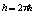из формулы (1.7′) при ℓ =2πr , r –радиус частицы тогда

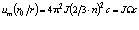    .    (3.1)

Поскольку из формулы (2.6) 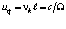, то произведение скоростей из последних формул

    .

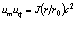Если умножить обе части последнего равенства на массу частицы, то получим соотношение для полной энергии

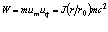    ,    (3.2)

которое приводится к соотношению для полной энергии 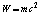при условии, что произведение спинового числа J на отношение радиуса токового кольца к радиусу массообразующего кольца равно единице, то есть, учитывая ℓ = 2πr, получим

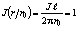    .    (3.3)

Таким образом, спиновое квантовое число частицы 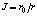характеризует отношение радиуса массообразующего кольца, которое следует назвать ядром частицы, к радиусу токового или наружного кольца. Формулу для полной энергии частицы можно получить и через момент количества движения частицы 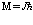, умножив его на частоту 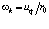, где (п. 2.4) 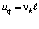, а ℓ = 2πr, то есть

    .

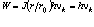В этом случае при J(r/r₀) = 1 формула (3.1) приводится к виду

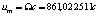    ,    (3.4)

то есть линейная скорость вращения в массообразующем кольце (ядре) частицы постоянна и в Ω раз превосходит скорость света. Вероятно именно это обстоятельство может создать эффект возникновения массы из нематериальной среды при раскручивании кольца со скоростью
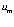
/формула (3.4)/.

Кроме того, в массообразующем кольце (ядре) присутствует ещё частота 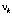и вращение с линейной скоростью 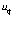/формула (2.6)/ . В этом случае отношение скоростей

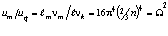    ,    (3.5)

где 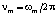– частота вращения массообразующей среды, 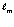– условный “классический” радиус массообразующей среды или длина образующей кольца ядра.

Из анализа формулы (3.5) можно заключить, что длины образующих колец (их классические радиусы) 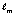и ℓ могут быть равны для частиц со спином равным единице, тогда частоты соотносятся в пропорции формулы (3.5). Раскручивание массообразующего кольца напоминает работу своеобразного электрического двигателя без нагрузки, где кольцо тока ℓ раскручивает массу m до синхронно больших частот. Если предположить, что частоты 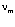и 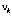равны, то размеры кольца 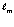, несущего массу частицы, должны превосходить размеры кольца тока ℓ в соответствии с формулой (3.5) в сотни тысяч раз. Однако это маловероятно, поскольку радиус сечения взаимодействия, например, нейтронов, не превосходит их классический радиус.

Из формулы (3.2) следует, что кольцо массы частицы с одной стороны вращается с линейной скоростью 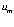значительно превышающей скорость света, с другой стороны у этого же кольца масс линейная скорость равна линейной скорости в токовом кольце 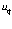. Этому, странному на первый взгляд, условию может удовлетворять следующая конструкция частицы: когда, например, вращение в ядре осуществляется в двух плоскостях.

Литература.

1. Болсун А.И., Галякевич Б.К.Физика. Краткий словарь справочник. Минск. БелЭн 1997.320 с.
2. Википедия
3. 1 А.В. Каминский “Скрытое пространство-время в физике”, Квантовая Магия, том 2, вып. 1 , стр. 1101-1125 , 2005
   
4. Милов В.А.Теория кварковых колец.Сб. Пространство,Время,Тёготение. Материалы V111 Международной конференции 16-20 августа2004г., Санкт- Петербург, Россия.СПб «ТЕССА»2005 с.179-189
   

Все статьи автора «vladimerkomlev»